下载客户端

从小玩到大的超级玛丽，计算复杂性是怎样的？

2020-08-13 14:34

来源：澎湃新闻·澎湃号·湃客

机器之心转载

作者：张诸俊

吃蘑菇长大的「超级玛丽」比你想象的更复杂。

「超级玛丽」（Super Mario Bros.）应该算是红白机上最著名的游戏了，大部分 80 后、 90 后应该都玩过吧。对于这样经典的游戏，「无聊」的游戏计算复杂性研究人员当然不会放过啦。2015 年，Aloupis, Demaine, Guo 和 Viglietta [1] 证明了「超级玛丽」属于 NP-hard。2016 年，Demaine , Viglietta 和 Williams [2] 证明了「超级玛丽」属于 PSPACE-complete。

今天我们就来详细介绍一下关于这个游戏的计算复杂性的研究。在文中我们将看到如何设置地图使得超级玛丽能够模拟一些计算困难的问题，从而说明该游戏在计算理论的角度下是难解的。

本篇的第 1 节介绍一个 NP-hard 框架；第 2 节介绍应用框架证明「超级玛丽」属于 NP-hard；第 3 节介绍一个 PSPACE-hard 框架；第 4 节介绍「超级玛丽」属于 PSPACE-hard 的归约；第 5 节说明如何使归约更完善；第 6 节进行总结。

1. NP-hard 框架

我们先来介绍一个用于证明一类 2D 游戏困难性的框架，这个框架来自文献 [1] 。我们假设在这类 2D 游戏中，玩家操控一个角色在地图上移动，玩家的目的是使该角色到达地图上的某个位置。比如 SMB 的目标就是让玛丽从出生点到达旗杆，再比如之前介绍过的华容道玩具的目标就是让特定的滑块移动到出口，再再比如 STG 游戏就是操纵可以发射子弹的角色避开敌方弹幕和地形到达关底。

框架使用的归约问题是经典的 3-SAT 问题（3-conjunctive normal form satisfiability，3 - 合取范式可满足问题）。该问题指的是给定一个由若干子句的合取构成的公式，其中每个子句包含 3 个项，判断是否存在对变量的赋值使得该公式可满足。我们希望通过使用 2D 游戏模拟 3-SAT 问题，从而将 3-SAT 归约到 2D 游戏。

我们用一个例子来说明如何进行这样的模拟。对于公式

我们可以构造如下图的 2D 游戏框架

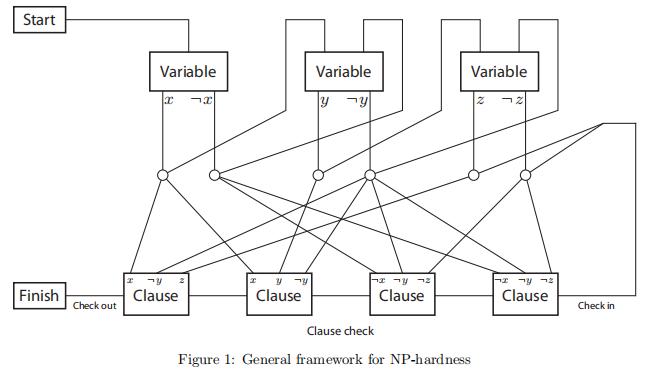
玩家操控角色从 start 部件出发，然后进入一个对应变量 x 的 variable 部件，玩家需要在两个出口之间选择一个，这模拟了对变量 x 的取值。假设选择对 x 赋值为 T，那么玩家操控的角色就从 variable 部件的左侧出口离开，接下来角色可以到达两个 clause 部件并打开这两个部件，这模拟了

和

这两个子句中的 x 为 T 后整个子句就为 T。接下来无论选择的是从 variable 部件的左侧出口还是右侧出口离开，角色都将进入到第二个 variable 部件，继续对变量 y 的赋值进行模拟。当所有变量的赋值都确定后，角色进入到验证过程（check in 路径），角色需要从右侧依次通过所有的 clause 部件才能最终达到最左侧的 finish 部件。而每个 clause 部件只有当之前角色从上方进入并打开至少一次后，才允许角色从右侧进入并通过。

为了实现这个 NP-hard 框架，我们需要在 2D 游戏中实现 5 个部件，分别是 start、finish、variable、crossover、clause，其中 crossover 部件用于处理框架中路径的交叉。容易验证，如果某个 2D 游戏能够实现这些部件，那么就能用这个游戏模拟 3-SAT 的任意实例，也就是说 3-SAT 可以归约到这个 2D 游戏，从而就说明这个游戏就属于 NP-hard 了。

不过，有时候在游戏中直接构造 variable 和 clause 部件可能会比较复杂，所以我们可以对这个框架进行一些修改，使得部件更加原子化一点。修改之后的框架含有 start、finish、turn、switch、merge、one-way、crossover、door 这些部件。start 和 finish 部件的含义与修改之前是一样的；turn 部件用于路径的转向；switch 和 merge 部件其实是同样的，通常是一个三叉路口；one-way 部件保证游戏角色只能向一个方向移动，功能类似单行道；door 部件包含两条互不连通的路径，当一条路径被角色通过后（开门），角色才能通过另一条路径。

对于公式

，对应的修改后的框架如下。

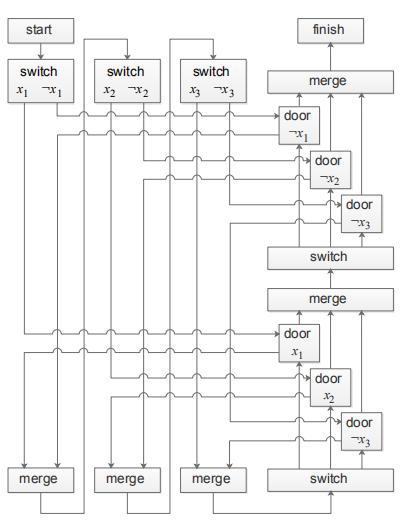
游戏角色还是从 start 部件出发，接着进入 switch 部件选择变量的赋值，赋值后可以打开对应的 door 部件，然后回到 merge 部件，接着选择下一个变量的赋值。直到所有变量的赋值被确定进入子句验证过程，角色进入右下方的 switch 部件，然后它需要在三个出口中选择一个已经被打开的 door 部件通过。当所有子句都验证完成后，角色最终进入 finish 部件。

2. 超级玛丽属于 NP-hard

我们使用上一节的框架来说明「超级玛丽」属于 NP-hard，为此我们需要在游戏中实现 start、finish、variable、crossover、clause 这些部件，我们逐一进行说明。

start 部件：玛丽的出生点有一个蘑菇，吃了之后可以变成大玛丽。

finish 部件：需要以大玛丽的状态从左下方进入部件，撞掉一个砖块后才能到达旗杆；如果以小玛丽的状态进入则不能通关。

variable 部件：玛丽从上方进入部件后，可以在左下和右下两个出口中选择，一旦决定后就不能再返回了。

crossover 部件：该部件中有两条交叉的路径，第一条由左上至右上，第二条由左下至中间上方。在第一条路径中，大玛丽进入后需要碰一下怪物变成小玛丽后才能通过狭小的通道，注意右上方的问号方块中有一个蘑菇，玛丽吃了后可以变回大玛丽状态。在第二条路径中，玛丽达到底部后一路向上，注意由于处于大玛丽状态，他可以撞开砖块后继续向上移动，但却不能进入第一条路径。

clause 部件：该部件中玛丽需要从最左侧到达最右侧才算是验证成功，但是注意到右侧有足够多的火墙，这使得玛丽即使以最快的速度移动也无法避开。因而我们需要使用游戏中另的一个元素——无敌星星，部件中的三个问号方块都有无敌星星，如果玛丽吃到星星就可以穿过火墙。因此，只有当这三个问号方块中至少有一个方块被撞开过，玛丽才能在验证时中通过 clause 部件。

现在所有的部件都实现了，而且归约显然可以在多项式时间内完成，所以我们就有以下定理

定理 1：「超级玛丽」属于 NP-hard。

3. PSPACE-hard 框架

接着，我们介绍一个用于证明 2D 游戏属于 PSPACE-hard 的框架，这个框架来自文献 [1] 和 [3]。它使用的归约问题是 TQBF 问题（True Quantifified Boolean Formula），指的是问某个含有「存在」和「任意」符号的逻辑公式是否可满足，比如问公式

的真值是否是 T。

这里我们对原始论文中的框架作了一些修改，希望能够帮助理解。和之前 NP-hard 框架一样，我们需要定义一些部件。NP-hard 框架中讨论的部件我们就不再重复定义了，这里我们主要定义两个部件，open-close door 和 alternation 部件。

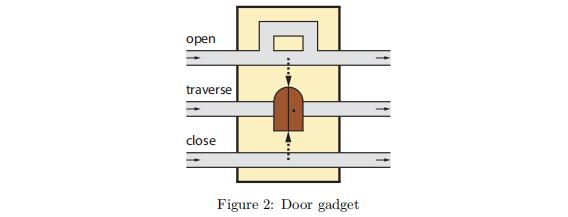
上图是一个 open-close door 部件，它包含三条平行的、不连通的路径，从上到下依次为 open 路径、traverse 路径和 close 路径。traverse 路径上有一扇门，只有当门在打开的状态下，角色才能穿过 traverse 路径；当角色通过 open 路径时，它可以打开这扇门；而当角色通过 close 路径时，它必须关上这扇门。

这个 open-close door 相当于是一个状态存储器，门的开闭相当于 0 和 1，每一个 open-close door 部件保存了 1bit 的信息。这也是为什么加上这个部件后，框架的复杂性可以到达 PSPACE-hard。

接着我们介绍 alternation 部件，它其实是一个辅助部件，用于简化框架的描述。我们可以用其他部件的组合来实现 alternation 部件，不必真的在 2D 游戏中实现它。

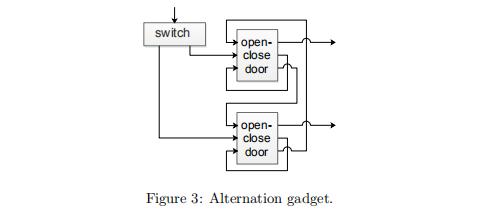
上图是 alternation 部件的结构。该部件中包含两个 open-close door 部件，其中一个 door 处于打开状态，另一个处于关闭状态。不妨假设现在上方的 door 是打开的，下方的 door 是关闭的。角色从左上进入 switch 部件，它只能通过上方的 open-close door 的 traverse 路径，然后再通过 close 路径，这样上方的 door 就被关闭，接着角色通过下方 open-close door 的 open 路径，这样下方的 door 就被打开。可以看到，每次角色通过 alternation 部件后，两个 open-close door 部件的状态就会翻转，这样一来，角色就会从两个出口交替离开。也就是说，当角色第一次进入 alternation 部件时，它会从下方的出口离开，当角色第二次进入时，它会从上方出口离开，以此类推。

现在我们就可以用例子来说明如何构造 PSPACE-hard 框架，对于公式

2D 游戏的框架如下图

角色从 start 部件出发，进入对应变量 x1 的部件，由于限制 x1 的量词是「任意」所以这里是 alternation 部件，因为是第一次进入，角色只能选择从对应 x1 的出口离开，接着角色打开所有对应于 x1 的 open-close door，并关闭所有对应于非 x1 的 open-close door。完成这些后角色来到 merge 部件，之后进入对应变量 x2 的部件，由于限制 x2 的量词是「存在」所以这里是 switch 部件。就这样，角色完成所有变量的一次赋值后进入验证过程，这个验证过程与修改后的 NP-hard 框架是类似的。完成一次验证后，角色进入中间上方的 alternation 部件，注意这时角色是第一次进入该 alternation，所以角色只能从左侧出口离开，接下来角色将再次进入对应于 x3 的 alternation 部件，这时角色只能选择对应于非 x3 的出口，在操作完对应的 open-close door 后又一次进入验证过程，这其实就模拟了「...... 对任意 x3 的赋值公式的值为 T」。所以，当公式中有 n 个「任意」量词时，框架中的验证过程可能会被通过 2^n 次，只有当角色完成了所有的验证过程后，才能最终到达 finish 部件。

容易验证，这个框架模拟了 TQBF 问题。因此，如果 2D 游戏中能实现 start、finish、turn、switch、merge、one-way、crossover、open-close door 这些部件，那么这个 2D 游戏就属于 PSPACE-hard。

另外有一点需要提一下，NP-hard 框架中的部件的每条路径只会被角色通过一次，而 PSPACE-hard 框架中的路径就可能会被通过很多次了，这在构造部件时是需要注意的。

4. 超级玛丽属于 PSPACE-complete

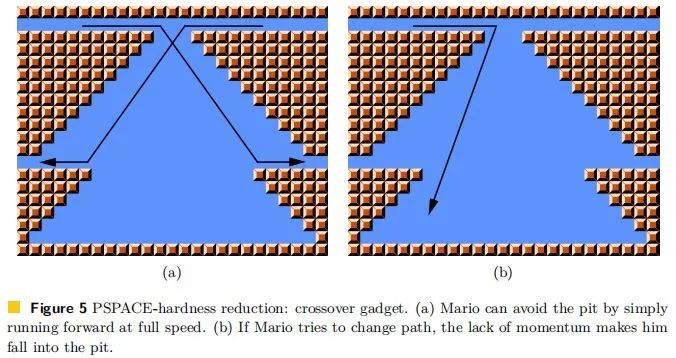
为了证明「超级玛丽」属于 PSPACE-hard，我们需要在游戏中实现 start、finish、turn、switch、merge、one-way、crossover、open-close door 部件，其中很多部件是非常简单的，就不提了，这里就介绍一下 crossover 和 open-close door。

注意，这里与 NP-hard 证明中不同的是，玛丽总是处于小玛丽状态的。

上图就是 crossover 部件，玛丽需要以最快的速度移动才能从左上到达右下（或从右上到达左下）。容易发现，这两条路径不会互相干扰，而且玛丽可以无限次地通过这个部件。

上图是一个 open-close door 部件。open、traverse 和 close 三条路径在图上已经标出来了。该部件中刺猬怪物的所在位置表示门的开闭，上图中门处于打开状态。当玛丽从 close 路径进入时，由于刺猬的存在玛丽无法通过，所以它必须到达砖块下方，等刺猬移动到砖块上方时，在合适的时机撞击砖块，使得刺猬跳过一个方块到达左侧，而后才能通过 close 状态。注意这时门就处于关闭状态了，因为玛丽无法通过 traverse 路径。下面的图展示了具体的过程

现在，我们已经基本证明了超级玛丽属于 PSPACE-hard。而又因为「超级玛丽」游戏的所有状态都能够存储在多项式空间内，所以「超级玛丽」属于 NPSPACE。再根据 Savitch's Theorem，NPSPACE=PSPACE，「超级玛丽」就属于 PSPACE-complete 了。

5. 完善归约

在给出最后的定理前，归约中的两个小 bug 可能需要再讨论一下。

一个 bug 是 open-close door 部件中央的火球。在「超级玛丽」原始游戏中，似乎没有像这样将火墙（球）放置在空格中的例子。不过这个问题比较好解决，只要把中央的火球替换成下面这样的一大排火墙就行了。这样一来，刺猬的移动不受影响，但是玛丽无法通过这些火墙。

另一个 bug 是关于刺猬怪物的生成。在归约中我们需要将刺猬放置在指定的位置，但在「超级玛丽」原始游戏中，一个在天空中移动的怪物会有规律地抛出怪物蛋，当蛋落地后才形成刺猬。当然，这个问题的解决方法也已经在论文中给出了。我们可以将所有 open-close door 放到整个地图的上部排成一行，当游戏开始时玛丽在这些 door 的上方移动，空中的怪物有规律地抛出刺猬，这些刺猬将通过一些漏斗进入各个 door 部件。我们可以设置合适的距离，使得即使玛丽以最快的速度移动，每个 door 都会有一个刺猬进入。完成这些之后，玛丽可以踩死空中的怪物，然后就进入上面框架中提到的 start 部件。

处理掉这两个小 bug 后，我们终于能放心地得到下面的定理了

定理 2：「超级玛丽」属于 PSPACE-complete。

6. 总结

我们介绍了两个用于证明 2D 游戏计算复杂性的框架，并详细解释了如何用这两个框架讨论「超级玛丽」的计算复杂性。「超级玛丽」最终被证明是属于 PSPACE-complete。事实上，文献 [2] 还讨论了一些含有其他元素（比如使用管道移动、获得金币奖励生命）的「超级玛丽」游戏的复杂性。

如果要评选最有趣的关于电子游戏计算复杂性的论文，我相信「超级玛丽」这个肯定能上榜。最后附一下论文的截图

参考资料：

[1] Greg Aloupis, Erik D Demaine, Alan Guo, and Giovanni Viglietta. Classic Nintendo games are (computationally) hard. Theoretical Computer Science, 586:135–160, 2015. arXiv 链接

[2] Erik D. Demaine , Giovanni Viglietta, and Aaron Williams. Super Mario Bros. Is Harder/Easier than We Thought. 8th International Conference on Fun with Algorithms (FUN 2016).

[3] Giovanni Viglietta. Gaming is a hard job, but someone has to do it! Theory of Computing Systems, 54(4):595–621, 2014. arXiv 链接