蜂窝猜想另有巧妙证明！

4世纪古希腊数学家佩波斯提出，蜂窝的优美形状，是自然界最有效劳动的代表。他猜想，人们所见到的、截面呈六边形的蜂窝，是蜜蜂采用最少量的蜂蜡建造成的。他的这一猜想称为“蜂窝猜想”，这一猜想跨越了1600多年才让世人看到了能解决的曙光。

01.美国人黑尔的证明文章搜不到，我们就自己寻找解决方案 

2006年加拿大科学记者德夫林在《环球邮报》上写道，历经千年探索，数学家终于证明了蜜蜂是世界上最高效的建设者。数学家们都认可了黑尔的证明，我们当然也相信。只是一直找不到相关的完整论文，通过百度谷歌也搜不到。于是我们就尝试思考是不是还有别的方法也可证明蜂窝猜想。

结果还真找到了新的思路。蜂窝大家都见过，每个蜂蜡隔墙的厚度和误差都很小。六面隔墙的宽度完全相同，墙与墙之间的角度正好是120度，形成一个完美的几何图形。人们一直在问为什么蜜蜂不让它们的巢呈现三角形、正方形或其他形状？为什么隔墙是平的而不是弯曲的？为什么六块隔墙是一样的，而不是选择长边就柱子高些，短边就柱子短些？虽然蜂巢是一个三维建筑，但每个蜂巢是正六边形柱体，而蜂蜡墙的总面积只与蜂巢的横截面有关。这就引出了一个数学问题，即寻找面积最大周长最小的平面图形。

1943年，匈牙利数学家陶斯巧妙地证明了在所有首尾相连的正多边形中，正多边形的周长是最小的（含曲线）。当正多边形周长为正六边形时一定会比其他任何形状都要小，陶斯无法证明这一点。但美国数学家黑尔证明了平面比凹凸面更省材，但为何选六边形而不是八边五边则没看到有相关叙述。他把19页的证明过程放到了网上，许多专家都看过证明，并相信黑尔的证明是正确的。可惜我们搜不到，正如哈肯完成的四色猜想证明一样，我们也搜不到。但这激发了我们自己去寻找答案。 

02.费马螺线模型与n维空间的最少相邻点公式 

证明这个数学命题跟空间最优化区分有关，尤其是一维空间的最优化区分数到底是多少，此秘密必须打探清楚，这就追溯到了有关素数分布的数论核心中，因此哥德巴赫猜想被证明，其意义重大。认为哥德巴赫猜想不像黎曼猜想那样能广泛地同很多数学领域发生关联，是个误解，很多大数学家也低估了哥德巴赫猜想，高估了黎曼假设，认为哥德巴赫猜想仅是个孤立问题。由此更可见朗兰兹纲领的核心精神可贵，它断言所有的问题几乎都可以跨界解决，数学中没有真正的孤岛。但在尚未贯通之前，则需要遵守“领域互不重叠原则”，不重叠并不代表彼此孤立。

哥德巴赫猜想的本质是相邻论，它是最优化问题。区分n维空间的内部结构必须具备的最少相邻格点数，可由相邻论函数公式 f（n）=2^n 找到。相邻论打探到了整数间离散量的相邻延伸同连续量的相邻延伸有着神秘的关联（以最密集的离散量自然数为枢纽）。通过相邻极限运算可将“部分超越数"回归到代数数中。

相邻论带来了数学新发展，区分一个目标的最优化选择，衍生出了密码学、勘探学和预测学问题，这是数论所带来的应用。更深层次的应用是，它可对大自然和心灵世界进行探秘，用迭代无漏相邻运算推知任意生命和个体的未来和过去以及内外相邻存在，因为所有的自然语言都可以用符号语言取代，数学应用于心理学并不突兀。哥德巴赫猜想的不孤立性还表现在，序数1具有决定意义，很多信息孤岛在此发生关联。这也就是为什么随着哥德巴赫猜想证明的完成，许多数学问题如蜂巢猜想及六度分隔理论会像多米诺骨牌一样被攻克。正如四色猜想，就是哥德巴赫猜想两素数原理成立的一个推论，六度分隔理论也是哥德巴赫猜想的一个推论。根据相邻论函数公式 f（n）=2^n，一维空间的最优化区分种的元素种类数为2类，即哥德巴赫猜想“1+1”。二维空间是一维空间的2次方，显然二维平面的最优化区分元素为 2×2=4类，故任意给定地图，四色区分足够。

同样，六度分隔理论所描述的对象不是发生在平面中，而是发生在三维空间中，因此根据相邻论函数公式 f（n）=2^n，即三维空间的最优化区分元素为 2×2×2=8 类，故任意给定空间（陌生人 A、B 之间的关系），8 类区分足够。8 减去 A、B 两个陌生人，那么中间分隔的就是 6 个人。如果不理解哥德巴赫猜想的本质，就难以知道用该方法证明六度分隔理论，原来素数可以成为网格中的每一个格点单元序。串联代表费马双螺线的弧长延伸，并联代表费马双螺线的极径延伸，三维网格的并联区分，两类色块链足够。 

03.哥猜获证显示了一维空间的最优化区分数是2，一维空间只能用素数区分。 

两类并联数与两类串联数的乘积就是区分全部平面网格色块种类数是4，再进行两类叠加就得到空间网格中的 8 数。下面将进行详细证明。这是由费马螺线改造成的费马螺线格网模型。作为一维空间的螺线，两类元素区分足够；作为一维空间的极径，两类元素区分足够。

两类元素足够区分一维空间，这是哥德巴赫猜想两素数原理，一次方的素数连接是一维空间数，一维空间数能产生全部自然数集合，两个互异素数相加能产生大于6的全部偶数，三个互异素数相加能产生大于11的全部全奇数，其本质还是两个素数相加，因为其中一个素数可规定为常量3，可见一维空间上的所有自然数可由两素数确定，而高维空间上的自然数都重叠在一维空间上，即p+q=2n。该原理已被笔者用重合法和相邻论所证明。

一维空间数的任意分布，最少两类素数区分足够。n 维空间数的任意分布，最少 2^n 类素数区分足够。故偶数域可以表达任意格点问题，假如每个格点都是两个相邻点的连线距离的话。

一维网格的串联区分，两类色块足够；二维网格的并联区分，两类色块链足够。即（a+b）（p+q）=2n。这是四色猜想。两类并联数与两类串联数的乘积就是区分全部平面网格色块种类数是4项，4类色彩也就是区分任意地图上所有国家的最少色块种类数。以上就是区分地图，四色足够的证明核心。

一维网格的串联区分，两类色块足够；二维网格的并联区分，两类色块链足够；三维网格的聚联，两类色体足够。即（m+n）（a+b）（p+q）=2n。这是蜂窝猜想和六度空间理论。最少区分元素是8类。

最优化可相邻区分的格点数公式 f（n）=2^n，蜂巢猜想也是如此。4 世纪古希腊数学家佩波斯（Pepos）提出，蜂巢的优美形状是自然界最有效的劳动的代表。他猜想，人们所见到的、截面呈六边形的蜂巢，是蜜蜂采用最少量的蜂蜡建造成的。他的这一猜想被称为“蜂巢猜想”，但这一猜想一直没有人能真正完美证明。黑尔的证明仅完成了平面比凹凸面更省材，陶斯仅完成了正多边形周长更短，为什么选择6这个数，一直没有令人信服的报道。

04.高维空间最优化区分数公式证明了蜂窝猜想，它是哥猜获证的推论。

人们没有想到哥猜获证有广泛的应用，它推导出了多维空间优化区分数公式。用多维空间最少区分数公式就很容易证明。首先区分三维空间的最少元素数目是8，用于空间分隔的最少元素材料类型数是8，蜂巢正是如此，每个蜂巢由天地两个隔板（顶板和底板）和中间六个隔板构造而成。地板可以借势，是省材的；天顶作为开门，不需要材料；如果六个中间隔板是最省材的，就是建筑师的最佳选择。显然连续相连的空间可以借隔板分隔空间，一定是省材的，那么 6 个隔板围成的周长就一定是最小的，即六正多边形的周长相连一定是最小的，而面积是最大的。与边数多相比，圆周相连的小；与边数少相比，等三边形的小；与凹面和曲面相比，平面蜂巢猜想及六度分隔理论的最小，即六正多边形边线内曲和外曲都不及直线相连的正多边形周长更短。因为正六边形连接起来看，直线连接的最短。

而至少需要8个性质互异的元素完成一个隔离空间，不同方向的隔板就是性质互异的元素，这是三维空间的最优化区分数。蜂巢的每个间隔正是 8个元素完成单元隔离的。不同方向的隔板属于不同的元素，向下的 1 块天顶，向上的 1 块地板，垂直于天顶和底板之间的6块隔板，自然就围成3组两两相向的六边形，构成了8大元素。天顶和底板被隔成了正六边形，6块隔板都分别是正四边形。为什么等边最短？因为当6边都等于最短边时，显然正六边形周长是最短的。可见证明蜂巢猜想，其关键是选择6数的最优化理由，是完成隔离的最优化材料种类数，等边和直线的最优化选择理由很容易解决。因此证明蜂巢猜想的核心就是理解三维空间的最优化区分数的来由。在“多维空间最优化区分数公式”这一引理的帮助下证明了以下两点而使蜂窝猜想获证。

1）.取6不取非6。为何优先看重空间最优化区分数？因为区分数的大小直接决定了是否省材。因为单位底面积不变时选择的隔板种类数越多，越耗材。但区分数太少又完成不了可无限延伸的空间隔离，实现不了建筑功能，故存在一个最优化数。这个最优化数就是6，它是可无限延伸的可区分数。其他正多边形未必可无限同类延伸，比如5、4、3数正多边形，其中5就没法延伸出等角的正多边形，4虽可延伸出等角的正多边形但，但3个4正多边形可置换为2个6正多边形，可看出在相同面积中没有正6多边形省材，3也可延伸出等角的正多边形，但6个正三角可合并为一个正6边形，显然在相同面积中也没有正6边形省材。

2）.取直不取曲，取正不取斜。凹凸的面的相邻互补空间与平面的相邻互补空间在获取空间大小上是等价的，但凹凸互补的隔墙与平面互补的隔墙是不一样的，后者直线连接省材。为什么边长是直线而不是曲线？因为两点间的距离，直线最短，尤其是正多边形相连起来看。非正多边形的相邻互补空间与正多边形的相邻互补空间在获取空间量上也是等价的，但斜多边形互补的隔墙与正多边形互补的隔墙是不一样的，后者直线连接比折线连接省材。

无须证明第二条，仅凭完成第一条的证明就能使蜂窝猜想成立。这个证明技巧是独特的，显示了哥猜获证对未解决问题有多米诺骨牌般的推动效应。希望数学界同行，把这一规律敏锐地用起来。 

05.多维空间最优化区分数公式还有更广泛的应用，比如证明六度空间理论。 

多维空间的最优化区分数公式，在哥德巴赫猜想以及四色猜想的证明中已经完成。简洁叙述如下。

定理 1：一维空间连续格网数的任意分布，最少用两个不同素数区分足够。

证明：任意给定的一维空间上的正整数，等价于一维空间连续格网数的任意分布，因此该定理可等价变换为，任意正整数（偶数）可用两个不同素数之和表示，奇数可以用偶数 + 一个常数替代，这个常数可以用最小的奇素数 3 确定，因此区分偶数就区分了所有正整数。于是可知，求证一维空间最优化区分数是2的命题，就等价于哥德巴赫猜想的证明。这个命题，作者在《数学底层引擎相邻论和重合法》一书的首篇论文已经完成证明，本文不铺开讲，澎湃号里已有多篇文章论述过。

二项式奇素数变量可表不小于8的任意偶数。二项式奇素数变量再外加一常数项可表不小于11的任意奇数。合起来，不小于 8 的任意正整数都可以用两类变化着的素数区分。有了哥德巴赫猜想的获证，推导多维空间最优化区分数公式就顺理成章了。这中间使用了一个重要过渡，那就是费马螺线改造成的费马螺线格网模型，此模型描述了一维空间数与多维空间数的等价关系，一维空间数可以等价表示为二维空间数，还可以等价表示为三维空间数，乃至可以等价表示为n维空间数，甚至可以表示n^k维空间数。正整数可以同超越数中的核心变化数一一映射，甚至可以一一等值映射。

线条的对折螺旋可以产生平面；平面再对折螺旋可产生空间；三维空间再对折螺旋可产生四维空间；……，n维空间再对折螺旋可产生n+1维空间。故素数的一维空间数连接可产生n维空间数。于是高维空间优化区分数公式就产生了，即f（n）=2^n。四维空间的最优化区分数公式是16，我们发现很多生物周期跟14、15、16有关，故空间区分是8卦，后天时间的区分是16天，月圆到月暗，月暗到月圆的周期就不超过16天。阴阳两类数是先天时间区分数，16天是后天时间区分数。故时间的最小单位隔离数在16天内，起点和终点两天去除后就是间隔的14天生物周期。可见维度的升级就是线性区分数的升级。蜂巢猜想是根据三维空间的最少相邻点数 2^3 获证的。

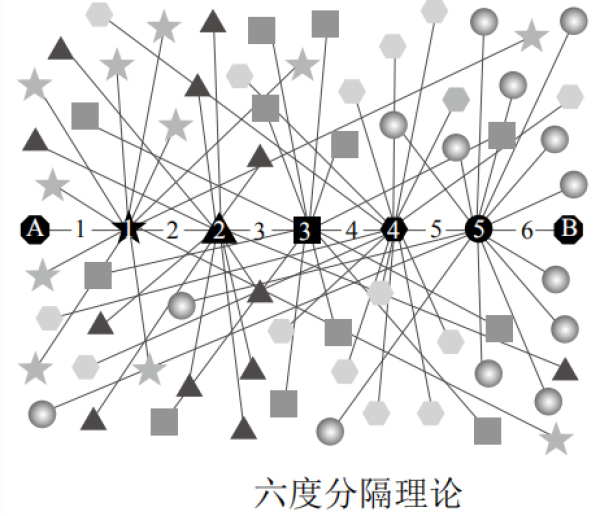
定理 ：任意给定建筑面材大小的蜂巢，选用底面正六边形柱体做单位间隔，可获得最大居住空间。（同理可证）

证明：根据定理 2，任意维度空间的最优化可相邻区分的格点数公式：f（n）=2^n，将三维空间中的 3 数代入公式，可得 f（n）=2^3=8。因此，8是三维空间中的最少可区分元素的数目。8 类区分元素成功分隔

了任意给定空间，因此元素区分数8是获得给定空间的最小数，换句话表达就是，任意给定建筑面材大小的蜂巢，选用底面正六边形柱体做单位隔间，可获得最大居住空间。地板和天窗是不用材料的，因此还剩下 6 个隔板元素进行比拼。6 就成了蜂巢猜想及六度分隔理论的最优化量，而六边形的周长，显然正六边形是最短的，而两点之间的连线又是直线最短，而不是曲线。综合以上所证，任意给定建筑面材大小的蜂巢，选用底面正六边形柱体做单位隔间，可获得最大居住空间的蜂巢猜想判定就得到了证明。

而六度分隔理论也可用以上一样的方法证明。乍一看六度分隔理论似乎是应用问题：如何用最简洁的路径让两个陌生人认识。但这个应用问题跟数论密切相关。由于解决它需要高度抽象的数学形式，于是该问题也就成了纯粹数论问题。六度分隔理论（Six Degrees of Separation）又称小世界效应，它是这样描

述的：假设世界上所有互不相识的人只需要很少中间人就能建立起联系。后来 1967 年哈佛大学的心理学教授斯坦利 • 米 尔 格 拉 姆（Stanley Milgram）根据这概念做过一次连锁性实验，尝试证明平均只需要6个中间人就可以联系任何两个互不相识的美国人，陌生人AB之间隔着 6 条线段，5个隔点。

这种现象并不是说任何人与人之间的联系都必须要通过 6个层次，是表达了这样一个重要的概念：任何两位素不相识的人之间，通过一定的联系方式，总能够产生必然联系或关系。显然，随着联系方式和联系能力的不同，实现个人期望的机遇将产生明显的区别。

怎么理解六度分隔理论，才可判断命题真假？你和任何一个陌生人之间的最少间隔人数不会超过六个，也就是说，最多通过六个人你就能够认识任何一个陌生人。这里的相识关系不是指熟悉的朋友圈，而是指有相同关系，这里的陌生关系，是指相异关系。

每次在与自己有共性的抽象的熟人圈里选择与自己无共性的陌生人连接，不超过选择 6 次，就能连接上任何一个陌生人。如果仅限于在具体的熟人圈里选择，六度分隔理论是不成立的。很容易找到反例。

证明：根据定理 2，任意维度空间的最优化可相邻区分的格点数公式：f（n）=2^n，将三维空间中的 3 数代入公式，可得 f（n）=2^3=8。

因此，8是三维空间中的最少可区分元素的数目。8类区分元素成功分隔了任意给定空间，有人用熟人个数的 6 次方来证明，理由是这个数字很大，足可认识到任意陌生人，显然说不过去。因为不管怎么说，再多这也都是个有限数，通过有限个熟人，让任意空间中的两个陌生生命取得联系，逻辑上没有找到能结识到任意陌生人的允许条件。六度分隔理论，显然又是一个反直觉的判定，有限个熟人通过 6道有限个环节何以能结识到任意陌生人呢？

我们可将认识定义为空间上可相互区分的元素，因此可囊括任意空间远，任意多生命，用天文望远镜可识别对方，就叫认识，理论上这个望远镜是可以接受超光速来取得相互联系的。我们把已认识的关系定义为线条内相邻，假如1类是我直接认识的人，那么2类就是我间接认识的人，3类就是我间接再间接认识的人，如此这般，再经过 4 类、5 类、6 类，就可以结识空间中的任意陌生人了。因此能否结识到任意陌生人，跟已知认识到的熟人有多少数量无关，而跟结识人的方向有关，跟中间人的类型性质有关。

8 类元素是分隔任意给定空间的最小的足够数。A、B 作为 2 个陌生人，再加上 6个中间人，正好是8类元素。A到1类是熟悉关系，也称为直接相邻关系，这种相邻是线条相邻，是一维空间的相邻，由端点到线条；A到1类、2类，我们定义为行走路上的熟人关系，由线条到平面；A到3类、4类，我们定义为充军边疆的国人关系，由平面到空间；A到5类、6类，我们定义为可远到天涯的天人关系，每一类隔板由不同方向来区分，即向量元素，8个不同的向量元素所围成的空间就是任意两个陌生人之间的联络空间。于是定理得证。即任意给定空间中的 A、B 两个陌生人，仅需不超过6个中间人就可取得联系的判定是成立的。(文/罗莫)