数学课｜如何做出最优选择？华罗庚教你一招

原创：吴昊

        

作者 | 吴昊 & 编辑 | 罗数君

文 1691字 阅读时间约 5分钟

导语：

有人说抛开考试，数学对人们的工作与生活作用很小。其实，数学于很多方面都能为人们提供更加严谨、高效的思路。今天我们就以华罗庚优选法为例，探讨它如何帮助人们做出“最优选择”。

提起华罗庚，家长们的第一印象大都是他引领的国内奥数风潮：从苏联访问归来之后，华罗庚受启发于苏联通过大力普及推广数学竞赛来提高人民数学水平并从而加速国家工业发展的实践，他也开始在国内举办大型的数学竞赛，开始了“全民奥数”运动。但当年他之所以家喻户晓，还是主要因为他在全国巡讲统筹法与优选法“双法“，以期帮助各行业的工人最迅捷有效地完成他们的工作。

统筹法大家可能都有所了解，就是通过安排任务顺序和时间，来缩短一串任务的总完成时间。比如课本里的“烧茶水”问题，或是小学奥数里经典的“烙馅饼”问题：如果烙熟馅饼的一面要 1 分钟，那烙熟两面就总共需要 2 分钟。现在有两个炉子，请问最快需要几分钟，能把三张饼烤熟？但提到优选法，很多人可能就一头雾水了。

图片来源：维基百科-华罗庚

其实，统筹法和优选法都属于运筹学（Operations Research）的范畴。运筹学就是通过建模寻找复杂问题的近似最优解，统筹负责安排工序，而优选负责寻找参数。比如假设加工一种零件需要高温（300度 – 400度），但问题在于大家不知道具体多高的温度能最大化加工效率——高一点的温度需要更多时间冷却，而低一点的温度需要更长的加热时间。如何找到一个平衡点呢？

如果实验材料充足且时间充裕，那么对温度进行枚举是个不错的选择。但在现实中，当时环境只允许少量的实验和短暂的时间，这时我们就不能随意选择温度，而要保证在数据点较少的情况下，无论最值在哪里，我们估计的近似值都足够精确。这种选择“好”的数据点来进行近似的方法，就是优选法。

华罗庚在他当时传阅甚广的著作《优选法平台及其补充》的第一章中，便详细介绍了用黄金比例分割取值区间来选择数据点的方法，如图（图并非书中原图）：

图片来源：https://en.wikipedia.org/wiki/Golden-section_search

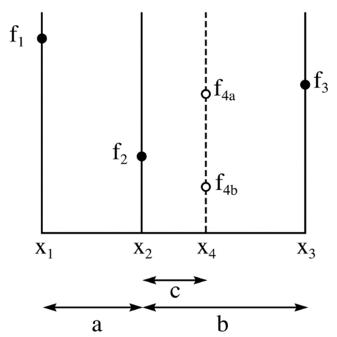
继续上面的例子，我们希望最小化 f 的值，也就是时间。为了简化步骤，我们假设f只有一个极小值（就是两边的值都比自身大的地方），而且 f 相对平滑。X 轴代表温度，纵向轴则代表时间。为了测量边界情况，我们先把 300 和 400 分别代入 x1 和 x3，分别算出 f1 和 f3，并取中间的某一点作为 x2，算出 f2。假设在这个例子中，f2 比边界的两个值都要小，那么我们的探索就还没有结束，所以需要在 x2 和 x3 之间继续寻找 x4 并算出对应的 f4。

如果 f4 在 a 位置，也就是高于 f2，我们的下一步就应该考虑 x1 到 x4 这个区间，因为在 x4 到 x3 这个区间函数突然大跌到最低点的可能性不大；同理，如果 f4 在 b 位置，也就是低于 f2，我们的下一步就应该考虑 x2 到 x3 这个区间。不论哪种情况，我们都要根据现有数据点的排布来估计整体函数的趋势，因为函数在某个区间相对平滑的可能性远大于它突然猛烈下跌、再猛烈上涨的可能性。

那么这和黄金比例有什么关系呢？华罗庚推荐的这种优选法有两个核心理念：第一，不论上一步的结果如何，下一步要测试的取值区间长度都应该相等；第二，每一步前后的取值区间长度比例也应该相等。根据这两个理念，我们得到以下两个式子：

把第一行式子代入到第二行，就可以得到 b/ ( a + b) = a / b 。简单的交叉相乘就可以得到 b^2 =a^2 + ab。如果把 b 设为 1，就能得到 a^2 + a - 1 = 0 求解可得 a = (-1 +√5) / 2 或 (-1 -√5) / 2。后面的这个解明显是负数，所以我们只能取前面的这个解，大约是 0.618，而 a∶ b ≈ 0.618∶ 1 也就是我们常说的黄金分割比。

如果现有材料只够我们做 5 次试验，我们就只需重复上述步骤 5 次，采集到所有数据点中的最小值就是我们所取的近似最小值。是不是很简单呢？

当然，现实中大部分函数都不会只有一个极值，而且也不会像我们这里假设的那样非常平滑。要想在这些复杂的情况中找到最优解的近似值，我们需要更复杂的计算和更多的步骤，但最终优选法的思路还是不变的：通过在现有区间的中间找数据点来不断缩小可能的取值区间，一直到足够精确（看不出上次和本次区别）或者次数已满，这时所采集的所有数据点中的最小值就是我们近似出的最优解。

图片来源：pixabay

这个方法在我们日常生活中当然也可以使用，比如空调设置的温度：如果温度太低会使用大量的电，产生多余的电费；如果温度不够低，则仍需通过其他方式比如买冰镇汽水来降暑。以周为单位做实验的话，可以先设置一个合理区间，比如 16 到 24 摄氏度，然后每周根据上述步骤来采集新的数据点，在暑假过半时取所有点中花费最少钱的温度，来近似最优解。

喜欢这篇文章吗？欢迎给我们留言，探讨有趣的数学问题，如果你还想看其他的相关内容，也可以向我们提出来哦！

阅读原文（“罗博深数学”公众号：LuoboshenMath）