选择困难怎么办：为什么选择最佳配偶的概率是37%？

作者|吴昊&编辑|罗数君

文2566字 阅读时间约6分钟

导语：

数学，是一项十分奇妙的思维活动。从曾经苏格拉底的苹果林到现在秘书申请人的最佳匹配，甚至选择最佳配偶的概率......数学将这些毫无关联的活动用“37%”这个简单的数字紧紧联系在了一起。想知道为什么是“37%”吗？请读者们浏览今天的文章寻找答案吧！

曾经有这样一个故事。苏格拉底带着他的一群学生去苹果林，要求在每个人穿过苹果林时挑选一只自己认为最大的苹果，但是学生们不能回头，也不能选择多个苹果。在终点集合时，学生们纷纷表示对自己的选择不满意。有的抱怨放弃了之前的大苹果，有的抱怨选择得太早，错过了后面的大苹果。然而，苏格拉底语重心长地总结到：“这就是人生——一次无法重复的选择“。但是，作为一名老师，苏格拉底也许应该引导学生们，该怎么选择？

图片来源：pixabay.com/zh/illustrations/

与”如何拿到最大的苹果？“类似的问题还有很多，最著名的就是“秘书问题”。如果有n个申请者同时申请一个秘书职位，你作为人事经理只能选择一个录取，并且不能吃回头草，也就是说，在对每一个秘书候选人面试结束后，你只有两个选择：录用此人，所有面试结束；请其回家，老死不相往来。在这种情况下，你应该用什么样的录取策略，才能最大化被录取者在所有申请者里面最优秀的概率呢？

图片来源：flickr.com/photos/thedailyenglishshow/

这类“最优停止问题”（Optimal Stopping Problem）”看起来很难，不像有什么简单的答案。但是，数学家们偏偏通过计算给出了一个数：1/e，近似于37%。

-这个数是什么意思呢？又是怎么样推论出来的呢？-

当n足够大时（比如n=100），最前面的n/e个申请者不管有多好都不录取，也就是说面试的前（100/2.71828）人，即前37人，不录用，仅供参考。在后面的面试中，只要有一个比前面申请者都优秀的，就立即录取。如果一直都没有合适的申请者，就录取最后一个申请者。通过以上策略所得出录取者的最优秀的概率也恰好等于1/e，近似于37%。

直觉上理解，前面的这n/e个申请者的作用在于“试水”，也就是先估测一下申请者整体的质量。在这之后，如果一个申请者比前面的人都优秀，就说明TA有较高概率是所有申请者中最优秀的人。

图片来源：www.flickr.com/photos/thedailyenglishshow/

具体来说，假设我们用前k个人来试水，那么得到最优解的概率应该是

对一个固定的i来说，如果i是最好的申请者，那么TA被选中的概率就等于TA前面的申请者都被拒绝的概率。也就是说，只有当i-1个人里最优秀的人恰好在前k个必须被拒的申请者中时，我们才可能等到第i个人。图片来源：graphicriver.net/writing-graphics/pg-8

我们注意到，n个人中，任一申请者最优秀的概率都是1/n。同理，前i-1个人中，每个人最优秀的概率都是1/(i-1)，那么前k个人中出现了这个最优秀的人的概率就是k/(i-1)。据此，我们可以把之前的最优解概率写为

你可能已经认出来， 也就是第n个调和级数。在n足够大时约等于ln(n+1)，所以概率等于

注释：调和级数（Harmonicseries）是一个发散的无穷级数。调和级数是由调和数列各元素相加所得的和。（来自百度百科）

调和数列：正整数的倒数组成的数列。例如：1+1/2+1/3+......+1/n+......（来自百度百科）

下图是n=100时，这个函数随k的变化：

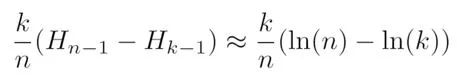
我们可以观察到，这个函数在k为2-100时是个凸函数，所以在其导数为0时就能取得最大值。由此，我们得到导函数

注释：凸函数是指一个定义在某个向量空间的凸子集C（区间）上的实值函数。凸函数还有一个重要的性质：对于凸函数来说哦，局部最小值就是全局最小值。

所以能算出也就是说，在k=n/e时得到的最优选择的概率最大。将k=n/e代入到概率的表达式中，可以得到所以，录取到最优秀申请者的概率约等于1/e，近似于37%。图片来源：giphy.com/gifs/cheer-cheering

虽然这看起来不够完美，但可以证明，这已经是最佳策略了。如果苏格拉底有100个学生，而每个人能遇到大概100个苹果，那么只要他们找到比前37个苹果大的苹果，就可以将它直接收入囊中。按照这个策略，他们中拿到最大的苹果的人数的期望值近似于100x37%=37人，这远远好于没人拿到最大的苹果。

同样有趣的是，有些数学家在选择伴侣时，也采用了这种策略。先找出11个比较适合的约会对象，然后顺序尝试约会，先拒绝掉前4个。从第五个开始，如果找到比前四个都合适的人，就直接结婚。在有些美剧里，约会的双方也会以“You are my 37%”为名打发对方，也是这个缘由。

图片来源：pixabay.com/zh/illustrations/

值得注意的是，这个策略要求读者们提前知道大概有多少个可能的申请者，以此来算出应该先拒绝多少人。类似的，我们可以根据时间来进行筛选。比如，你有一个小时可以在网上购物，假设你浏览每个物品的时间差不多，那么你在前60x37%≈ 22分钟可不要下单哦！但是，如果读者们完全不知道自己的考虑范围的话，那么这个方法就不能用了。

从苏格拉底的苹果，到秘书的选择，再到相亲......这些看起来毫无联系的事情却被37%这个看起来很随机的数字联系到了一起，这就是数学的魅力。它将生活中一个个看起来令人毫无头绪的难题转化为数学推理，从而从另一个角度尝试解决问题，是不是很神奇呢？

喜欢这篇文章吗？欢迎给我们留言，探讨有趣的数学问题，如果你还想看其他的相关内容，也可以向我们提出来哦！

（本文原载于“罗博深数学”：LuoboshenMath）