当1+1+1等于1时——James Propp教授专栏

原创 James Propp zzllrr小乐

本文开场曲——吉格舞曲“爱尔兰浣女” The Irish Washerwoman

（作者在文中举例时有用到）

作者：James Propp教授 2024-12-19

译者：zzllrr小乐（数学科普公众号）2024-12-21

有各种各样的数学运算（操作），其特性是执行两次运算等于什么都不做。这样的运算被称为对合（involution），你可以在数学中随处找到它们：取一个数的负数，取一个数的倒数，将一个物体旋转180度 ⊃1;，否定一个命题，取一个集合的补集，我可以继续举例······。

当执行 X 两次相当于什么都不做时，那么执行 X 三次相当于执行 X 一次，执行 X 四次相当于执行 X 两次，依此类推。在这种情况下，要知道当你多次执行 X 时会发生什么，只需知道你执行 X 的次数n是偶数还是奇数。如果 n 是奇数，则执行 n 次运算与执行一次相同；如果 n 为偶数，则执行 n 次运算与什么都不做相同。（参见我之前的文章“当 1+1 等于 0 时”） 。

试图对所有这种行为方式的数学运算进行分类，甚至只对重要的数学运算进行分类，将是一项艰巨的任务，而我今天的目标不是进行这样的综合调查。但是还有其他一些运算并不完全是对合 – 可以称它们为“准对合” ⊃2; – 它们具有做 3 次等于做 1 次、做 4 次等于做 2 次等性质。这些较罕见的运算是我今天的主题。

对于这类运算，如果你想知道当你做一个运算 n 次时会发生什么，按n 是正奇数、正偶数还是零，对应三种情况 ⊃3; 。与“0、1、0、1、0、1······”的模2算术不同，控制这些运算的计数类型是“0、1、2、1、2、1、2······”。

下面我给你看三个例子。其中前两个是技术性的，但第三个很容易理解，值得被更多地了解。如果前两个看起来太神秘，请随意跳到第三个。

正交补 Orthocomplementation

我们的第一个例子来自线性代数，但为了方便起见，我将切换到三维几何，以通常的方式配备 x、y 和 z 坐标。给定此空间中的一组直线的集合 S，设 Perp(S)或者P(S) 为垂直于 S 中每条直线的所有直线的集合。例如，假设 S 由三条在xy-平面上围出一个三角形的直线组成。然后，P(S) 由平行于 z 轴的所有直线组成，P(P(S)) 由平行于xy-平面的所有直线组成，P(P(P(S))) 由平行于z轴的所有直线组成，依此类推。P(P(S)) 与 S 不同，但 P(P(P(S))) 与 P(S) 相同。

如果我们设 S 是由三条相互垂直的直线组成的集合，就会出现一个更令人费解的例子。那么 P(S) 根本不包含任何直线；也就是说，它是空集，也写成 { }。那么，在这种情况下，我们应该如何看待 P(P(S)) 呢？也就是说，P({ }) 到底是什么？如果你做了很多数学运算，你就可以猜到会发生什么，因为你以前见过我们数学家这样做：我们将“我见过爱尔兰的每一只独角兽”这样的断言视为（空洞的）正确的。（如果你认为我声称见过爱尔兰的所有独角兽的陈述是错的，那就请你找出一只我没见过的；事实上，因为爱尔兰没有独角兽，所以我声称见过爱尔兰所有的独角兽，肯定是一句正确但空洞的话）

因此，对于平面中的每一条直线 L，L 垂直于 { } 的每一条直线（因为 { } 中没有一条直线是不垂直于 L 的，事实上，因为 { } 中根本没有直线），这意味着 P({ }) 是我们空间中所有直线L 的完全集合（全集）。因此我们看到，当 S 由三条相互垂直的直线组成时，P(S) = { } 是不包含任何直线的集合，而P(P(S)) 是包含所有直线的集合，P(P(P(S)))是不包含任何直线的集合，依此类推。同样，P(P(S)) 与 S 不同，但 P(P(P(S)) 与 P(S) 相同。

这并非巧合：可以证明 P(P(P(S)) 与 P(S) 始终相同。

连续执行两次 Perp（取垂直线 perpendicular） 是一种数学家所说的 “闭包” （closure operation）的例子。闭包运算是一种具有这种性质的运算（操作）：一个事物的闭包的闭包与这个事物的闭包相同。也就是说，它是执行 “两次等于一次” 的那种操作 ⁴ 。如果把C(S)定义为 P(P(S))，则 C(C(S)) 为 P(P(P(P(S))))，等于 P(P(S))，即 C(S)；所以 C 是一种闭包操作。

通常，操作 Perp 应用于向量空间（或者更技术上称为内积空间 inner-product space）。你有一些大的向量空间 V 和一些较小的位于 V 内部的向量空间 W 。然后 Perp(W) 是位于V 内部的另一个向量空间，Perp(Perp(W)) 也是如此，依此类推。当 V 是有限维的向量空间时，Perp(Perp(W)) 始终等于 W，但在无限维空间中这不再是正确的。尽管如此，在那些无限维空间中，Perp(Perp(Perp(W))) 始终等于 Perp(W) 仍然是正确的。因此，Perp 是执行“三次等于一次”（thrice-equals-once） 操作的一个示例。Perp(W) 被称为 W 的“正交补”（orthogonal complement，orthocomplement）——因此作为本节的标题。

直觉主义否定 Intuitionistic Negation

我们本文三个“三次等于一次”的运算（操作）案例中最奇怪的是非经典（更具体地说，构造主义）框架中的逻辑否定。在这里，我使用“构造主义的”（constructivist）这个词来表示 20 世纪出现的一种逻辑风格，而不是英文同名的教育运动（建构主义）。构造主义（constructivism）类似于另一个叫做 “直觉主义” （intuitionism）的运动，并且确实与之纠缠不清，事实上，我所说的那种逻辑通常被称为直觉逻辑（intuitionistic logic）。在构造主义的设置中，断言“非p” 的意思更接近于断言“我有一个程序，以给定的 p 的证明作为输入，以 0 = 1 的证明作为输出”（你可以用任何你喜欢的假命题替换 0 = 1）。在经典逻辑中，“p 或 非p” 是一个老生常谈，称为排除中间定律，但这个定律在直觉逻辑中不再有效。事实上，拒绝排除中间的定律（排中律）是数学直觉主义风格的核心。在这种观点下，如果你无法证明 p 是真的，也不能证明非 p 是真的，那么你就没有理由声称知道 “p 或 非p” 是真的。因此，如果一个不果断的哈姆雷特说“明天我要么生存（be），要么毁灭（not be）”，直觉主义者会反驳这个断言，或者至少反驳哈姆雷特声称知道它的理由。

在直觉主义逻辑中，“非非p” 不等同于 p，但尽管如此，p 仍然蕴含着“非非p”，尽管我将用“产生 yield”一词替换“蕴含 imply”一词，以阻止您经典地解释该断言。让我们看看为什么 p 会产生“非非p”。用符号表示，p 的直觉主义否定写为 p ⇒ ⊥，其中 ⊥（将其视为T的颠倒，T表示True真）表示不可能是真的（有时称为“假” falsehood——可能性为假），p ⇒ q 表示“p 的证明产生 q 的证明”。因此，为了证明 p 产生 “非非p”，我们必须证明 p 的证明会产生 (p ⇒ ⊥) ⇒ ⊥ 的证明。在这里，我们可以使用经典逻辑规则的直觉主义版本，称为 modus ponens（假言推理，分离规则），它断言如果 p 为真并且 p ⇒ q 为真，则 q 为真，或者等价地说，如果 p 为真，则 (p ⇒ q) ⇒ q 为真。直觉主义版本说“如果你有一个 p 的证明，那么你有一个程序可以将 p ⇒ q 的每个证明都变成 q 的证明。” 将 q 替换为 ⊥，我们得到我们想要的结果。

由于 p 对所有 p 都产生 “非非p”，我们可以用 “非非p” 替换 p 以获得另一个直觉上有效的断言：“非p” 产生 “非非非p”。我声称相反的含义也成立：即，“非非非p” 产生 “非p”。为了证明它（非正式地），假设我们得到了 “非非非p”。我们必须产生“非p”，也就是说，我们必须产生 p ⇒ ⊥。要做到这一点，只需将 p 视为已知给定条件，看看我们是否可以产生 ⊥。也就是说，我们处于这样一种情况：我们得到了 “非非非p” 和 p，我们想用这些成分产生 ⊥。但在前面一段中，我们证明了 p 产生 “非非p”，因此我们免费得到了第三种成分，“非非p”，我们的目标是使用 “非非非p”、p 和 “非非p” 来产生 ⊥。我们似乎正在偏离轨道，但我们几乎完成了。看看这三种成分中的第一种和第三种，即 “非非非p” 和 “非非p”。前者等价于 “非非p” ⇒ ⊥，因此我们可以将其与 “非非p” 相结合得出⊥。因此，我们已经成功地证明了 “非非非p” ⇒ “非p”，即便如果你的大脑和我一样，你也不太明白这个技巧是如何完成的。

（这个证明让我想起了小说《好兆头》Good Omens的开头，其中三个婴儿被调换得如此频繁，以至于我永远无法理解它！）

无论如何，既然我们已经证明了 “非p” 蕴含着 “非非非p”，反之亦然，我们已经证明了 “非p” 和 “非非非p” 在逻辑上是直觉主义意义的等价物，所以直觉主义否定是“三次等于一次”操作的另一个例子。⁵

网络 Networks

我们的最后一个例子来自组合学，更具体地说是图论，但我会把它表述为人们在社交网络中相互联系的方式。想象一个网络，其中节点对应于人，两个节点之间的链接表明两个链接的人彼此认识。（我将假设如果 A 认识 B ，那么 B 就认识 A 。）然后，对于网络中的任何一组人员的集合S，我们可以将 K(S) 定义为认识 S 中每个人的一组人员的集合。

很容易将 K(S) 与认识 S 中某个人的那群人的集合混淆，所以让我举一个例子来帮助消除混淆。

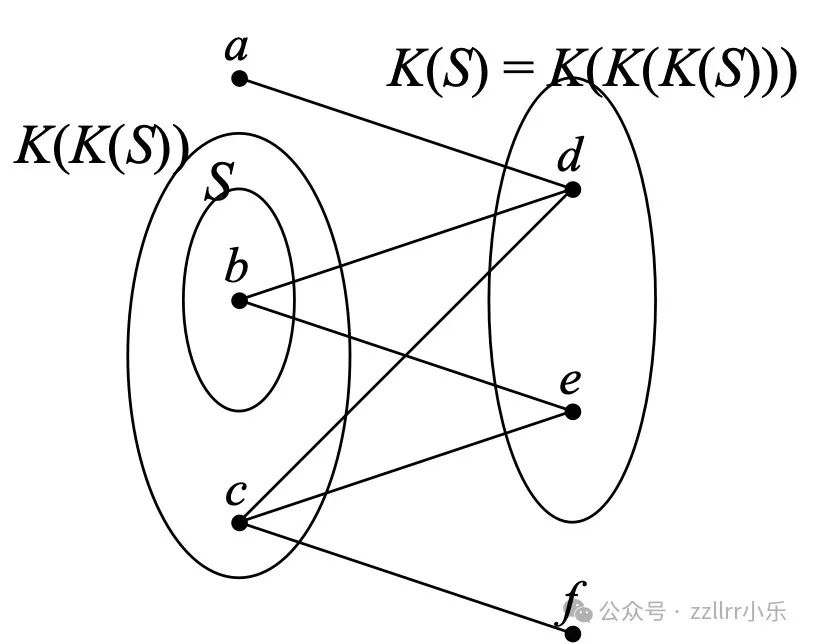
假设我们的网络由六个人 a、b、c、d、e 和 f 组成，如上图所示，当两个相应的人彼此认识时，两个节点通过链接连接起来。设集合 S 为 {b}，其唯一元素为 b 。那么 K(S) 由 b 认识的每个人组成，所以 K(S) 由 d 和 e 组成。现在，在它们两个之间，d 和 e 认识 a、b 和 c，但 b 和 c 是 d 和 e 都认识的，所以它们是 K(K(S)) 中仅含有的元素。也就是说，K(K(S)) 是 {b，c}，而不是 {a，b，c}。那么 K(K(K(S))) 呢？你应该检查它是否为 {d，e} —— 与 K(S) 相同。

我第一次遇到这种 K-运算 时，我还是伯克利的一名数学研究生，当时我正在为我的预考做准备；其中一个练习题要求我们（用图论术语）证明 K(K(K(S))) 等于 K(S)，而不管网络的细节如何。我想这个问题一定是某种“栗子”（尽管它长在一棵相当特殊的“树”上），而且我在职业生涯的后期会遇到它，然而我从来没有遇到过。大约三十年后，我判断这样一个好问题值得广泛的读者关注，如果还没有人写过关于它的文章，那么这个责任就落在了我身上。因此，我发表了一篇名为“社交网络中的伽罗瓦连接”（A Galois Connection in the Social Network，《数学杂志》 Mathematics Magazine 85卷，34-36页 https://faculty.uml.edu/jpropp/galois.pdf ）的文章，描述了这个问题，证明了结果，并将其与一些更高级的数学联系起来。（上图改编自该文章）。

断言 K(K(K(S))) 的每个元素都是 K(S) 的一个元素，反之， K(S) 的每个元素都是 K(K(K(S))) 的一个元素，可以在 S 仅包含一个人的特殊情况下表示为：“认识所有认识所有认识你的人都是你认识的人，而你认识的人都是认识所有认识所有认识你的人。” 按照吉格舞曲“The Irish Washerwoman”的曲调唱出这些词的练习留给喜欢音乐的读者。

相同还是不同？

由于这篇文章是关于 “一等于三 ”的情况，所以第1个例子实际上是伪装的第3个例子，这种说法再合适不过的了。你可以在我的《数学杂志》文章中读到 K(K(S)) = K(S) 的证明，其中并未假设网络是有限的。因此，在第一个例子的几何情况中，想象直线是人，而两条直线恰好在垂直时是朋友。在此上下文中，K 是 Perp，因此 K(K(K(S))) = K(S) 意味着 Perp(Perp(Perp(S))) = Perp(S)。

第二个例子是否与其他两个例子相同？我将让读者在评论部分澄清这一点，因为我已经晚了两天发布这篇博客。

同时，让我承认这篇文章的早期版本包含一个错误。在点集拓扑中，有一个操作（运算）称为取拓扑空间的子集 S 的外部（我们将其写为 Ext(S)），多年来，我一直认为 Ext(Ext(Ext(S))) 始终等于 Ext(S)。但我最终意识到，这种相等性可能会失败。帮助我弄清楚这一点的一件事是 Kuratowski 的闭包补问题的证明百科Proof Wiki文章https://proofwiki.org/wiki/Kuratowski%27s_Closure-Complement_Problem 。这种相等有时会失败，但 Ext(Ext(Ext(Ext(S)))) 等于 Ext(Ext(S)) 始终是正确的。所以 Ext 是我所知道的“1+1+1+1 等于 1+1”（但1+1+1 不等于 1）的唯一例子。

说到网络资源，你可能已经注意到，多年来我经常向我博客的读者推荐相关的维基百科页面。维基媒体基金会（Wikimedia Foundation）在信息生态系统中发挥着至关重要的作用，因此如果您最近没有这样做，请在此时支持它！捐款可以免税，有助于保持互联网健康。

尾注

#1. 在量子物理学中，如果你正在处理那种叫做费米子（fermion）的物体，那么物体绕轴旋转180度不是对合，而旋转360度才是！这个话题值得一写，而且最终会有一篇文章来介绍它，但在那之前，你可以从我过去的文章中学到更多的东西《带锯片、臭虫灭火器、橡皮筋和我》和《汉密尔顿的四元数或三元数的麻烦》（参阅 ）。

#2. 据我所知，最接近描述此类操作的技术术语是“三阶的幂等”。

#3. 在这些设置中，数字 0 的古怪状态让我想起了我的离散数学课程中的许多学生在吸收 0 是偶数这一事实时遇到的困难。我在上课的第一周解释了为什么 0 是偶数，并回到了整个学期如何定义“偶数”和“奇数”的话题，但是，到了考试时，我还是会收到一两个学生的电子邮件，说“我一直忘记，零是偶数还是奇数？在数学上未经训练的大脑中，有一些东西抵制将 0 与 2、4、6、8······分类因为 0 似乎与正偶数整数截然不同。我今天谈论的运算并不能验证学生认为 0 可能很奇怪的倾向，但它们确实验证了学生认为 0 是有所不同的潜在感觉。

#4. 闭包操作（运算）的另一个词是 “二阶的幂等”，通常简称为幂等（idempotent）。

#5. 有关直觉主义三重否定的更多信息，请参阅在Stackexchange网站的讨论。 https://math.stackexchange.com/questions/2453533/triple-negation-in-intuitionistic-logic

参考资料

https://mathenchant.wordpress.com/2024/12/19/when-111-equals-1/

https://faculty.uml.edu/jpropp/galois.pdf

https://proofwiki.org/wiki/Kuratowski%27s_Closure-Complement_Problem

https://math.stackexchange.com/questions/2453533/triple-negation-in-intuitionistic-logic

科普荐书