怎样优雅地画驻波模型图和惠更斯原理图？

以下文章来源于物含妙理 ，作者薛德堡

物含妙理.

境自远尘皆入咏，物含妙理总堪寻。

在讲本文主题之前，诸君先思考一个稍微简单点的问题：若将函数图像的横轴弯曲，例如变成圆，则函数图像将如何变化？

例如，函数

的图像：

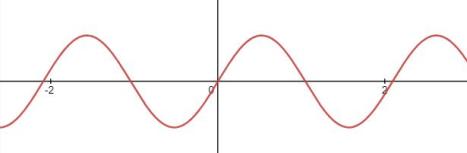
若把它的横轴替换成半径为10的圆，则是下面这个样子。

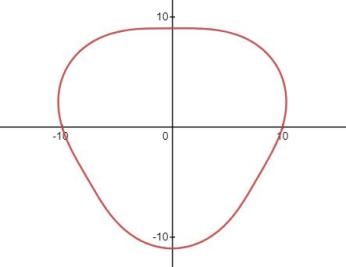
是不是很无聊？为什么要做这种无用的事？

不不不，这件事在物理学中很重要。

1913年，丹麦物理学家玻尔（Niels Bohr，1885-1962）在卢瑟福模型和巴耳末公式的启发下，提出了一种新的氢原子结构模型。

Niels Bohr (1885-1962)

该模型后被称作“波尔模型”，它包含三条假设，即定态假设，频率假设和量子化假设。玻尔模型几乎与所有的实验结果一致，波尔大获成功。

量子化条件即

，其中

为角动量，

为从1开始的整数，

，考虑圆轨道运动，则

故得

，即

1924年，法国物理学家德布罗意（Louis de Broglie，1892-1987）提出的物质波假设，即

其中

是电子的波长，不考虑相对论时

，故得

所以，氢原子的电子轨道的周长是其波长的整数倍，这就是氢原子的驻波模型。

若要把驻波模型的样子给画出来，该怎么画呢？

没错！就按照上述思路，将正弦函数移植到圆上就行了。

假设圆轨道周长是波长的9倍，波的几率幅为1，则在半径为10的圆上画出来是这样的：

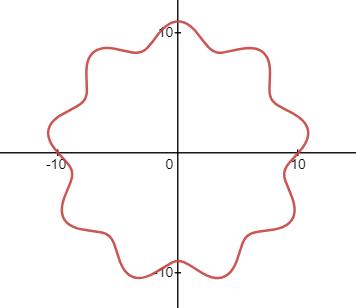
那么，具体是怎么个移植法呢？

很简单，只要在圆的半径上叠加函数值

，作为径向距离就行了。

例如上面这个，叠加后在直角坐标系中的径向距离是

其中

是为了得到

。不过，因为

的定义域的问题，画出来的图有断点。

换成极坐标就可以完美解决问题，径向距离用

表示，即

在网上找一个绘图程序，直接输入上式，就得到上面的图形了。

在此推荐一个很好用的绘图工具，地址为：

https://www.transum.org/Maths/Activity/Graph/Desmos.asp

如果将圆轨道以虚线画出来，加上驻波曲线，得到

时的驻波模型图如下。

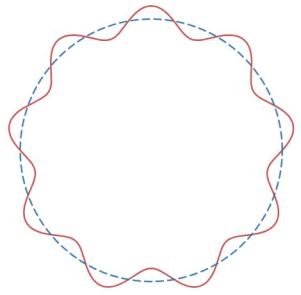
下面到本文的第二个问题——画惠更斯原理图。

Christiaan Huygens (1629-1695)

1678年，荷兰物理学家惠更斯(Christiaan Huygens，1629-1695)为了解释波的传播，提出：

介质中波动传播到的各点都可以看作是发射子波的子波源，而在其后的任意时刻，这些子波的包络面就是新的波前。

此即惠更斯原理。据此原理，平面波在均匀介质中保持为平面波，而球面波也保持为球面波，如下图所示。

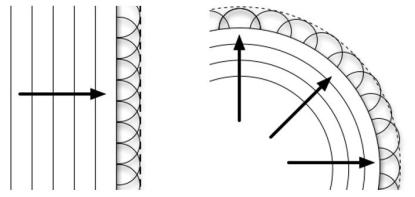
怎样优雅地画出上面这样的图呢？

当然，你可以用任何高级语言编个程序来完成，但总感觉那样太大动干戈了。能否像上面画驻波模型那样简单呢？

当然可以！只要先把半圆排成一列，再像上面那样，移植到一个大圆上就行了。

但问题来了，半圆的方程为

其图像如下：

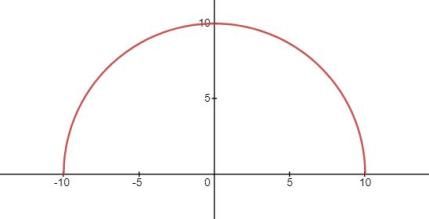
它不是周期函数啊！怎么才能排成一列呢？

有人可能会说，很简单啊，只要这样就行了：

x∈[20n-10,20n+10)。但由于借助了整数

，这个周期函数无法被网上的函数绘图程序识别。

怎样才能借助通用的算符构造一个周期函数呢？

读到这里，在看本人给出的方法之前，诸君可先独立思考一下，说不定你可以有更简单的方法。

本人原创的方法很简单，借助神奇的算符mod，它是用来取余的，例如：

由于它是一个通用的函数符号，就像sin和cos那样，几乎所有的程序都认识它，所以可以放心使用。

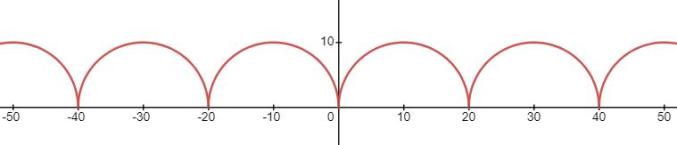
借助它，基于半圆，构造周期函数为：

画出来是下面这样的

若想往左移动一个半径的距离，可改为如下形式：

这样画出来就是

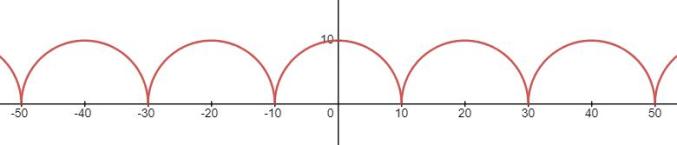
我想诸君应该看出规律了吧！

是的！任何函数，只要用mod函数，把自变量

变成

就得到一个周期为

的函数了！

例如函数

，它的图像为

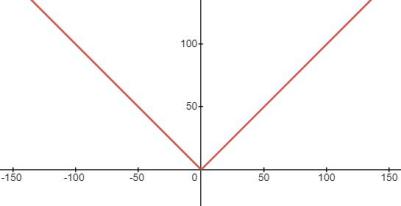
按上述规则，得到周期为20的函数为

其图像为

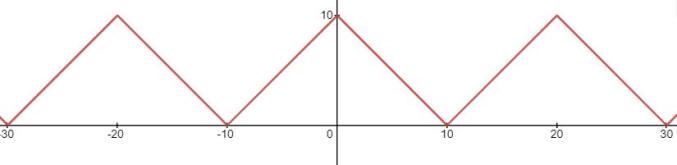
再例如，对抛物线

，对应周期为20的函数为

其图像为

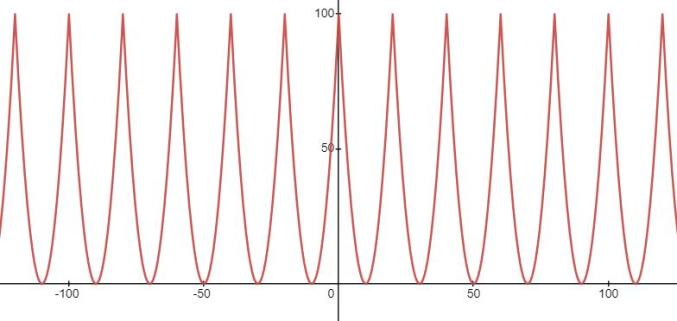
好了，构造周期函数的的问题解决了，现在可以画惠更斯原理图了！

根据上面所讲，有了基于半圆构造的周期函数，只需将它移植到一个波阵面上就行了。

例如半径为

的半圆，构造周期为

函数为

将它移植到半径为100的球面波上，显然，此时自变量

相当于大圆上走过的路径长，即

故得绘图函数为

画出的图为

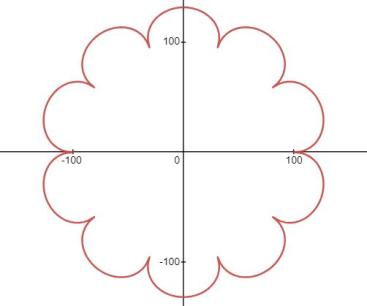
若同时画上内外两个大圆，则得到球面波的惠更斯原理图如下。

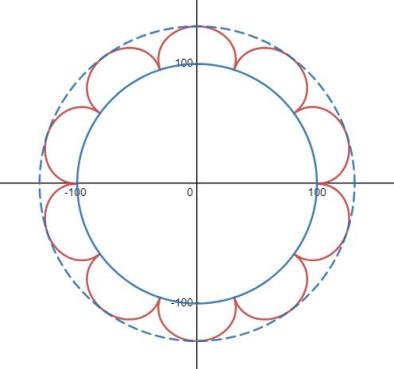
至于平面波，基于半圆的周期函数图就是惠更斯原理图，不再赘述。

作为全文总结，把两个驻波和一组球面波组合，得到一朵奇妙的花——源自物理世界的理性之花。

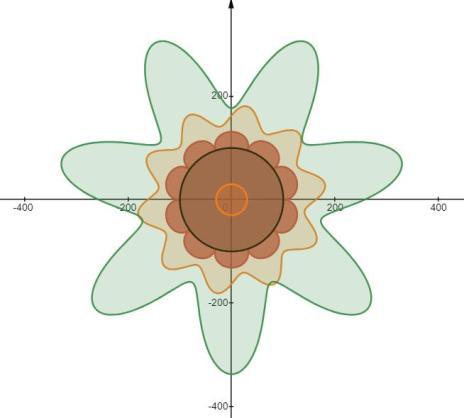
凡是看到这朵美丽之花的人，都会有好运。

在上文《怎样优雅地画驻波模型图和惠更斯原理图？》（以下简称原文）中，通过基于mod函数构造的周期函数，给出了一种绘制惠更斯原理图的简单方法。

原文发布后，自我感觉有两个地方不够完美，故作补充说明。

第一，构造周期函数后，自变量任意偏移后的图像画法，原文没有给出。

例如半圆函数，其周期函数为：

若要向右偏移

，只需要在

后减

即可，即

例如下面是周期函数（红色线），以及分别偏移5，10和15后的3个函数，画在一起的效果图。

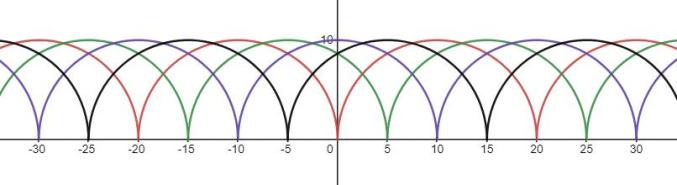
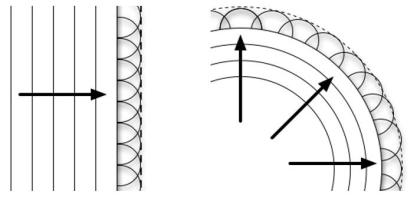
第二，原文中，惠更斯原理图没有采用流行的画法。

具体讲就是小球面波相互交错。相邻小圆不是相切，而是过彼此的圆心，如下图所示。

其实这一点很容易做到，只要再加一个偏移半个周期的图像即可。

例如，对原文中半径为

的半圆，构造周期为

函数为

它偏移半个周期的函数为

它们分别移植到半径为100的球面上后，得到的绘图函数分别为

和

两个图画在一起，效果如下

加上内外两个大圆，就是流行的惠更斯原理图的画法，即

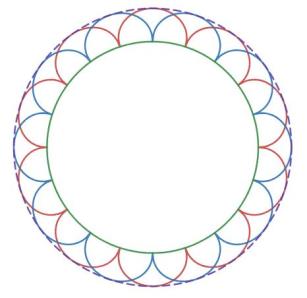
但需要指出的是：这种画法并不是必须的！

有人认为这样画法才能保证包络线是圆，这种理解是不对的！

因为，无论交错的圆多么密集，只要不是无限密，它们的包络线就不可能是完美圆形！

例如，上面的周期函数

的图像，得到的图形如下

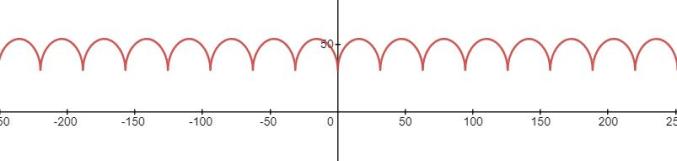
图像并非水平直线！这说明

所以，惠更斯原理图的流行画法中，小圆的包络线不是圆形！

既然如此，交错圆的画法并无必要。

因此，原文中中对惠更斯原理图的如下画法，虽不流行，但并无不妥。

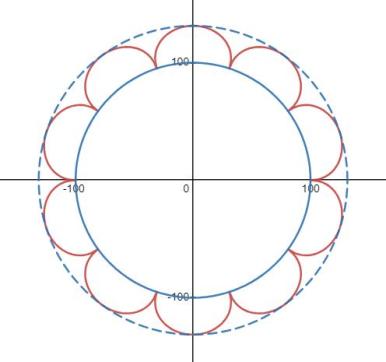
再顺便看看，有没有周期函数，它移植到圆上后，能通过有限的偏移函数相加后得到完美圆形？

第一个例子，方波周期函数，即

它的图像为

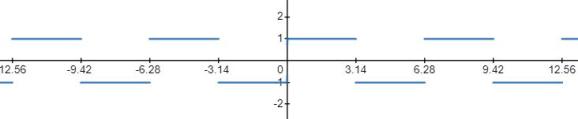
显然

所以，此函数移植到圆上之后，与偏移半个周期的函数叠加后，图像是圆形。

第二个例子， 函数

和

，由于满足

和

当移植到圆上后，它们分别与偏移半个周期的函数叠加后的图像，也是圆形。

除此之外，还有没有什么周期函数，能通过与有限的偏移函数相加得到常数？

留给读者思考。

END

更多精彩文章请点击下面“蓝字”标题查看：

CALL FOR PAPERS｜《物理与工程》征稿量子世纪年乌云里的常数——4.14话h会议纪要｜2024年全国高等学校物理基础课程教育学术研讨会2023版《理工科类大学物理课程教学基本要求》内容细化修订解读中国大学物理教育MOOC联盟2023年工作会议（扩大）暨典型案例交流会 会议纪要2021年《物理与工程》优秀论文、优秀审稿专家、优秀青年学者名单王青教授：源自苏格拉底的问题驱动式教育——在互动中共同学习和成长读后感：教育中的现实和远方王青教授：昨晚（6月9日），清华电动力学期末考试朱邦芬院士：“减负”误区及我国科学教育面临的挑战《物理与工程》2024年第1期目录乐永康：新冠肺炎疫情防控下美国物理实验教学及中美情况对比顾牡：对于重新制定的《非物理类理工学科大学物理课程教学基本要求》的认识和体会朱邦芬院士：从基础科学班到清华学堂物理班朱邦芬院士：对培养一流拔尖创新人才的思考李学潜教授：物理是一种文化李学潜教授：如何帮助物理系学生迈过从高三到大一这个坎穆良柱：物理课程思政教育的核心是科学认知能力培养穆良柱：什么是物理及物理文化？穆良柱：什么是ETA物理认知模型穆良柱：什么是ETA物理教学法吴国祯教授：我的国外研究生经历印象——应清华大学物理系“基科班20年·学堂班10年纪念活动”而写

陈佳洱，赵凯华，王殖东：面向21世纪，急待重建我国的工科物理教育王亚愚教授：清华物理系本科人才培养理念与实践葛惟昆教授：关于中外人才培养的几点思考安宇教授：为什么传统的课堂讲授模式需要改变安宇教授：其实教学就是积累的过程刘玉鑫教授：关于本科生物理基础课程教学和教材编著的一些思考沈乾若：重创理科教育的美加课程改革Henderson C：美国研究基金支持下的物理教育研究及其对高等物理教育的影响《物理与工程》期刊是专注于物理教育教学研究的学术期刊，是中国科技核心期刊，1981年创刊，欢迎踊跃投稿，期刊投审稿采编平台：

http://gkwl.cbpt.cnki.net

欢迎关注

《物理与工程》微信公众号

继续滑动看下一个轻触阅读原文

物理与工程向上滑动看下一个

原标题：《怎样优雅地画驻波模型图和惠更斯原理图？》

阅读原文