应县木塔——千年前展示国人力学才智的十段柱五十五层梁摞接高层结构

建筑遗产研究

内容导读：应县本塔是在牛顿力学面世前631年就建成以木枋叠摞轻巧构架，形成人们可以登临其中敞亮享用的、完全符合结构静力学原理的高层塔楼结构。屹立至今已近千年，这在全球是唯一的，它展示出人类创造力的辉煌。本文基于结构力学基本原理，以对各类结构力性力理深切认知功底，通过反复思辩推理、系列立意设定，分析判断，最终从垛梁段柱摞成的八格巨筒中解算出塔架主结构梁柱在最不利负载条件下最大的内力、应力，裂缝深度、安全度，安全余度等相关数据。

文/李豪邦 张鹏程

1 概况

应县木塔如图1示，建成于公元1056年，为一概无螺栓铁箍、全由枋材叠摞，却存在70条上下全切断塔身的接缝。塔高54m（到主体顶）~67m（到塔刹顶），平面八角形由外边圈24根柱及内圈8根柱支持。平面的概略尺寸尺为：二层五层边圈（内圈）对角柱中心距分别为24.21（14.3）米。但在其边柱圈与内柱圈之间分上下两部，底部柱高2.8m（其内棚顶高3.6m）与中厅连通每层面积约500m2，该部外周无墙皆作隔扇门窗，故而通透敞亮、登上顶层高空观览令人神往。分层的上部为结构梁架的暗空间，其内并设了楼梯及过道。这里看得出此五米见方截面巨环空间的利用是十分巧妙得当。既衬托出中厅的高大森严，也使其外周信众社交活动间多了些温馨舒坦。通过这些结构布设说明我先祖匠师在设计高楼布设中是熟悉结构常理及其奥秘。

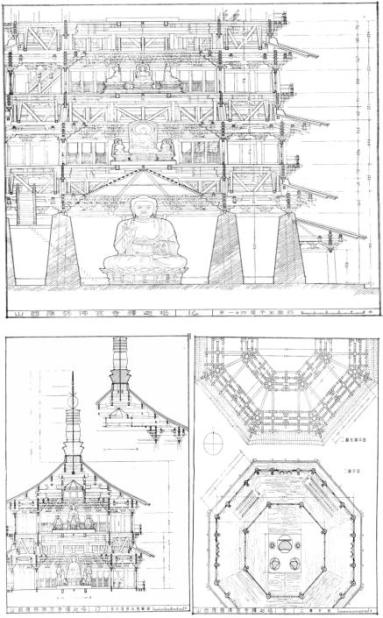
图 1 应县木塔结构测绘图

应县木塔进入当今学术研讨领域已逾90年，此中前40年是仅涉及建筑造型及内中设施布局，对结构受力的深入由于存在与当今结构设计惯理规则严重对立就出现了二难题：一是作为50多米的高楼其底层仅立32根顶底平接的柱。周边无硬墙，内无可抗侧力的构件，这从当今规则看这是机构而非结构，却抗了千年大风及多次地震，这该如何解释?其二是54m高的楼，其柱有长段2.8m，短段1.8m，段间设梁垛2.4m及、1.8m，层层依序摞接而成，实际的柱总长仅及楼高之半，这真类似儿童积木，可祖匠师就是有认知力理的信心建造成功，这力理究竟是哪些，这就使结构人士多是不敢轻易接触。再者也由于进行结构力学工作须备足条件，如荷载量值，用料尺寸及其强度数据及各部构造的细节关系，这些工作以个人能力是难以进行。应感谢陈明达、梁思成先生的前期工作，更感谢我国政府于1973年月29日下达指令后并拨款才得以全面展开。正是在此境况下通过交流查索互动联想大家认识到：千年前全球各地人们在追求建造高程中是应塔首先以逐件叠摞构架取代层层砌筑石条砖块建实体单实体塔是形成了人类推进建筑技术的一新里程碑。

此里程碑应塔必然生成在中华大地上，这是我国情和人文理念形成的。我国尊崇“己所不欲勿施予人”就没有奴隶。没有主体宗教就没有宗教战争与战俘。建造木质楼舍须有多类工具及成套知识技术；这就催生出专业经营建造的作坊，作坊内的技艺工其代代传承并研究改进发展，师徒中的精巧灵慧者通过在工作场地作简单比试，及在大风中亲手持件摆弄体会，甚至双手持木棍拟梁柱背后遭推，于其中领悟到木架结构在上部压重下传，及横来大风作用下、梁柱各件内生成拉、压、弯、剪、力偶、作用与平衡的感知、认知、熟知。对这些感知认知在作坊内形成口诀条规及至秘诀代代承传。正是他们中的佼佼者对高塔楼受风时，风剪力下传中生成“迎拉背压”转换机制具备了深切的力性力理认知，更加吸取汇集既往建塔楼的成败经验，他们才能完成应塔屹立至今，是完全符合力学长寿机理——“微歪抗风、底摆隔震”的伟绩。

与此并论，在西欧诸国由于连绵不断的宗教战争，就有了奴隶与战俘的劳动力，更怕建造木构楼舍会遭宗教对方一把火前功尽弃，故而兴建大型建筑是多用石构。他们在追逐比赛建造高度上，一律是用石材的实体、半实体塔结构，此类建筑经艺术设计绘图后无需用工程师作结构设计，只要有斧凿工具及奴隶劳动力即可行事。其中的力学要求仅是垫实与搭接，即使进入拱与穹只要厚大挤实即可。概无木质架构力理中须力偶平衡的繁缛奥秘。如意大利的比萨塔全高53.2m，下部墙厚3.2m。上部厚2.4m，除子有外表的装饰可供人赏识，其内却无可供人享用的空间。西方国家由于上述情况未能早期涉入建造高层架构楼的力学工作，故其高楼只能是在半顿力学面世后演进为可适用的结物静力学后，才相继于1883年在芝加哥建成11层的保险公司铁架楼，于1903年在法国建成钢筋砼的Franklin公寓楼。此二架构楼的出现是比牛顿力学面世分别晚了196年及216年，而应塔是比牛顿大学提前了631年。于此，我们可看出应塔应有的科技文化历史价值：今仍巍然屹立的应塔是全球早出了800年的首幢高层架构楼。

2 力学计算

个人参予应塔力学计算是从2008年初彻底退休下来出于兴趣爱好起始的。自认自己借助参加大设计院工作55年来，精心手算过多类工业厂房，各类构筑物，研究过预制大楼结构及砌块结构、岩士工程，这使自己具备了丰厚的多类结构力性力理认知功底，遇难题敢于创新思路攻坚下去。再者我认为应塔既然已屹立千年，则其结构作法必然是符合静力结构学的基本原理，此原理是千百年来不论国内国外，皆相同，永不变。这样只要依据此基本原理，摆脱当今只适应砼及钢结构的简化理（如果柱联接只有刚接与铰居中轴的铰接，柱须由底到顶通设）的桎梏，在创新思路之下应是能破解前述的二难题。此顶工作的关键是不断推进思辨推理分析计算，甚至受阻时另辟新径；如对塔底明层无抗侧力难题，只要推翻“铰居中”规定，另创铰可随风摇移，形成上下反对称的合理格局、则“墩式柱”是会有抗风的能力。具体到应塔够不够则须经计算确定。另对上下断柱插入梁垛难题，首先结合实际从力学角度视该处确实是梁的嵌入端支座，同时又是柱的组成部分，据此可设定该部为“夹有五，六层枋梁的暗框架结构”，而后按塔体所受负载及风力作力学计算，若计算能通过，则说明设定是正确的，另也证实塔结构安全可靠。以下即依此进行计算。

2.1结构组成与计算取层

塔结构由五个结构单元层组成，其二到五每层层高8.8m。是由底起明层2.8m高的长段柱、2.4m高梁垛、1.8m高撑架短段柱、1.8m高上层梁垛，依次组成。结构的立面局部简图如图3示。其平面的梁柱布置可见图1，只是其中未示出拉结内外角柱的八处辐射向梁。以下计算取第二层为计算单元（按理应取底层，但由于依据的文[1]中绘出的柱长9.05m，推理明显属误，却无法落实，故如斯）

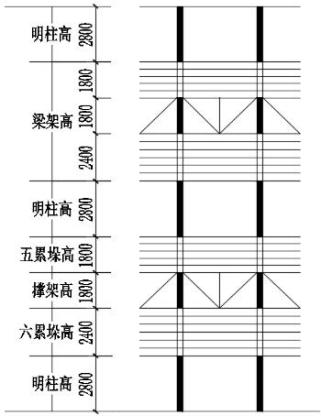
图 2 局部立面结构图

2.2风载

配合取第二层计算的粗泛，今简化风载计算为：考虑楼体下宽上窄，以及屋顶收尖，风压是上大下小，今按楼体上下同宽，为25m，风压上下等值90kg/m2、取屋顶高54m，底层高按文[1]取14.65m；则于第二层顶接收传来的风剪力V及风力矩M分别为：

V=25×（54-145-8.8）×90=62738kg=69t

M=69×（5.4-14.65-8.8）/2=1050T.M

风对第二层外周面作用的总风力W为：

W=25×8.8×90=19800kg=20t

2.3上部传下的静压重

据录繁兴陈四营著《古建筑保护研究》载：二层总受压力2015t，它是由32根柱合作承受，今计及各柱承担的面积大小不同，取外角柱承力为Nmax（最大压力），外面柱承力为Nmin（最小压力），此二的量值分别是均值N乘以系数1.5及0.8.则其值分别为：

均值N=2015/32=63t

最大值Nmax=63×1.5=95t

最小值Wmin=63×0.8=50t

2.4有关风力下传的力性力理机制

从图1的布局来看（若补绘出连接内外角柱的八向辐射梁则更清晰）梁柱的布设是相当严谨，以入个梯形格围合成外径25m的巨型八角筒，每折角都是三向梁的搭摞拉接，其交点正对上下段柱中心，这对塔结构整体、抗风的刚度、稳定是十分有利。今根据柱上下传力顺畅，虽然全高有70道水平切缝，只要下传的力能足够大，梁就是能嵌固在柱里形成框架。这是抗风能力的出处根源。风对塔体的作用是，随了位置的愈下，形成愈大的风剪力与风力矩，风剪力的下传不同于竖重力可无牵扯真贯下去，而是随了下传就生成新的力矩，须以其下承力结构的迎拉背压来了结。这里的迎拉背压，细想来看，是存在一种机制，就如足踩树下直角叉的横枝，手推竖枝，意欲掰直的生掰硬蹩。正是此塔体中梁枋与段柱间的生掰硬蹩，形成了可称是“令横风生竖拉压下传”的机制。对此机制须是彻底领悟并作计算证实。

2.5风载下应塔楼柱的内力计算

2.5.1从二层柱的受力确认暗框架的成立

对二层层高8.8m顶底点的定位，根据力学原则取反弯点，应是明层长段柱的中点。该处的传力只有轴向力N与风剪力V，此N包括上部楼体压重及上部风下传生成的竖拉压力。由前节2.2知，本层顶受的风剪力V是69t，力矩是1050t·m，此1050t·m的力矩,通过上层的强力转换，按材料力学理论是会形成本层柱群迎风侧受最大拉、背风侧受最大压、中和轴处为零。今为简化计，取迎、背侧各有四柱且相距23m来承担此转换作为。于此可知经转换后，迎、背侧角柱受的拉、压力N为：

N=1050/4×23=11.4t

将此11.4t与前节2.3中的静压叠加，即可知在风作用下柱轴力的相关值：

平均值 N=63t

最大值 Nma×=63×1.5+11.4=106t

最小值 Nmin=63×0.8-11.4=39t

这里Nmin是39t的压力，说明在大风中，上部的静载压重是能确保大风时结构中存在的整面接缝不会拉开，是十分稳当，其上部不会栽根头翻个。另外柱的平均受压63t是不小，其在下传过程中，会将塔柱中长及短段柱端与三向层层叠摞梁支座部构成，满足要求而有余的充分压实。这从受力角度讲，该处虽然是上下左右搭摞，却可称是实实在在上下传力的柱，而三向与其相交是真真切切的嵌固，此嵌固结合就成就了抗风时所需木质框架的力学能力要求。今考虑梁垛高域内无实柱的实况，称此框架为暗框架，则相邻二柱间每一条梁就是一榀暗框架（柱是左右共用），据此，从图1平面来看，每层外周梁有3×8=24根。内周梁及辐向梁各8根，此三者共24+8+8为40根。查竖向梁的层数计及普柏枋，是下6上5共11层，这样单个结构单元层具有40×11=440榀暗框架，考虑到抗风时平行风向的框架出力是全效，垂直风向者无效，45°斜交者有效率71%，今依此计算其总有效架数为275榀。

2.5.2计算暗框架

时暗框架抗风的力学机理，我们可从观察砼框架抗风工作中取得感知认识，今从图4（系由二柱多层框架中切取四反弯点之间的一段）看，当顶点承受风剪力V、层高为H时，通过计算可知，不论梁处于何位，其左右两端的端弯矩之和必等同V·H值，于此推论，当二柱间有 n条梁，且各梁端受弯最大应力皆达允许值［σ］，设梁截面为边长为b的正方形（其截面模量（抗弯抵抗矩）为b3/6）；则此时可允许V·H值如下：

VH=n·[σ]·b3/6

今结合应塔实际：n=275，H=880cm

[a]据文[2]中节3.1皆取为476/2=234kg/cm2

V=69t=69000kg

则69000×880=275×234×b3/6

据上式计算b=17.8cm。其前面模量=17.83/6=940cm3，今查文[2]中表6-1所列二层用料，推理可知梁宽为250高为180，其截面模量W=250×182/6=1350cm3，于此看得出：实有的W比所需的W是大出近50%。

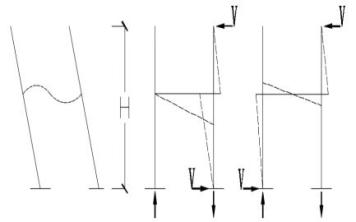
图 3 二柱单元框架抗风形变内力示意图

以上对梁架的计算表明：第二层结构单元在抵抗其上来风时，是仅用梁架中的梁垛部即完全有能力承担，且有近50%的富余，无需梁架中的撑架出面抗风。细品图3中梁工作的力性可看出，当风要推倒柱时，是固端的梁宁直不弯的硬蹩起了作用，此硬蹩的力构成了对图4中迎风侧柱的上挑受拉，及对背风侧柱硬按受压的局面，正是此梁内力操作特征，协同柱构成了塔屹立千年的伟绩。

2.5.3对梁垛柱段组合单元层柱的整体受力计算

柱的常规工作是受压，当抗风时会出受弯受剪工作，就受剪来看，二层所受风的总剪力为252（54-14.65）×90=88378kg，此力由32根直径54cm的柱承担，其生成的剪应力=88.538/32×π×272=1.2kg/cm2。其中，即使从接缝面抗剪来看，坡角为88.538/2150=4.1%，很小，无安全问题。对受弯，今取风力作用下受力最不利的迎背侧角柱计算，其所受柱顶来的风剪力值为25×（54-14.65-8.8）×90/32=2.156t，再还有本层外周的风力作用于本层高度的中点，其值为25×8××90/32=0.625t。以上二风力将生成柱底反力=2.156+0.625=2.78lt，此三力对柱的作用是要柱倾倒，此时上五下六的框架梁将提供力矩不允柱倾，此情况下每根梁提供的力矩值为=（2.156×0.8+0.625×44）/11=1.975t·m。为简捷计算，将五梁六梁作用的力矩各并为一力偶，M5、M6，其臂距取为各自部的全宽，则力偶M5、M6的力值N5、N6分别是N5=5×1.975/1.8=5.5t，N6=6×1.975/2.4=4.938t。将这些力值数据列入图4，经计算（此略）则得图4中的弯矩图，其最大值为3.89tm。于此须知，弯矩图中的值，仅是风力下传中“横（剪）转换竖拉压”过程中生成的内力，今要了解柱受力的全面情况，则尚须叠加其上传未的静压重及风生轴力。为此计算须由内力层面进入应力层面，今计算弯矩3.89tm生成的边缘应力（按直径54cm计）σ=389000/0.0982×543=25.2kg/cm2，将此叠加前节2.5.1的相关值即得生成于背（迎）风侧的最大（最小）应力分别为：

σmax=25.2+106000/π×272=71.7kg/cm2

σmin=-25.2+39000/π×272=-8.2kg/cm2

此最大应力71.7是远小于文[2]页110中的467kg/cm2之半。这表明受压的安全余度很大，而σmin为负值说明截面边缘出现了拉应力，为有力思辨此情况，今计算该面受压侧的边缘压力σ=25.2+39000/12=42.2kg/cm2，此计算表明压应力是拉动的约5倍，于此推理知：受拉离缝的深仅为直径54cm的六分之一，即9cm，而截面的受压区为45cm宽，这充分表明即使开裂9cm深。其截面受压拉都是安全可靠的。

计算至比可说是以脑智辟路、手写算画完成了静力的思辩推理分析计算，下步应是作抗震验算，但结合塔底层仅由32柱支持，概无抗侧力构件，其在屹立千年间，遭六次烈度6以上地震，最大烈度7~8，据此而论，塔是自隔震结构，故无须计算抗震。

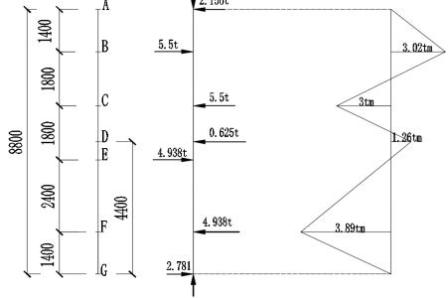
图 4 夹梁的段柱弯矩图

3 难得的珍贵收获

3.1计算古建结构（甚至一些创新结构、复杂难题）不能单用有限元，必须有脑智的思辨推理计算给出薄弱面目标

对古建结构作力学计算的基本要求是，给出主结构系统的最不利受力状况、薄弱环节、安全余度，以便于维护工作做深做细。对照我国从1973年起始要求计算50年来，特别是近三十年来，国家下大力推进计算，是出现了不少成果。但遗憾的是，由于都是独用有限元，这一囿于编程，有既定范畴，只能单方面运算，不能全方位工作，致使如巨著《应县木塔保护研究》虽用了近百页的幅面，也未能满足给出关键数据，将结构工作的力性讲清道理。应当承认有限元是很好的力学计算工具，须在脑智思辨协同下推理运用。否则它会以其表面显赫，可隐现高科技，更能轻松快捷地了结差事的诱惑力，在无知觉中形成严重差错（如对2008奥运四场馆设计中，个个都存在可称是违背力学基本原理的错误；另对一钢旋梯设计中，载入杂志2007-11钢结构中的竟比国家建筑标准设计“0ZJ401中的BLTB-B515”的用钢多浪费400%，而造价的浪费更是在1000%以上），于此看出单用有限元，将脑智技手艺排除是不妥。今后作设计计算应是脑智技胁助电算最好，此中会出现左右推敲的慢条斯理，艰苦磨蹭，但对国家事业有益，是值得的。

3.2 应塔的最大成就是以自身作了千年实验告示当今：风是施力、震乃输能，对楼体结构只要设计计算作好，就是既能抗风又可隔震

有关应塔底层用顶底平接柱形成文[3]述及的“摇移铰墩柱构架自隔震”作法，此类实例是很多。如在1976唐山地震中就喊出了“八柱支四梁重屋盖就是好，高烈度区可多用”。这里的八柱就是摇移铰墩柱。再有汶川地震中出现了如载于《建筑结构学报2011.5期第3页图4中，底层为砌块柱支持的五层楼，其震损是柱顶砌块被一层层压碎，致底半层逐次塌下，但其上四层却十分完好，竟连女儿墙顶的花盆都原位不动，这里底层砌块柱实质就是摇移铰墩柱构架机制。此外，从山野一些巨石其底支持面甚小的怪立，推理来看，都是千万年来屡遭震袭的遗迹。这表明“既抗风又自隔震”是自然现象之一。其之所以存在，是由于风是逐步进入、持之以恒、不能隔断的作用力，而震撞是必须瞬间完成的高速输能，是可以隔断的。这从对置于地面上的木板钉钉子来看出，用大力按钉、踩钉都难以入木，但举小锤击之则钉可进，这里反映出由于施力是慢动作，其反应的反力可完全聚集，而输能的撞击由于高速，瞬间来不及将反力聚齐，这就形成了反作用力小的缘故。此理亦可从枪弹打玻璃出孔而不裂，铝杯掉石面上杯出小坑，此二现象皆无法在实验室以静力的做法出现之事中说明，施力与输能二者就是不同。于此也可看出，输能是有“必须瞬间完成”的必要条件。对此仍可用钉钉子来领悟，即将木板置沙发软垫上，击钉则不进，这表明受体柔化即失去“必须瞬间完成”的必备条件，因而失去输能过程，起了隔震作用。千年应塔能隔震，其因即在底层相当柔化。无法完成“瞬间完成输能”，震时形成晃摆柱，起了隔震作用。

地震对结构的作用确实是异常复杂，它涉及震源与结构物的方向、关系、频数、幅值诸多因素难以有效应对。长期以来不少学者是采用橡胶隔震来解决难题。但此作法存在橡胶老化变质的寿命问题，再者用此法须多建一层地不室以放置胶块与梁架。就此而论，采用自隔震（有关砼隔震柱的作法可见文[5]中的图2）是极为简便。但采用自隔震，人们是存在“风与震皆为横向作用，自隔震结构真能隔去此留用彼吗”的顾虑。对此是难以讲清道理的，必须有实验证实。恰好的是，应塔以千年经历六次烈度6~8的地震作了实体实验，证实了只要设计计算周密，楼体结构就是能取得“微歪抗风、晃摆隔震”的兼得效益。于此可说，在人类运用结构自隔震的进程中，是应塔树立起了里程碑标志结构的贡献。

于此须补充说明一点，即以上所说自隔震其实只是隔断了地震作用中，地面对结构底都冲撞的直接作用，而对地震的间接作用，即自振聚能动力放大生成对相对细高的细囱、水塔、高耸架构之顶端上部的振冲作为则尚难定论。今在此基本了解塔力学工作机制之下，我古建界应是尽快将塔西南角六根歪斜过400mm的柱扶正，这是燃眉之急。其次考虑梁厚180是薄，宜将梁架中斜撑杆利用碳纤维布将其加固为拉压皆强的桁架杆为好，这可为实现学者葛家琪，柴晓明在文[4]中提出“应塔将能够屹立在新的千年”里垫底。再者，也应大力宣讲应塔的高技巧力性力理，让这座人们起始不敢想能抗风更能隔震的高水平结构物也进入世遺殿堂，与半实体（墙厚3.2~2.4m）全无技术含量的比萨塔平齐，而不是“低人一等”，只有这样，才能对得起祖先人民和国家。

后记

李豪邦先生此信写于2024年6月4日，寄信邮戳日期为6月8日。先生时年已94岁，在稿纸上边缘写道：“张教授：您好！呈您下文敬请指正为盼。写此文很不顺利，文研部门不给出石础墙的实情，对2010发表的初探应塔力学机理一文也概不置许。因已聋就失去了与学友的切磋提高，老伴更是因我耳目衰退恐瞎恐瘫，隔断对外连系，不告我来电话实情，只是管不了我去省市图书馆，写算，才能完此拙作，算是了却一番心愿。李豪邦 2024.6.4”

先生手书字小，交予打字员打来的初稿错误颇多，我又逐字改正。待读完全文，不由得肃然起敬，先生表述准确、计算准确，行文严谨，所思所想集毕生工程实践经验与思考，其结构计算简图的提取，及其计算结果，与显明的自然现象及本原的自然规律可相映证而吻合。我只是打印校对，对原文一字未改。

——张鹏程 2024年7月28日

参考文献

[1] 陈明达、应县木塔[M]。文物出版社，2001

[2]侯卫东、王林安、永昕群，应县木塔保护研究[M]，文物出版社2016

[3]李豪邦。初探应县木塔屹立千年的力学机理[C],工业建筑增刊2010

[4]葛家琪,柴晓明,刘金泰,不可移动文物安全稳定风险防控现状与思考-以应县木塔为例[J]，中国文化遗产

[5]李豪邦，梁云峰，建筑震害的主导物理量应是地面动位移速度的反复冲撞输能[C]。工业建筑增刊2018

（本文作者：李豪邦，中国建筑东北设计研究院原副总工，撰稿时年94岁；通讯作者：张鹏程，博士，厦门大学建筑与土木工程学院副教授，主要从事结构工程研究）

（本文经作者授权刊载，中国民族建筑研究会信息宣传部整理、编辑，更多精彩内容敬请期待下期。电话：010-63261268）