下载客户端

这恰恰就是数学之所以是数学

2024-08-14 11:38

来源：澎湃新闻·澎湃号·湃客

数学可以被定义为一门学科，在这门学科中，你永远不知所言为何物，也不知所言之物是否为真。

——罗素

选自《数学的雨伞下》

1901 年，英国逻辑学家伯特兰·罗素（Bertrand Russell）发表了一篇文章，他在文中写道：“数学可以被定义为一门学科，在这门学科中，你永远不知所言为何物，也不知所言之物是否为真。”这一评价既清晰又生动。罗素不仅没有将数学的不确定性视作有害的，而且还字字句句地大声宣告，这恰恰就是数学之所以是数学！

而我们可以相信罗素的话，他知道自己在说什么。罗素对数学的根柢了如指掌。在写下这句话十年后，他与同仁阿尔弗雷德·诺思·怀特海（Alfred North Whitehead）合著了《数学原理》（Principia Mathematica），他在书中提出的公理奠定了数学作为一种统一的理论的基础。如果说，欧几里得用五个公设构建了整个几何学，那么罗素和怀特海就把整个数学囊括进了他们的理论中，从几何到代数，从牛顿使用的向量到康托尔集，甚至还有在撰写《数学原理》时尚未定论的理论，比如分形，都可以在两人的理论框架中得以构建。

总之，如果罗素说数学不知自己所言为何物，那么我们可以通过倾听数学的所言之物得到诸多启发。此外，只要仔细想一想，你就会觉得这并不让人感到意外。这场旅途中的一些线索，应该让我们心怀警惕。模糊在数学中扮演关键角色，已有时日。

你应该还记得美索不达米亚的书吏及他们没有零和小数点的体系。他们也不知道自己所言为何物。在写下 12×8 = 96 时，他们说的可能是120×8 = 960 或 1200×80 = 96 000，又或是 0.12×0.8 = 0.096。模糊已经出现，书吏们不仅没有视之为妨碍，反而加以利用。借助这种模糊，他们理解了乘法的一个基本特性，而这一特性在后来又被纳皮尔及其所有后继者所利用。

数字的概念本身就带有不确切性。自打学者们让数字成为独立于计算对象而存在的虚构实体时起，他们就不再知道自己计算的为何物了。在写下 2 + 3 = 5 时，你并不知道这是在加巧克力、千米、书，还是什么都没加。但这个等式是正确的。

阿根廷作家豪尔赫·路易斯·博尔赫斯（Jorge Luis Borges）在1942 年发表的短篇小说《博闻强记的富内斯》（Funes el memorioso）中讲述了一个年轻人的故事，这个年轻人因为拥有超群的记忆力，所以无法忽视其他人无法看到或觉得无关紧要的众多细节。超群的记忆力非但没有成为一种优势，反而因为主人公无法意识到自己所见世界的不同之处，很快变成了严重障碍。这个年轻人无法用同一个词来指称不同的事物，他很难接受在某一刻从侧面看到的一条狗和一分钟后从正面看到的一条狗具有相同的名称。博尔赫斯写道：思考，是忘记差异，是概括、抽象。无法忘记的富内斯也就无法思考了。

模糊的关键在于不变的概念。对象各有不同，但由于存在共同点而理应具有相同的名称。情况各有不同，但可能以相同的方式运转。研究这些共同点和运转方式，相当于一下子想到千百种不同的事物，却不知所言为何物。这么做绝非徒劳之举，而是一个丰富的过程，可以引导我们对世界具有全面和深刻的了解。

我们所说的模糊、不精确或模棱两可，实际上有一个我们已经知道的名字：抽象。字词对我们的影响大到令人难以想象。你看，我们之所以不认得“抽象”这个旧相识，只是因为叫法不同。它不应该让我们感到害怕。正是它，自我们开始探索宇宙的内部运转机制以来，就一直支持和陪伴着我们。

抽象这只怪兽比我们到现在为止所能够想象的要强大得多。从一开始，模糊就在那里。模糊不是毫无预兆地冒出来的，它在数学思维的发端就站在了我们面前。然而，学会认清模糊，并意识到模糊王国的规模，还需要很长一段时间。

抽象之于观念就像什锦蔬菜之于蔬菜：一种将多个不同之物集合在统一名称之下的方法。此外，“什锦蔬菜”（macedonia）一词源自希腊半岛东北部的一个地区（即马其顿，Macedonia），那里以多民族混居而闻名。因此，抽象推理的先驱之一——亚里士多德在那里诞生也就不足为奇了。

公元前 4 世纪，在国王腓力二世的推动下，马其顿王国经历了一段繁荣期。腓力二世进行了数次改革，并在公元前 338 年的喀罗尼亚战役中征服了雅典和底比斯，从而成为希腊的统治者。亚里士多德于公元前 384 年出生在斯塔基拉，这是最早被马其顿王国征服的城市之一，位于斯特里蒙湾的海岸。腓力二世对这位学者颇为赞赏，并把自己的儿子，也就是未来的亚历山大大帝托付给他教育。

后来，亚里士多德倾其一生创作了一部令人叹为观止的著作，这部著作产生了巨大的影响。事实上，它的影响太过巨大。亚里士多德的许多错误将被反复教授，在数百年间从未受到过任何质疑。他以地球为宇宙中心的理论在很长一段时间里阻碍了哥白尼、开普勒和伽利略的思想的问世。

在亚里士多德的众多著作中，我们可以特别关注一下《工具论》。这是一本论述推理和逻辑艺术的文集，尤其阐述了从假设中得出结论的不同规则。这些规则被称为“三段论”。以下是最著名的三段论之一：

凡人皆有一死；

希腊人都是人；

因此，希腊人皆有一死。

你肯定同意这个推理是完全正确的。你也可以通过直观地描述凡人、人和希腊人来说服自己相信这一推理（图 4.12）。

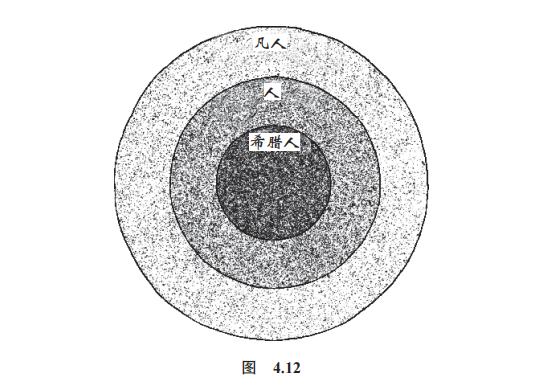
显然，“希腊人”包含在“人”的圈子里，“人”又包含在“凡人”的圈子里，“希腊人”除了也是“凡人”之外别无选择。要理解亚里士多德的推理方法，就必须区分推理的正确性和所陈述事实的正确性。

比如，让我们来看看下面这个新的三段论：

所有的哺乳动物都有鳞片；

鹦鹉是哺乳动物；

因此，鹦鹉有鳞片。

这几句话是完全错误的，但推理却是正确的！再仔细看看这三句话，你会发现，最后一句的确是前两句的逻辑结果。要说一个推理是正确的，则意味着其结论在逻辑上是基于其假设的。但是，当然了，如果假设是不确切的，那么结论也是不确切的。

在对三段论的研究中，亚里士多德关注的不是假设的正确性，而是推理的正确性，而后者并不取决于谈论的对象。换句话说：你不一定要知道所言为何物，就能进行正确的推理。上述两个三段论完全可以简化为下面这种形式：

任何玩意儿皆为东西；

家伙皆为玩意儿；

因此，家伙是东西。

你看，这是一个完全正确的推理。你无须知道什么是“玩意儿”“东西”和“家伙”，那是多余的信息。无论你赋予这三个词什么意思，如果两个假设都是正确的，那么结论也必然是正确的。而这不仅适用于这个特定的三段论，而且适用于所有有效的推论。

想象一下，有两个人正在看以上推理。对第一个人，我们告诉他“玩意儿 = 人，东西 = 凡人，家伙 = 希腊人”。对第二个人，我们告诉他“玩意儿 = 矩形，东西 = 四边形，家伙 = 正方形”。即使这两个人所说的不是同一件事，但他们都会同意这个三段论的说法。我们面对的就是一个误解（图 4.13）。

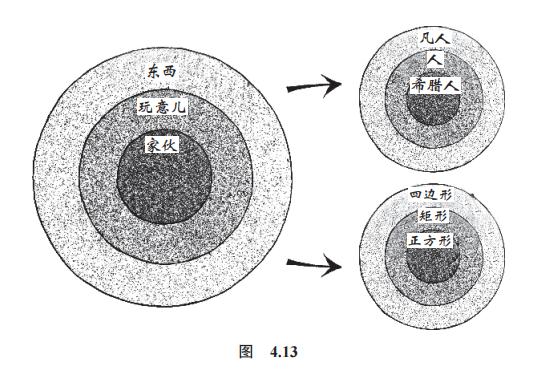
现在，让我们回到一个熟悉的例子上：欧几里得的《几何原本》。书中的五个公设说的是点、线、圆、直角和平行线，但假设一个人为这些词赋予了不同的含义，他会对此有所察觉吗？根据亚里士多德的说法，这对证明的正确性不会有任何影响。无论我们对欧几里得所用的词汇做出怎样的解释，他的论据本身都是正确的。

为了很好地理解这个原则，让我们重写一下五个公设，但要用更为模糊的字眼：

1. 从一个东西的任意玩意儿到另一个玩意儿可引且只能引一条家伙；

2. 任意有限的家伙可沿这个家伙无限延长；

3. 给定任两个玩意儿，可以一个玩意儿为心、到另一个玩意儿为半径作那啥；

4. 所有杂乱都彼此相等；

5. 给定一条家伙，通过此家伙外的任何一个玩意儿，有且只有一条家伙与之平行。

你看，我们完全不知道所言为何物了。现在想象一下，一个人为“玩意儿”“东西”等词赋予了不同的含义，但在他的阐释中，五个公设仍是正确的。那么，你可以把欧几里得的整本《几何原本》都念给他听，他绝对不会提出任何异议。因为对这个人来说，最初的假设是正确的，既然欧几里得的推理是正确的，那么我们所说的不是同一件事也就无关紧要了，结论在这个人看来是正确的。

换句话说，哪怕你对这基本的五个公设有“误解”，也足以继续后面所有的定理及其证明。只要为遵循五个公设的词语找到一种新的阐释，你就可以像几何学家一样放心地在这些公设中引用欧几里得的结论了。

任何数学都受到这些潜在误解的影响。它们既令人不安，又异常强大。它们为我们提供了新的视角，从而拓宽了我们的视野。如果有可能以不同的方式去理解欧几里得的用词，那么谁又能知道，这些阐释之一在某一天能否阐明第五公设呢？

推荐阅读

作者：[法] 米卡埃尔•洛奈（Mickaël Launay）

译者：欧瑜

法国数学学会“达朗贝尔奖”得主新作

数学，是理解世界本质与万物关联的工具

撑开数学之伞，享受思考之趣

《数学的雨伞下》

作者：[法] 米卡埃尔•洛奈（Mickaël Launay）

译者：欧瑜

惊讶！是思考的起点；

数学，是理解世界本质与万物关联的工具！

以数学为起点，以思考为快乐！

法国数学学会“达朗贝尔奖”得主科普名作。

数学，是理解世界本质与万物关联的工具，它能制造两个指南针：一个叫“实用”，一个叫“优雅”。不懂得数学的意义，就无法真正学习和理解数学。

科学家为什么那么聪明？因为他们有非凡的思考方法。

以数学为工具，以思考为快乐；培养自己的思考力、观察力，成为真正的思考者。

===============

科学，人类引以为傲的智慧结晶。而改变时代、推动历史进程的大科学家们，如同智慧之光，照亮万古长夜。

而数学家高斯说：“数学是科学的女王。”物理学家爱因斯坦说：“数学受到高度尊崇的另一个原因在于：恰恰是数学，给精密的自然科学提供了无可置疑的可靠保证，没有数学，它们无法达到这样的可靠程度。”

数学是宇宙的语言，从厨房的水龙头到使电视机正常播放的家庭卫生，甚至在路边买菜，数学无处不在。今天，信息技术已经被广泛应用到生活每一个角落，而这些成果的幕后英雄，正是数学！

因此，伟大的数学家，被载入史册，永远被后人铭记。今天推荐的20本数学家相关著作，不仅仅展现他们在伟大时刻的思考，也同时贯彻着他们一生的思维方式，这将成为所有人的宝藏。学好数学的前提，是学会数学的思维。

《改变世界的17个方程》

作者：[英] 伊恩•斯图尔特

译者：劳佳

•英国数学科普名家伊恩•斯图尔特经典名作，译为多国语言

•李永乐推荐科普名作，“欧拉图书奖”获奖作品

•美国数学学会（AMS）&美国数学协会（MMA）联袂推荐

了解世界运转的深层道理，看懂科学发展的规律

方程是一首首数学的诗，言简意赅，却充满意义。阐释自然与社会现象，连接数学与物理现实，是方程的力量与美之所在。

《数学那些事：伟大的问题与非凡的人》

作者：威廉·邓纳姆

译者：冯速

无需动用纸笔，纵览数学世界不可不谈的伟大定理、难题和争论；好奇心大满足，纵览数学的核心知识和历史八卦。

本书是一部短文集，文章以各自英文标题的首字母按照A到Z的顺序排列，每一篇短文都讲述了一个特定的数学主题，介绍了数学世界不可不谈的伟大定理、难题、争论和不解之谜。

《微积分溯源：伟大思想的历程》

作者：戴维·M. 布雷苏

译者：陈见柯林开亮叶卢庆

从古希腊、古埃及、古印度、中国和欧洲等地的微积分思想，到牛顿、莱布尼茨、伯努利兄弟、黎曼等伟大数学家的辉煌成就，看一看微积分这座“数学宝藏”是如何被塑造成今天的模样的。

《微积分的历程：从牛顿到勒贝格》

作者：邓纳姆

译者：李伯民汪军张怀勇

本书荣获“第七届文津图书奖推荐书目”。

这不是一本数学家的传记，而是一座展示微积分宏伟画卷的陈列室。书中的每一个结果，从牛顿的正弦函数的推导，到伽玛函数的表示，再到贝尔的分类定理，无一不处于各个时代的研究前沿，至今还闪烁着耀眼夺目的光芒。

《不可能的几何挑战：数学求索两千年》

作者：大卫•S. 里奇森

译者：姜喆

数学历史新角度，作者旁征博引，发掘了之前数学书未曾留意的历史细节。

本书以数学史上四大著名的“古典问题”——化圆为方、倍立方、作正多边形、三等分角为基础，展现了两千多年来，数学家们为解决这些问题而留下的令人拍案叫绝的思想与成就。

《贝叶斯的博弈：数学、思维与人工智能》

作者：黄黎原

译者：方弦

法国数学类科普书、大学数学参考及教材类图书畅销书目，在机器学习、人工智能、逻辑学和哲学等众多领域中，探索贝叶斯定理蕴藏的智慧与哲理。

贝叶斯定理一旦与算法相结合，就不再是一套枯燥的数学理论或认识论，而变成了应用广泛的知识宝库，催生了众多现代数学定理，以及令人称道的实践成果。

《代数的历史：人类对未知量的不舍追踪（修订版）》

作者：约翰·德比希尔

译者：张浩

更严谨、更翔实、更好读，全面展现代数自诞生至今的面貌。

这是一部恢宏的数学史和人类思想史，一本阐明代数基本知识的“数学入门书”，一册数学家的趣味故事集。

《最后的数学问题》

作者：马里奥·利维奥

译者：黄征

畅销世界的数学哲学史经典著作，科学和哲学巨匠们充满智慧的传奇故事，数学、物理、天文学和哲学的恢弘历史画卷。

本书讲述了数学概念的演化过程，引经据典地从哲学、历史、文化角度全方位地探讨了数学的本质，揭示了数学与物质世界、与人类思维之间的微妙关系，讨论了困惑几代思想家的重大问题，讲述了数学、哲学和物理学巨匠们的生活经历与思想。

《悠扬的素数：二百年数学绝唱黎曼假设》

作者：马库斯•杜•索托伊

译者：柏华元

牛津大学数学教授，英国皇家学会研究员马库斯•杜•索托伊科普力作，带你一同探索黎曼假设，讲述数学家求知路上的苦与乐。

黎曼假设，即素数的未解谜题，被视为数学研究的“珠峰”，吸引了一代代数学家投身于数论研究中，其中不乏数学史上大名鼎鼎的人物。而破解这一谜题过程中的发现，已经给电子商务、量子力学和计算机科学等领域带来了举足轻重的影响。

《世界是概率的：伊藤清的数学思想与方法》

作者：[日]伊藤清

译者：刘婷婷

伊藤清是如何学习和思考数学的？

数学家如何看待“纯粹数学与应用数学”“直观与逻辑”？

现代概率论是如何一步步发展起来的？

沃尔夫奖、高斯奖得主，现代随机分析之父日本数学大家伊藤清

讲述数学思想与方法激发关于概率与世界的深层呈现日本数学发展的另类线索

《数学与创造：广中平祐自传》

作者：广中平祐

译者：逸宁

菲尔兹奖、日本学士院奖、日本文化勋章得主日本数学大家广中平祐亲笔自传

作者以解决“奇点解消问题”的故事为线索，讲述了自己如何学习数学、走上数学研究道路的历程，分享了在挑战数学难题过程中的思考方法与感悟，并就“数学与创造”“创造与情绪”“分析与大局观”等话题做了深入阐述。

《春夜十话：数学与情绪》

作者：冈洁

译者：林明月

天才数学家的极意文集、影响几代人的不朽名作。

本书从“情绪与心智”的角度，论述了认知发展、义务教育中的深层问题，同时阐述了对人性的细微考察与独到理解，是一本影响了日本几代人的经典名作。

《一个定理的诞生：我与菲尔茨奖的一千个日夜》

作者：塞德里克•维拉尼

译者：马跃杨苑艺

畅销世界的当代数学家传记，知名数学家塞德里克·维拉尼荣膺菲尔茨奖的精彩历程，真切感受数学研究生涯的艰辛与乐趣，了解数学家的日常工作与思维方式。

《牛顿传：科学天才的浮生一梦》

作者：詹姆斯•格雷克

译者：欧瑜

文津奖获得者、科普作家、百万级畅销书作者詹姆斯·格雷克所著传记，故事、历史与科学的结合，展现牛顿辉煌的科学成就，剖析其鲜为人知的内心世界。

在这本传记中，格雷克借助牛顿的重要信件和未出版的笔记，记述了这位科学界最伟大人物之一的生活经历、与他有关联的人物，以及对他产生影响的重要事件，并勾勒出他所处的历史时期的全貌。

《我只会算术：小平邦彦自传》

作者：[日]小平邦彦

译者：尤斌斌

小平邦彦“抄书学数学”的传闻是真的吗？宽松的教育，是否会影响思考能力，又该如何改善？日本的现代数学研究是如何传承和发展的？

菲尔兹奖、沃尔夫奖、日本文化勋章得主日本数学大家——小平邦彦，亲笔自传

澄清“抄书学数学”之传言，评判日本“宽松教育”的利弊得失

还原“懒惰凡人”到“菲尔兹奖得主”的真实样貌

讲述小平邦彦的数学学习心得与感悟，展现日本数学与科学发展的隐性脉络

《一个数学家的辩白（双语版）》

作者：戈弗雷·哈罗德·哈代

译者：何生

英国数学家戈弗雷·哈罗德·哈代的经典名篇，被称为是“用优雅的语言对数学真谛进行了完美的揭示”。

本书是哈代于1940年写成的心得之作，展现了数学之美、数学的持久性和数学的重要性三大主题。

《一个应用数学家的辩白》

作者：[美]劳埃德•尼克•特雷费森（Lloyd Nick Trefethen）

译者：何生

1940年，哈代出版了《一个数学家的辩白》，这是一位领先的纯数学家对数学的沉思。82年后，《一个应用数学家的辩白》是一位具有哲学倾向的数值分析师的沉思，也是他的个人回忆录。作者在数值分析的工作中找到了极大的乐趣，但对它与其他数学领域的关系感到困惑。本书更准确的书名应该是《一个数值分析师的自白》，它包含更多的传记材料和更多的数学内容，尤其是在后半部分。但两本书的目的是相同的，都是从作者自己的角度对数学进行严肃的沉思。

物理学

《费曼传：天才的人生与思想世界》

作者：[美] 詹姆斯·格雷克

译者：高爽赵晓蕊

中国文津图书奖得主、美国国家图书奖得主詹姆斯•格雷克新作《费曼传：天才的人生与思想世界》，有趣的灵魂，天才的魔术师，科学家们的偶像，盛名之下理查德·费曼的真实人生。

他是天才，更是众人难以企及的“魔法师”，总有新点子来解决难题；

他凭着一股“超能力”，在游戏的精神和探索的智慧之间自如穿梭；

令人目眩的人生经历、率真的态度、永不枯竭的热情，他是科学家们的偶像；

……

这就是费曼——好奇的大男孩、多情的爱人、诺贝尔奖得主、原子弹制造者、“挑战者号”事故调查委员、邦戈鼓手、开锁大师……他为20世纪的物理学开辟了一条非凡的道路。从顶级科学家到满怀好奇的大众，在他参与的每一件事和接触过的每一个人身上，费曼都留下了非凡的印记。

教材

《复分析：可视化方法》