如何制定主题乐园的年卡价格

主题乐园的年卡（或会员卡，以下统称年卡）是游客购买的，在特定周期内（一般为1年）供游客本人无限次入园的凭证。年卡是主题乐园门票价格体系的重要组成部分，但是，年卡价格应该如何确定，价格高一些好还是低一些好，一直是困扰很多主题乐园行业从业人员的问题。对于年卡价格高低制定的依据有很多，比如为了平衡主题乐园的淡旺季游客量、为了构建主题乐园与游客之间的更加紧密的会员关系、为了向游客提供更好的会员服务提升乐园自身的吸引力等等。本文主要从主题乐园收入最大化的角度，通过定量分析的方式，来探讨主题乐园年卡的定价方法，以供大家参考和讨论。

▲

主编 | 杨明

责编 | 井翔远

作者 | 中国游乐特约作者 杨剑川

前提和假设

本文主要通过定量分析的方法来研究问题，有必要提出研究的基本前提和假设，不同的主题乐园可以依据自身的实际情况对相关的参数和前提进行调整，满足实际分析的需要。

1、关于基本参数的假定

我们假设主题乐园样本A，它的标准门票价格既定，为P票；每年到主题乐园A游玩的游客人数既定，为N人（注意是游客人数，不是人次数或入园量）；主题乐园A在没有执行年卡政策（不卖年卡）的情况下，经统计得出的一年重游率为α，备注：重游率=年入园总人次/游客人数（N人）-1；在有年卡政策情况下，经统计得出的周期内年卡游客平均入园天数为F；主题乐园A非年卡用户园内二消占标准门票价格的比例为β1；主题乐园A年卡用户园内二消占标准门票价格的比例为β2。

假设以上参数均为统计常量或既定常量，只和一个主题乐园本身的产品特性和所处的环境相关，在分析过程中不随着自变量和因变量的变化而改变。

2、关于变量的假定

我们研究的核心是年卡价格高低的变动对于总收入的影响，首先研究关于年卡价格变动如何影响购买年卡的游客的比例问题，假定：

自变量x为标准门票价格占年卡价格的比例，即：

x=标准门票价格/年卡门票价格，自变量的取值区间为（0，1）

因变量f(x)为购买年卡的游客占总游客数量的比例，即

f(x)=年卡游客数量/游客人数，因变量的取值区间为（0，1）

3、关于变量的说明

在实践中我们可以明显感觉到，自变量x和因变量f(x)有着很强的正向相关关系，当自变量x取值靠近0，意味着年卡价格相对于门票价格来说非常贵，这时候将会导致购买年卡的客群大幅减少；而当自变量x取值越来越靠近1，意味着年卡价格相对于门票价格来说变得比较便宜，这时候购买年卡的游客将会不断增多。而x和f(x)的取值都不能小于0，因为价格没有负数，也不能大于1，因为现实中年卡价格不可能低于门票价格。

模型的建立

1、通过回归分析找到x与f(x)的拟合函数

关于x与f(x)之间的拟合函数，我们首先可以做一个思想实验：当年卡的价格非常高，高到游客购买一张年卡的价格可以覆盖全年每天都来主题乐园游玩的散票价格，这时几乎任何一位游客都不会选择购买年卡，这意味着x取值趋近于0，f(x)也趋近于0；而随着x值的增大，f(x)的值将会随之增大，但是一开始，f(x)增大的速度不会很快，因为年卡还是太贵了嘛；而当x的增大超过一定区间之后，f(x)随之增大的速度将会快速的增加，因为越来越多的游客开始觉得购买年卡是划算的，而当x的增大开始接近1的时候，f(x)的增加的速度将会变得非常快，因为只需要在门票的基础上在加少量的钱就可以购买年卡了，而当x趋近于1的时候，几乎所有的游客都会购买年卡，所以f(x)也趋近于1，因为年卡的价格和门票价格一致了嘛。这种因变量随着自变量的增加，一开始增加速度比较缓慢，而后来增加速度大幅提升的关系，非常符合幂函数的关系，所以，在后边的回归分析中，我们应该主要选择幂函数进行拟合分析。

接下来，我们需要找到历史统计的自变量与应变量的对应数据，以主题乐园A为例，历史统计数据为：

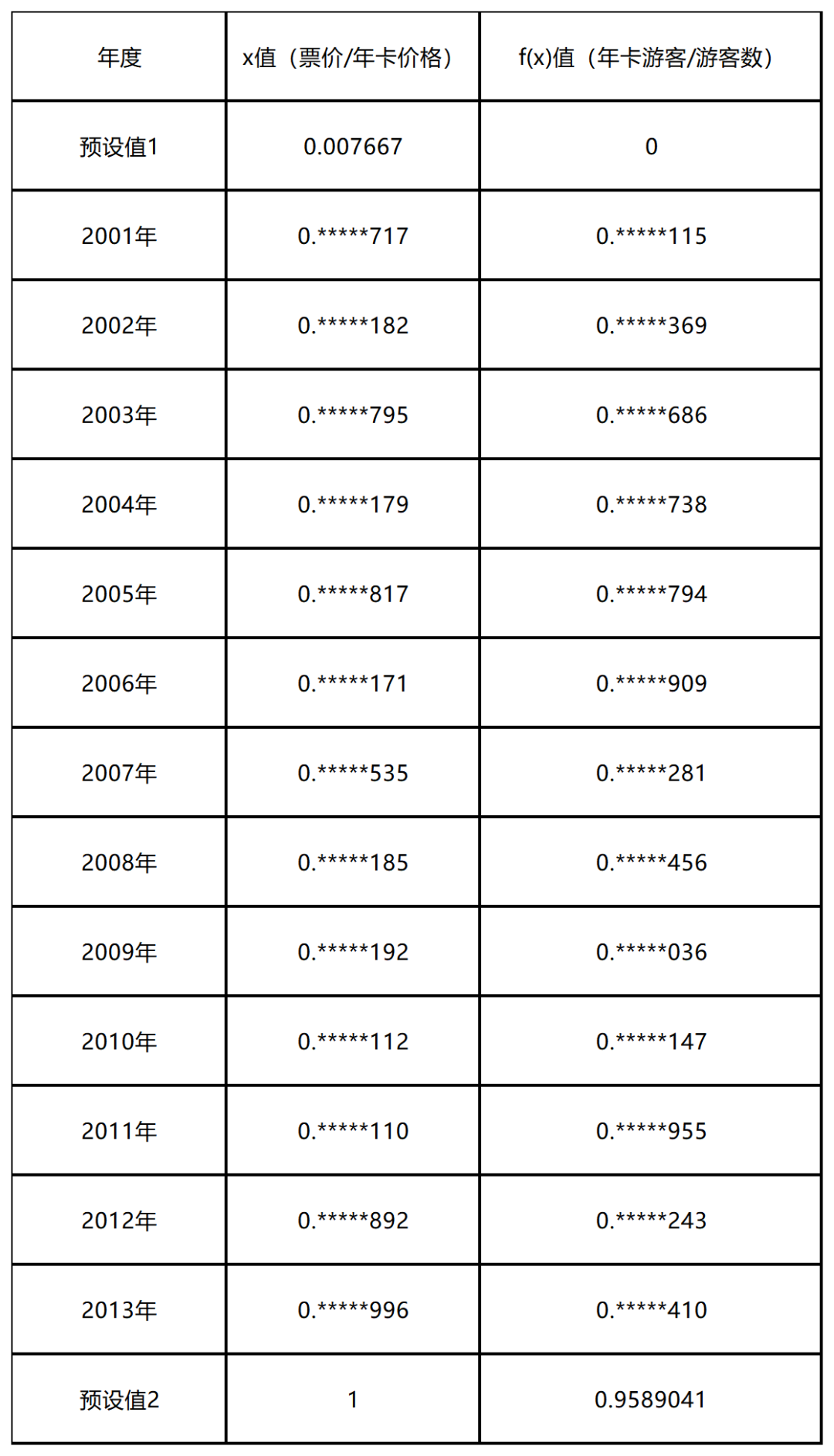
表1：主题乐园A历史价格比和年卡占比统计表

其中，样本数据的变化率越大越好，而预设值是按照我们上文的分析和假定，模拟当x取值趋近于0和1的时候的情况。有了样本数据，我们可以使用统计软件对自变量和因变量进行拟合分析，按照上边的分析我们选取幂函数进行拟合分析，如下图：

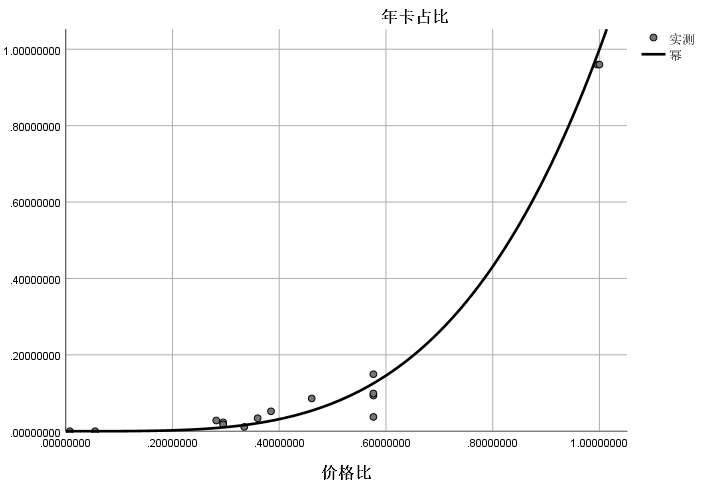
图1：拟合曲线

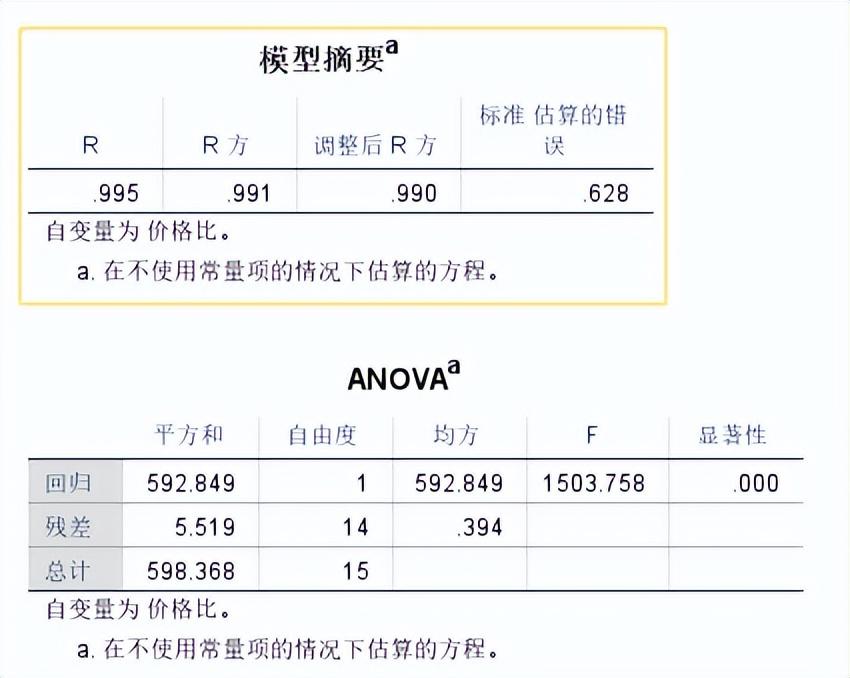
图2：拟合结果模型摘要

从拟合曲线和模型摘要来看，采用幂函数进行拟合的结果比较吻合，预测程度也很高，因此，通过统计软件，我们能够得出拟合方程（文中仅保留2位小数点，下同）：

f(x)= 1 * x^3.77，0＜x＜1

2、建立收入S与价格比x的回归函数

有了门票价格与年卡价格比x和年卡数量与游客数量比f(x)之间的函数关系，更进一步我们建立收入S和x之间的函数关系。

收入S由两个部分构成，一个部分是门票收入S1（一消收入），包括周期内销售非年卡游客门票和年卡；第二个部分是二消收入S2，包括年卡游客和非年卡游客入园后购买餐饮、商品和服务的收入，即：

S=S1+S2

而

S1=非年卡游客总购票收入+年卡销售收入

S1=P票*（N人-N年）+ P票*（N人-N年）*重游率α*（1-N年/N人）+N年*P年

将f(x)和x代入

S1=P票*N人*（（1- f(x)）+α*（1- f(x)）^2）+ f(x)/x））

其中：“P票”为标准票价，“P年”为年卡价格，“N人”为游客人数，“N年”为年卡人数，α为没有执行年卡政策情况下的一年重游率

而

S2=非年卡游客二消收入+年卡游客二消收入

S2=（N人-N年）* P票*β1+（N人-N年）* P票*β1*重游率α*（1-N年/N人）+N年*年卡入园频次F* P票*β2

同样，将f(x)和x代入

S2=β1*P票*N人*（(1-f(x)）+α*P票*N人*（1-f(x)）^2)+P票*N人*f(x)*F*β2

其中：F为周期内年卡游客平均入园天数；β1为非年卡用户园内二消占标准门票价格的比例；β2为年卡用户园内二消占标准门票价格的比例

所以：S1+S2合并后

S=N人*P票*（（1+β1）*（（1- f(x)）+α*（1- f(x)）^2）+f(x)*F*β2+f(x)/x）

模型的分析

1、找到对应最大收入的年卡定价

有了关于S和f(x)、x对应的函数关系，我们就可以通过求x在0-1这个区间上对应的S的极值点，来确定收入最大化的票价和年卡价格的比例了。

根据：

S=N人*P票*（（1+β1）*（（1- f(x)）+α*（1- f(x)）^2）+f(x)*F*β2+f(x)/x）

要求x在0-1这个区间上对应的S的极值点，因为N人、P票都是常数，所以其实就是要求（1+β1）*（（1- f(x)）+α*（1- f(x)）^2））+f(x)*F*β2+f(x)/x在（0,1）的极值点。

我们根据拟合函数

f(x)= 1 * x^3.77，0＜x＜1

将其代入（1+β1）*（（1- f(x)）+α*（1- f(x)）^2）+f(x)*F*β2+f(x)/x，并假定主题乐园A样本的α=30%，F=6，β1=20%，β2=5%

我们可以得到一个新的拟合函数

F(x)= 1.57-1.64*x^3.77+0.36*x^7.54+x^2.77, ，0＜x＜1

要求收入最大化的极值点，我们只需要对F(x)上求导，并令求导后的方程等于0，即：

F’(x)=0，0＜x＜1

通过观察函数图像的单调性所对应的极值点，我们就可以找到对应收入最大化的极值点

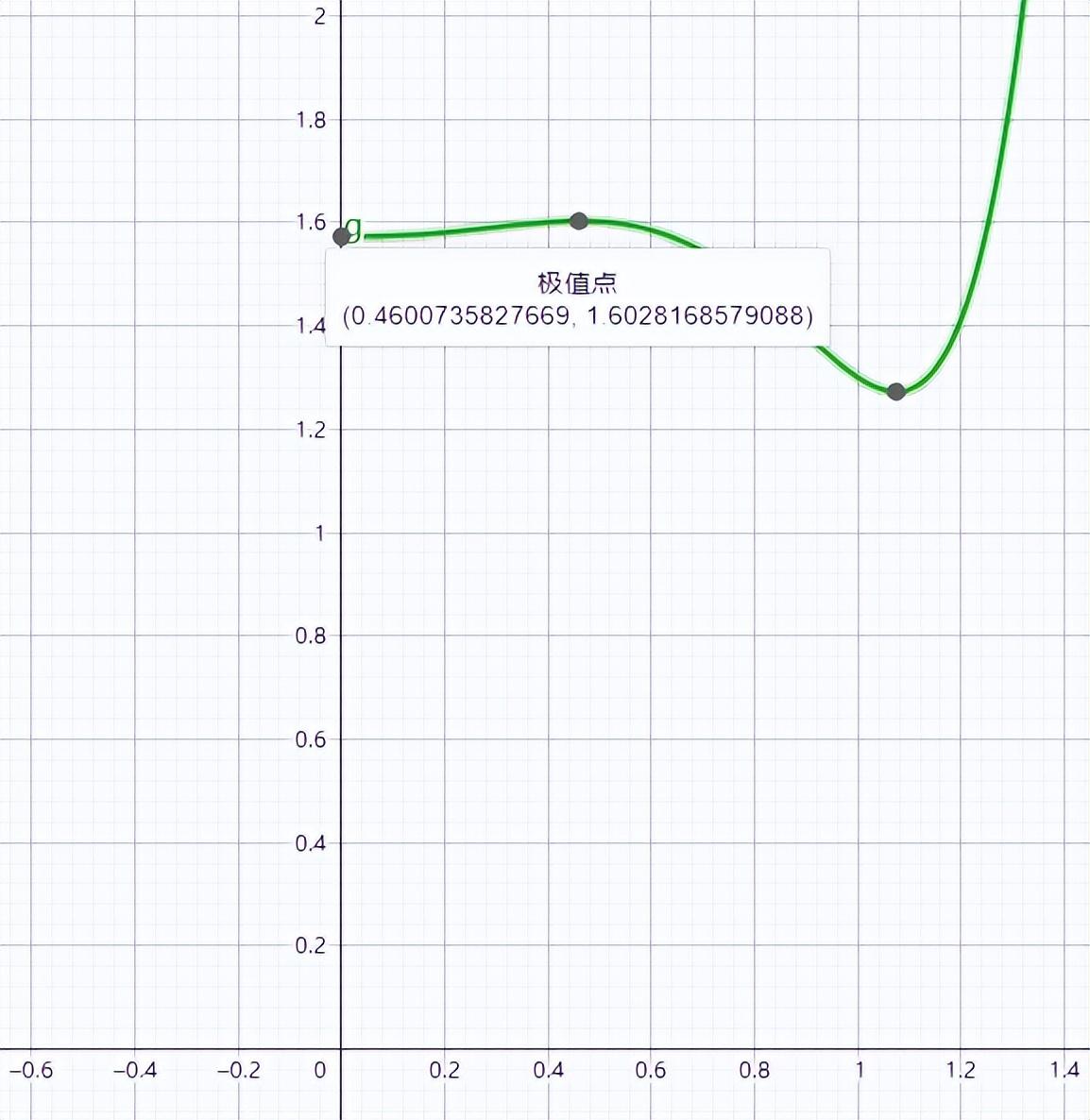
图3：F(x)函数图像和所对应的极值点

这表明，按照我们上述假设和参数建立的模型，主题乐园A收入最大化所对应的x值为0.46，即门票价格占年卡价格比例为46%，而在这个价格下，公园总收入达到最大化，系数为1.6。如果主题乐园A的门票价格为300元，那么年卡的价格应该为300/0.46=652元。

2、不同参数对于极值点的影响

在模型中，决定拟合函数的参数有重游率α、非年卡客群人均二消参数β1、年卡人均消费β2和使用频次F。这些参数的大小，是由一个主题乐园本身的产品和吸引力，客群特点所决定的。现在，我们探讨一下这些参数的不同取值对于拟合函数，特别是对于极值点的影响。

（1）重游率高低对于拟合函数的影响

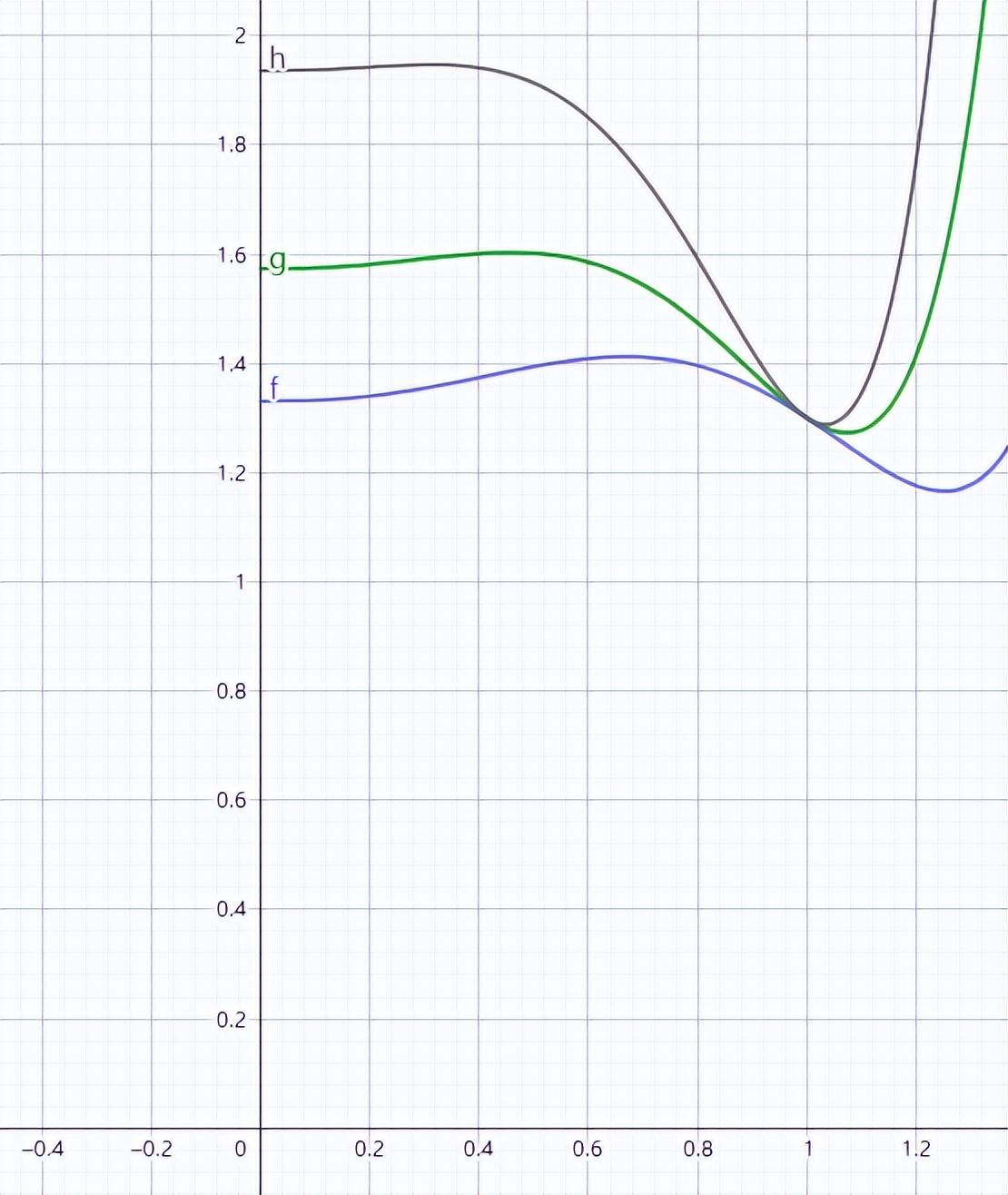
图4：不同重游率对函数的影响

在其它参数不变的情况下，通过模拟不同重游率，我们得到主题乐园A在重游率分别为10%，30%，60%所对应的极值点为0.67，0.46和0.31，随着重游率的上升，极值点x的取值向0方向移动，也就是说，如果一个主题乐园的重游率越高，相对应的年卡价格就应该越高，反之，如果重游率越低，所对应的年卡价格应该越低。

（2）非年卡客群人均二消参数β1高低对拟合函数的影响

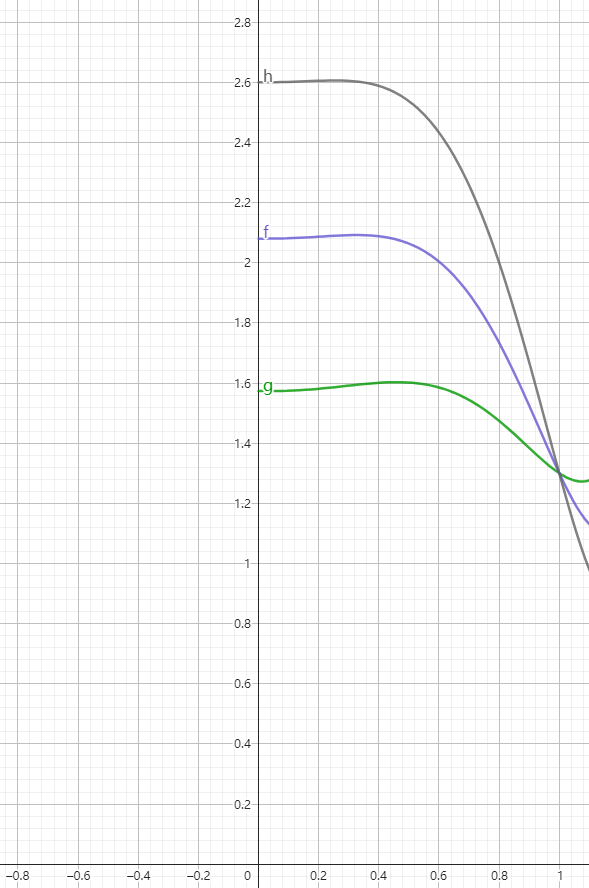
图5：参数β1高低对拟合函数的影响

参数β1代表非年卡用户在园区的消费与门票价格的比值，在其它参数不变的情况下，通过模拟不同β1值，我们得到主题乐园A在β1值分别为20%，60%，100%所对应的极值点为0.67，0.33和0.25，随着β1值的上升，极值点x的取值向0方向移动，也就是说，如果一个主题乐园的非年卡用户的消费越高，相对应的年卡价格就应该越高，反之，如果消费越低，所对应的年卡价格应该越低。

（3）年卡人均消费β2和使用频次F对拟合函数的影响

在F(X)函数中，β2和F值两个参数为乘积关系，所以我们可以使用β2*F的值进行统一分析：

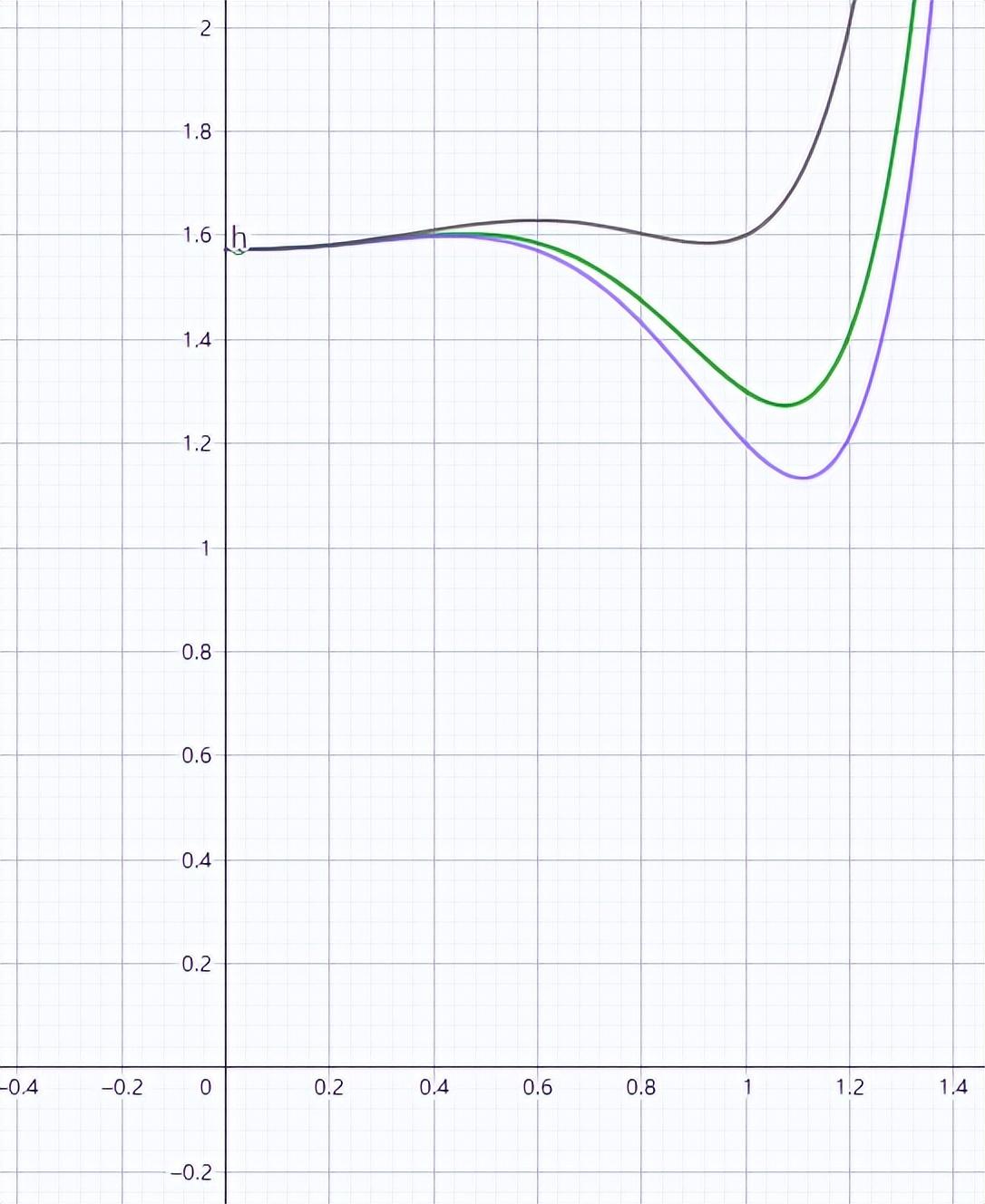
图6：不同年卡参数（F*β2）对函数的影响

参数F*β2代表着年卡客群在园区消费能力的高低，在其它参数不变的情况下，通过模拟不同F*β2值，我们得到主题乐园A在F*β2值分别为0.2，0.3，0.6所对应的极值点为0.43，0.46和0.59，随着F*β2值的上升，极值点x的取值向1方向移动，也就是说，如果一个主题乐园的年卡用户每一次在园区消费越高，相对应的年卡价格就应该越低，反之，如果消费越低，所对应的年卡价格应该越高。

3、拟合曲线形状对实际年卡定价的启示

按照上面的模型，一般来说，一个主题乐园（通过调研和数据收集）只要确定了模型中的相关参数，对于既定的门票和游客人数，我们就能够计算出令乐园收入最大化的年卡价格，但是，在实际工作当中，有很多数据是需要多年积累的，特别是确定变量x和f(x)相关关系的样本数据，如果是一个新开业的主题乐园，基本是没有这些数据积累的；其次，很多参数（如一年重游率，二消指数等）由于实际调研过程中，样本收集和数据收集的工作质量参差不齐，也可能导致相关参数的准确性存在偏离。在这些情况下应该如何应对呢？我们可以从拟合函数的形状出发进行分析：

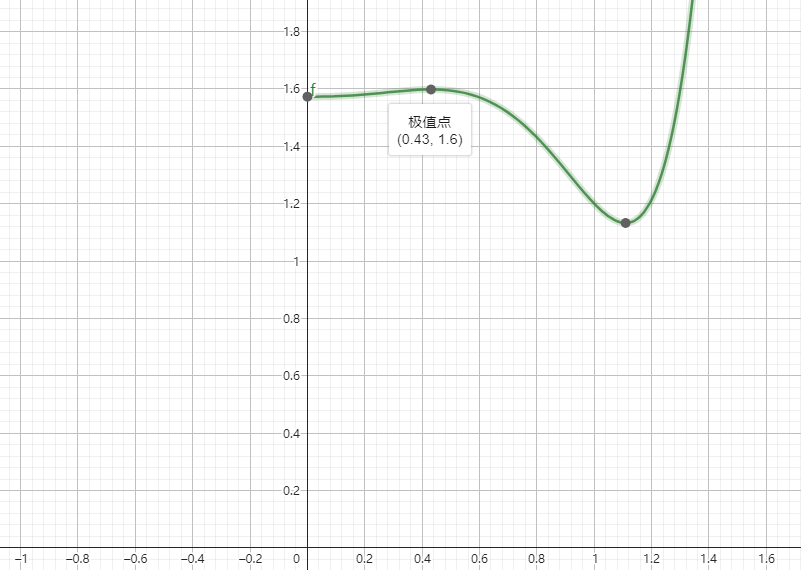
图7：拟合函数的形状

图7是一个典型的F(x)函数曲线，它代表着不同x的取值对于收入高低的影响，x值越接近0，年卡的相对价格越高，x值越接近1，年卡的相对价格越低。我们看到，x值在0到极值点（上图为0.43）的区间，曲线是相对平缓的，对过了极值点之后，曲线变得陡峭并往下走。而且通过模拟测算我们发现，不同的参数取值对于曲线的形状影响是比较小的。这意味着，只要是在0到极值点这个区间，对应的总收入变化并不会很大，在这个区间进行年卡价格的制定，总收入是有保证的，但是过了极值点，随着x的增大，总收入会受到很大的影响，如果在极值点到1这个区间定价，总收入很有可能会受到很大的影响。因此，如果一个主题乐园在数据收集并不准确或并不充分的情况下，可以选择尽量“贵一些”，这个区间是相对能够保证收入的安全区间。

实证分析

按照前文的方法，通过建立F(x)函数模型，我们就可以精确计算出收入最大化的年卡和门票价格比值，对于目前国内大部分主题乐园，x值集中在0.2-0.5区间，而且，吸引力越强，重游率越高的乐园，x值越小，这和我们模型的分析是一致的，见下表：

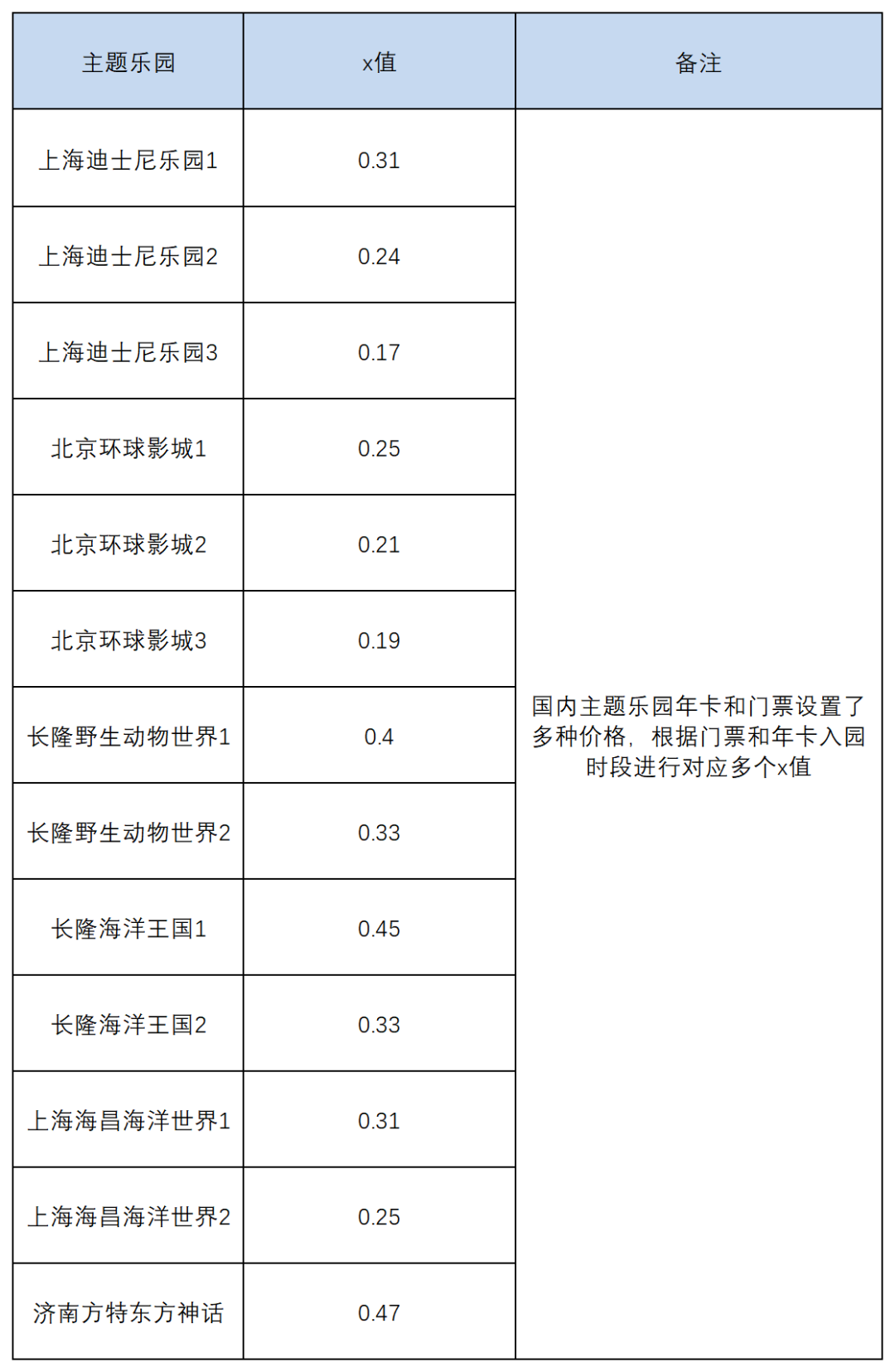
表2：国内部分主题乐园x值

结语

以收入最大化为前提，通过对样本数据的收集和回归分析模型，可以得出年卡价格变动如何影响购买年卡的游客的比例的函数关系，进而可以得出年卡价格高低的变动对于总收入的影响的函数关系，从而确定最佳的年卡价格。重游率，二消指数，年卡平均使用频次等参数取值对于模型极值点有着关键影响。在实践中，如果相关统计数据不够全面和准确，x取值在（0，极值点）区间是定价的“安全区间”。