深度神经网络压缩与加速技术

//

深度神经网络是深度学习的一种框架，它是一种具备至少一个隐层的神经网络。与浅层神经网络类似，深度神经网络也能够为复杂非线性系统提供建模，但多出的层次为模型提供了更高的抽象层次，因而提高了模型的能力。深度神经网络是一种判别模型，可以使用反向传播算法进行训练。随着深度神经网络使用的越来越多，相应的压缩和加速技术也孕育而生。LiveVideoStackCon 2023上海站邀请到了胡浩基教授为我们分享他们实验室的一些实践。

文/胡浩基

编辑/LiveVideoStack

大家好，我是来自浙江大学信息与电子工程学院的胡浩基。今天我分享的主题是《深度神经网络压缩与加速技术》。

首先一个问题是，为什么要做深度神经网络压缩？有两个原因：第一个原因是大型的深度神经网络很难部署在小型化的设备上。另一个原因是当深度模型越来越大，需要消耗的计算和存储资源越来越多，但是物理的计算资源跟不上需求增长的速度。

从右边的图可以看出，从2005年开始，硬件的计算资源增长趋于放缓，而随着深度学习领域的蓬勃发展，对算力的需求却是指数级增长，这就导致了矛盾。因此，对深度模型进行简化，降低其计算量，成了当务之急。近年来，以ChatGPT为代表的大模型诞生，将这个问题变得更加直接和迫切。如果想要应用大模型，必须有能够负担得起的相对低廉计算和存储资源，在寻找计算和存储资源的同时，降低大模型的计算量，将是对解决算力问题的有益补充。

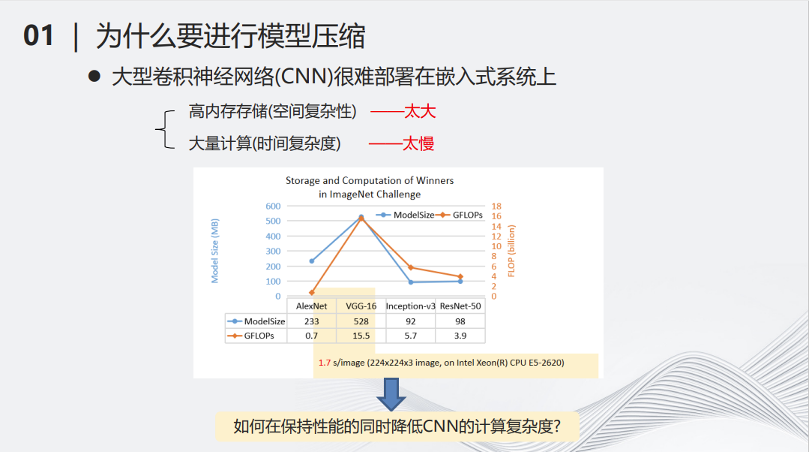
例如2017年流行的VGG-16网络，在当时比较主流的CPU上处理一张图片，可能需要1.7秒的时间，这样的时间显然不太适合用部署在小型化的设备当中。

深度神经网络的压缩用数学表述就是使用一个简单的函数来模拟复杂的函数。虽然这是一个已经研究了几百年的函数逼近问题，但是在当今的环境下，如何将几十亿甚至上千亿自由参数的模型缩小，是一个全新的挑战。这里有三个基本思想 -- 更少参数、更少计算和更少比特。在将参数变少的同时，用较为简单的计算来代替复杂的计算。用低精度量化的比特数来模拟高精度的数据，都可以让函数的计算复杂性大大降低。

深度模型压缩和加速领域开创人MIT的副教授韩松在2015年的一篇文章，将深度学习的模型压缩分成了如下的5个步骤。最左边输入了一个深度学习的模型，首先要经过分解（decomposition），即用少量的计算代替以前复杂的计算，例如可以把很大的矩阵拆成多个小矩阵，将大矩阵的乘法变成小矩阵的乘法和加法。第二个操作叫做剪枝（pruning），它是一个减少参数的流程，即将一些对整个计算不那么重要的参数找出来并把它们从原来的神经网络中去掉。第三个操作叫做量化（Quantization），即将多比特的数据变成少比特的数据，用少比特的加法和乘法模拟原来的多比特的加法乘法，从而减少计算量。做完以上三步操作之后，接下来需要编码（encoding），即用统一的标准将网络的参数和结构进行一定程度的编码，进一步降低网络的储存量。经过以上四步的操作，最后可以得到一个被压缩的模型。

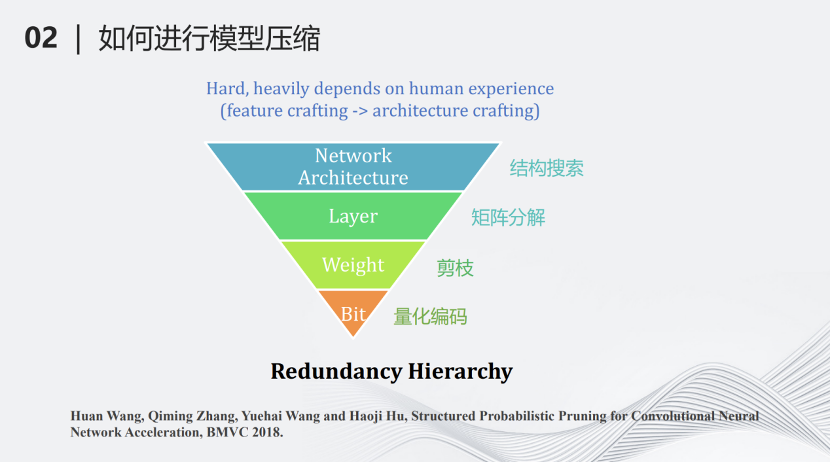
我们团队提出了另外一种基于层次的模型压缩分类。最上面一个层级叫做网络结构搜索（network architecture design），即搜索一个计算量较少但对于某些特定任务很有效的网络，这也可以看作另一种压缩方式。第二个层级叫做分层压缩（Layer）。深度学习网络基本上是分层的结构，每一层有一些矩阵的加法和乘法，对每一层的这些加法和乘法进行约束，例如将矩阵进行分解等，这样可以进一步降低计算量。第三个压缩层级是参数（weight），将每一层不重要的参数去掉，这也就是剪枝。最下面的层级是比特（bit），用量化对每个参数做比特层级的压缩，变成量化的编码。

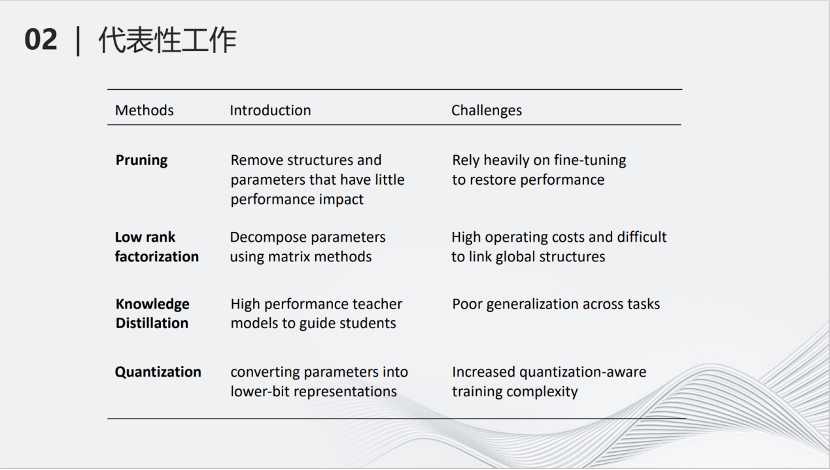
这里是各种压缩方式的介绍以及它们的挑战。剪枝（Pruning）减少模型的参数；低秩分解（Low rank factorization）将大矩阵拆成小矩阵；知识蒸馏（Knowledge Distillation）用大的网络教小的网络学习，从而使小的网络产生的结果跟大的网络类似；量化（Quantization将深度神经网络里的参数进行量化，变为低比特参数，降低计算量。

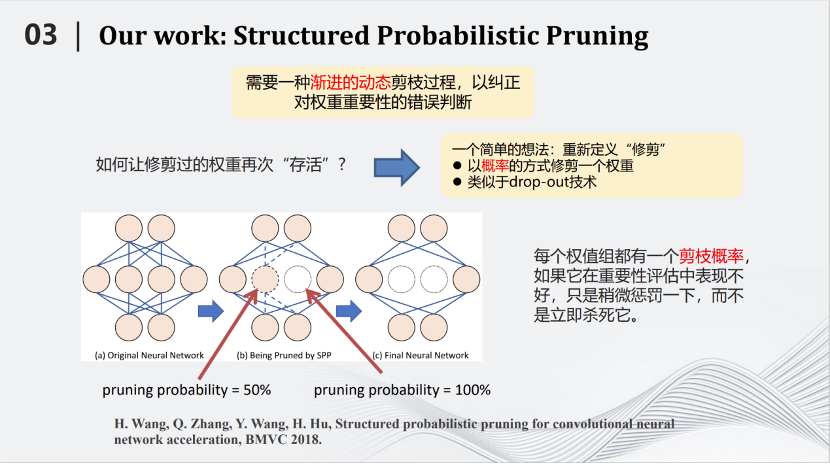
2018年BMVC会议，我们团队提出了一种基于概率的剪枝方法，叫做Structured Probabilistic Pruning。这种方法的核心思路是将神经网络里不重要的参数去掉。那么如何划分重要与不重要，是首要问题。最好的标准是去掉某个参数以后测试对于结果的影响。但是在整个网络中那么多的参数，如果每去掉一个参数都测试对结果的影响，时间就会非常漫长。所以需要用一些简单的标准，例如参数绝对值的大小来评判参数的重要性。但有一个矛盾是，简单标准对于衡量参数重要性来说并不准确。那么如何解决上述矛盾呢？我们提出的方案形象一点就是，用多次考试代替一次考试。我们将在训练到一定的地步之后，去掉不重要的参数，这个过程叫做一次考试。但是每次考试都有偏差。于是我们发明了这种基于概率的剪枝方法，将一次考试变成多次考试。即每训练一段时间测试参数重要性，如果在这段时间内它比较重要，就会给它一个较小的剪枝概率，如果在这一段时间内不那么重要，就会给它一个较大的剪枝概率。接下来继续训练一段时间，再进行第二次考试。在新的考试中，以前不重要的参数可能变得重要，以前重要的参数也可能变得不重要，把相应的概率进行累加，一直随着训练的过程累加下去，直到最后在训练结束时，根据累加的分数来决定哪些参数需要被剪枝。

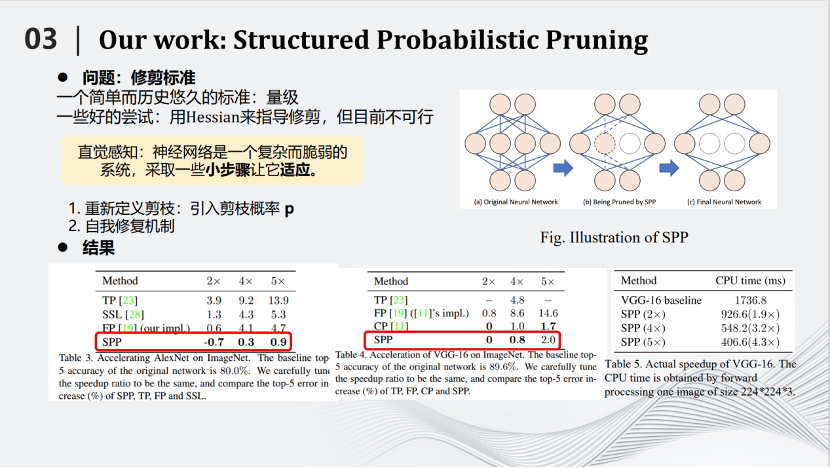
这种方式叫做SPP——Structured Probabilistic Pruning。SPP算法相对于其他的算法有一定的优势，具体体现在左边的图片里。例如我们将AlexNet压缩两倍，识别准确率反而提高了0.7，说明对于AlexNet这样比较稀疏的网络效果很好。从别的图片也可以看到，相对于其他的算法也有一定优势，这里不详细展开介绍。

2020年我们又提出一种基于增量正则化的卷积神经网络剪枝算法。通过对网络的目标函数加入正则化项，并变换正则化参数，从而达到剪枝的效果。

我们通过严格的数学推导证明了一个命题，即如果网络函数是二阶可导，那么当我们增加每一个网络参数对应正则化系数时，该参数的绝对值会在训练过程中会减小。所以我们可以根据网络参数的重要程度，实时分配其对应正则化系数的增量，从而将一些不太重要的参数绝对值逐渐压缩到零。通过这种方式，可以将神经网络的训练和剪枝融合到一起，在训练过程中逐步压缩不重要参数的绝对值，最终去除它们。

相比SPP, 增量正则化方法在AlexNet（ImageNet）上将推理速度提高到原来的4倍,也能够提高0.2%的识别率。在将网络推理速度提高5倍情况下，识别率也仅仅下降了0.8，这相比其他压缩算法也有很大的优势。

增量正则化方法对于三维卷积网络的也有一定的压缩效果，在3D-ResNet18上，将推理速度提高2倍，识别率下降了0.41%；将推理速度提高4倍，识别率下降2.87%。

基于增量正则化方法，我们参与了AVS和IEEE标准的制定，提出的算法成功的写入到国家标准《信息技术 神经网络表示与模型压缩 第1部分 卷积神经网络》中，同时也被写入“IEEE Model Representation, Composition, Distribution and Management”标准中并获得今年的新兴标准技术奖。

最近几年，我们还将深度模型压缩技术应用到图像风格迁移、图像超分辨率等底层视觉任务中。2020年的CVPR论文，我们利用知识蒸馏来压缩风格迁移网络。这里是风格迁移网络的例子，即输入两张图片，一张是内容图片，一张是风格图片。通过风格迁移网络生成一张图片，将内容和风格融合起来。我们需要做的事就是压缩风格迁移网络的大小。

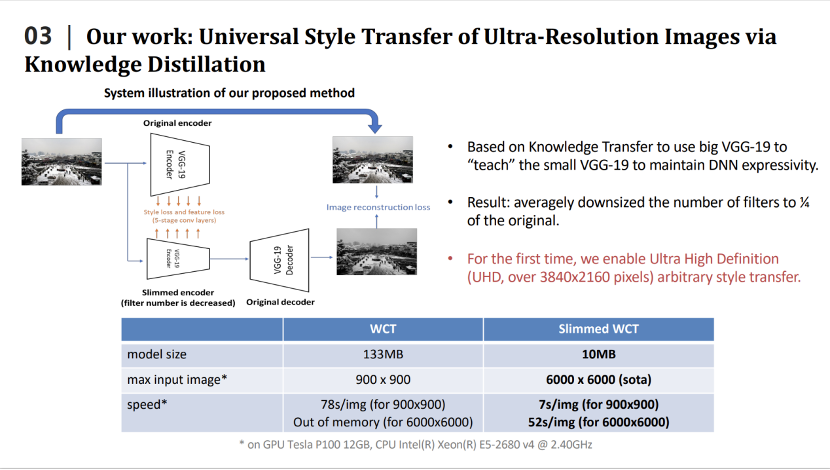
我们利用知识蒸馏来压缩风格迁移网络，即设计小的学生模型，用小的学生模型来模拟大的教师模型的输出，从而达到压缩大的教师模型的目的。我们也设计了针对风格迁移网络的损失函数，更好的完成了知识蒸馏的任务。我们提出的方法有很好的性能，例如在2020年效果比较好的WCT风格迁移网络，整个模型的大小是133m，经过压缩之后只有10m。一块GPU上使用WCT最多可以同时处理900×900的图片，压缩之后，同样的GPU上能够处理6000×6000的图片，在处理速度上，处理900×900的图片，WCT需要花费78秒，压缩之后只需要7秒，同时处理6000×6000的图片，在单卡的GPU也只要花费52秒的时间。

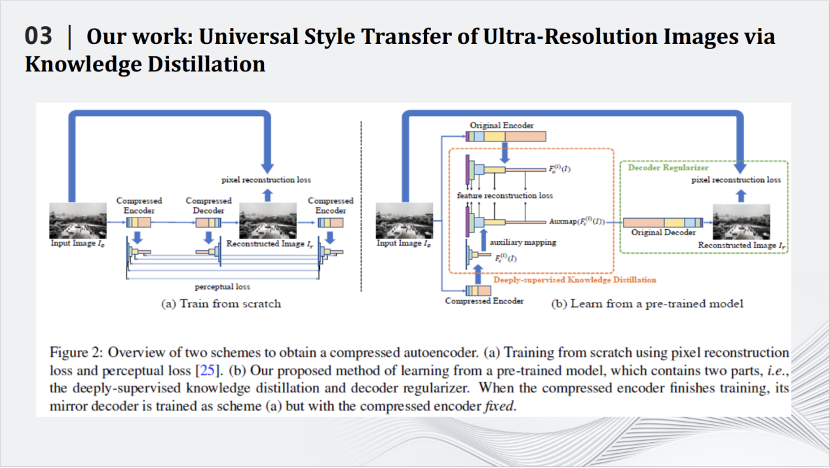
可以看到，通过我们的模型压缩技术，即便是4,000万像素图片的风格迁移，放大后的图像细节依然清晰。

在人脸识别方面，我们也使用了知识蒸馏的方法。这是2019年发表在ICIP的论文，人脸识别中有个三元组的损失，即图片左上角。其中有一个超参数m。这个m是不可以变化的。通过改进，我们将m变成了一个可变的参数，这个参数能够由学生网络计算两个图之间的距离，用距离的方式将m确定下来。基于这种动态的超参数，我们规划了知识蒸馏算法，获得了不错的效果。

我们实现了可能是世界上第一个公开的2M左右的人脸识别模型，同时在LFW数据上达到99%以上的识别率。同时，我们将所做的小型化人脸识别模型嵌入到芯片中，让人脸识别获得了更多的应用。

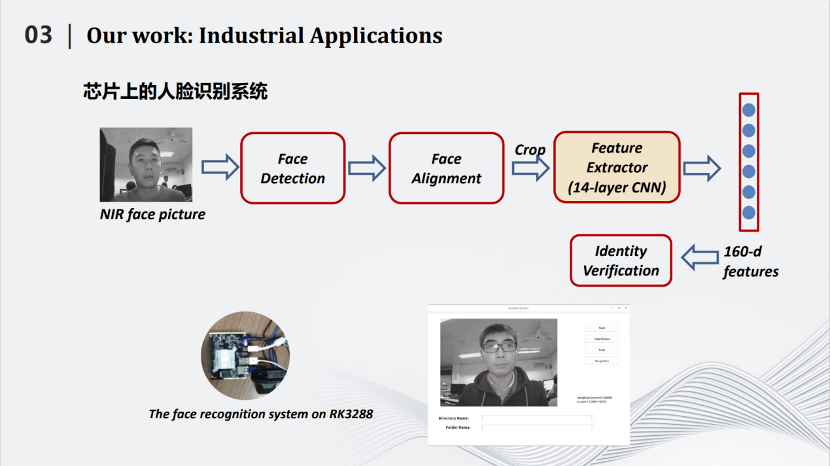
在瑞芯微RK3288上，原有的模型处理一张图片大概在0.31秒。而我们这个压缩后只有2M左右的模型，处理一张图片的时间在0.17秒左右。

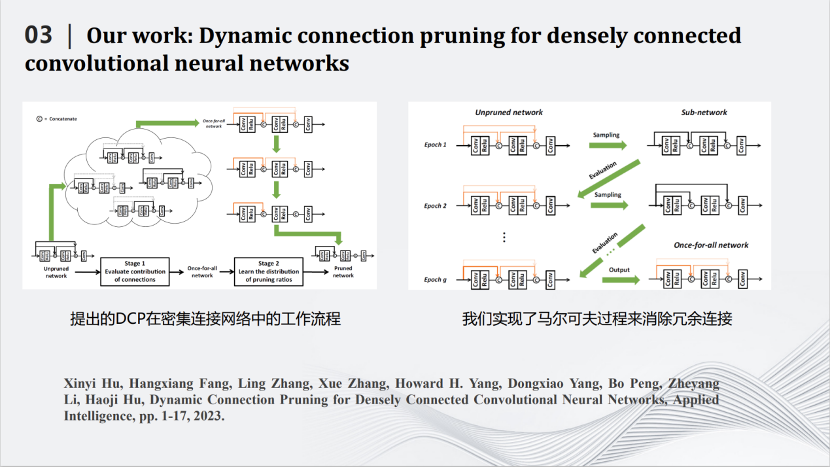
2020年开始，我们和华为合作，将深度压缩模型应用在图像超分辨率上。卷积神经网络是一个先处理局部，再处理全局的模型。而在超分辨率网络中，局部信息很重要，需要用跳线连接前面和后面的层。每一个跳线不仅把数据传送过去，还要同时将那一层的特征图传过去。后面的层不仅仅要处理自己那一层产生的特征图，还要处理前面传送过来的特征图。然而，不是每一个跳线都重要，都需要保留。于是我们规划算法，删除一些不重要的跳线，同时也删除了传送过来的特征图，从而降低了图像超分辨率网络的计算量。我们采用马尔科夫过程建模目标函数，消除冗余的跳线，从而完成对超分辨率网络的压缩。

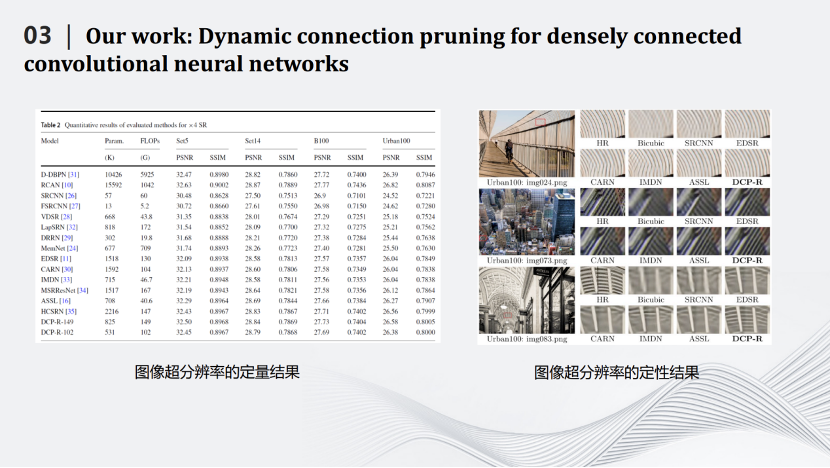
左边表格是一些定量的结果。FLOPs是网络中加法和乘法的次数。经过压缩之后的模型DCP-R-102的FLOPs只有102G，与计算量最大的网络D-DBPN相差50多倍的计算量，而图像的PSNR和SSIM基本不变。右边图片是定性结果，可见，我们的网络DCP-R可以很好的恢复图片的纹理和细节。

这是关于图像超分辨率的另一个工作。这里我们将将蓝色的大网络拆成两块，通过互蒸馏（cross knowledge distillation）这种方式进一步完成对超分辨率网络的压缩。右图是具体的定性和定量的结果。

这篇发表在期刊Pattern Recognition上的文章所做的事情是对深度模型进行量化。最极致的量化叫做二值化（binarization），即对每个参数只用+1和-1两个值来表示。如果每个参数都只是+1和-1，那么网络计算中矩阵的乘法将可以变为加减法，这样就比较适用于类似FPGA这种对于乘法不友好的硬件系统中。但是二值化也会带来一定的坏处，由于每个参数取值范围变小，整个网络的性能会有极大的下降。我们在将网络二值化的同时，为网络加一些辅助的并行结构，这些并行结构是通过网络搜索出来的，也都是一些二值化的分支，即图中红色的部分。加入并行结构后一方面让二值化的性能有了提升，另一方面也让计算增量保持在可控的范围内。利用下方的公式，综合考量精度（accuracy）、特征图相似性（similarity）和复杂度（complexity）三个方面，构造目标函数，在提高精度的前提下尽量减小复杂度，从而达到模型精度和复杂度的平衡。最近我们也在尝试使用重参数化的方式，将这些增加的结构合并到以前的网络当中，从而使网络结构不发生改变的前提下，进一步增加网络二值化的效果。

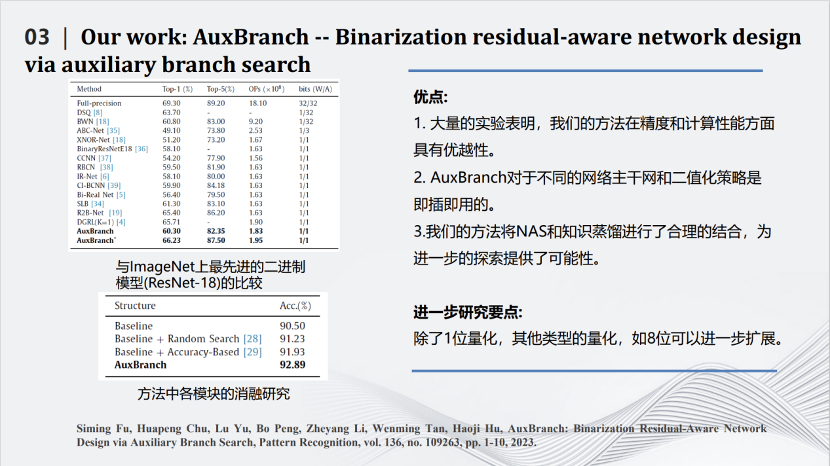
在ResNet-18上可以看到，使用上述方法可以把90.5%的识别准确度变成92.8%，同时计算量没有提升特别多。

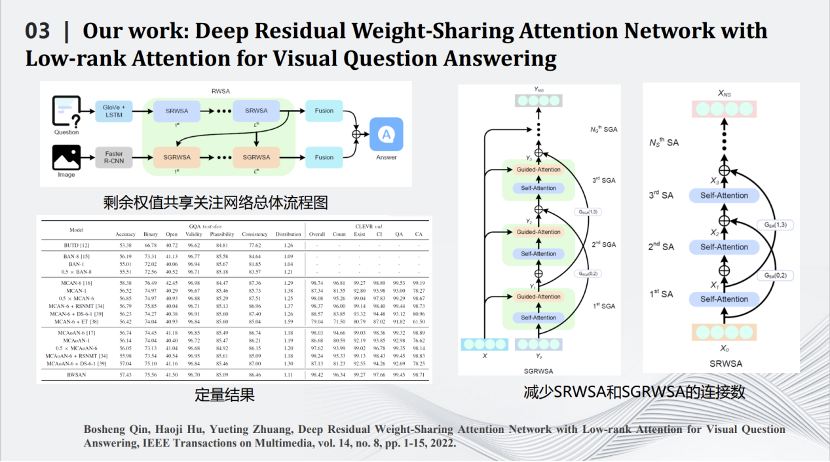
我们也是比较早做Transformer压缩的实验室。Transformer压缩的第一步是用矩阵理论对Transformer中Q、K、V三个矩阵进行分解，用小的矩阵相乘和相加代替大矩阵的相乘。通过一些理论推导，证明在特定场合下相比原有的矩阵计算准确度上界会有一定提升。压缩的第二步是减掉Transformer网络里的跳线。通过这两个相对简单的压缩方式完成对Transformer网络的压缩，同时将其用在智能视觉问答任务中。

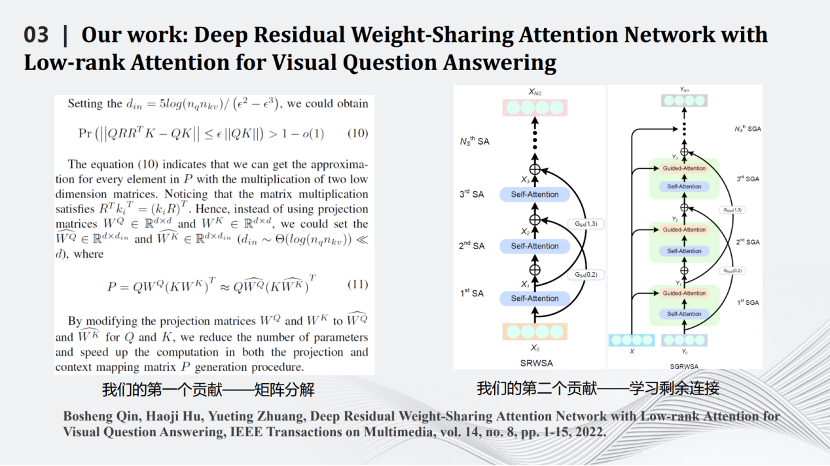
这是一些定量和定性结果的比较，可以看到我们的算法在保留原来性能的同时大幅度减少了网络的计算量。

最后，讲一下我认为这个领域可能有前途的未来发展方向。

首先，利用神经网络压缩技术弥补大规模语言和视觉基础模型的不足是迫在眉睫的方向。大模型消耗过多的计算量和存储量，如何将大模型变小是一个重要的科学问题。一些具体的问题包括，如果大模型是可以做100种任务的通才，那么如何将其转变为只能做1种任务小模型，也就是专才？这里有很多空间，值得继续挖掘。

第二，针对流行的特定任务网络进行压缩，例如Nerf和扩散模型等。但是，如果我们不能在方法上有所创新，只是一昧追逐流行的网络进行压缩，也会陷入内卷的困境。

第三，我认为软硬结合的的网络压缩算法是值得深入研究的方向。将硬件参数和硬件结构作为优化函数的一部分写入到网络压缩算法中，这样压缩出来的网络就能够直接适配到专门的硬件上。

第四，神经网络压缩算法和通信领域的结合。例如增量压缩，即设计神经网络压缩算法，在发送端首先传输网络最重要的部分，接收端首先收到一个识别精度较低的模型；随着更多的传输，接收端能逐步接收到越来越精确的模型。这个想法与图像或视频的压缩类似，可以完成神经网络模型在不同环境和资源下的个性化部署。

最后，我比较关注的是理论方面的研究，我暂且把它称为深度神经网络的信息论。目前的模型压缩算法设计主要靠经验，欠缺理论基础。一个重大的理论问题是，对于特定的任务、数据和网络架构，实现特定的精度所需要的最小计算是多少？这个问题当然是有一个明确的答案，但目前我们离这个答案仍然非常遥远。就像香农的信息论在通信领域的基础地位一样，我们也期待深度神经网络的信息论早日诞生。

我的演讲就到这里，以下是我们实验室的网页、联系方式，以及一些开源的代码，欢迎有兴趣的听众和我们联系。谢谢大家。