解释城市｜为何京沪GDP相关性达99.9%，却没因果关系

人口、产业、经济、社会这些现象都具有明显的空间地理属性，为什么空间上的有些现象很相似，而有些现象差别很大，这些都与空间相关性密不可分。一个城市的犯罪率与失业率有怎样的关联？富裕的城市周边是不是都是富裕的城市？制造业发达城市的周边城市是不是制造业也很发达？北京与上海的经济发展速度有怎样的关联？以上种种问题，我们都可以利用空间相关性的相关理论去加以研究。

一、万物互联，具有普遍意义的一般相关性

马克思主义哲学认为，事物之间具有普遍的联系。这句话用现代统计科学的语言表述就是，任何两个变量之间都可能存在相关性。1884年开始，英国皇家科学院院士弗朗西斯·高尔顿（此人也是进化论提出者达尔文的大表弟）研究人的遗传现象时不断收集有关人的遗传特征数据，他发现，高个子男性的儿子往往身高也比普通人高，矮个子男性的儿子往往身高比一般人矮。不仅如此，父亲与儿子的手臂长度、头部长度等很多体型特征数据都有这样的规律，一开始他把这些具有这种特征的变量认为是遗传的“共同相关”（co-related）。

后来，他的学生卡尔·皮尔逊（Karl Pearson）干脆将其称之为“相关性”（Correlated），并在高尔顿的一些工作的基础上进一步提出了“皮尔逊相关系数”这一变量，用来衡量两个变量之间的相关性强弱。图1 就是不同相关性下两个变量的散点图。相关性系数通常在-1到1之间，-1表示完全的负相关，1表示完全的正相关，0则表示没有相关性。生活中，完全正相关、完全负相关以及完全不相关的例子都不太多，大多数都是一定的相关性，比如管理学中著名的“啤酒与尿布”案例（即很多超市发现购买尿布的父亲也会顺便给自己买一罐啤酒，这两件商品在同一个篮子的可能性较大）的相关性系数大概是0.2，是典型的正相关性。这里顺便提一句，除了皮尔逊相关系数，还有一个“肯德尔相关系数”也比较常用，这个相关系数是由英国统计学家Maurice Kendall在1938年提出，他的想法也很简单，不使用原始的数据来计算相关系数，而是用排名，比如班级里语文成绩第一的学生，如果数学成绩也是第一，语文第二的学生，数学也是第二……那么肯德尔相关系数就是1。并不在乎他们的实际成绩是多少，只需要知道排名就可以了。

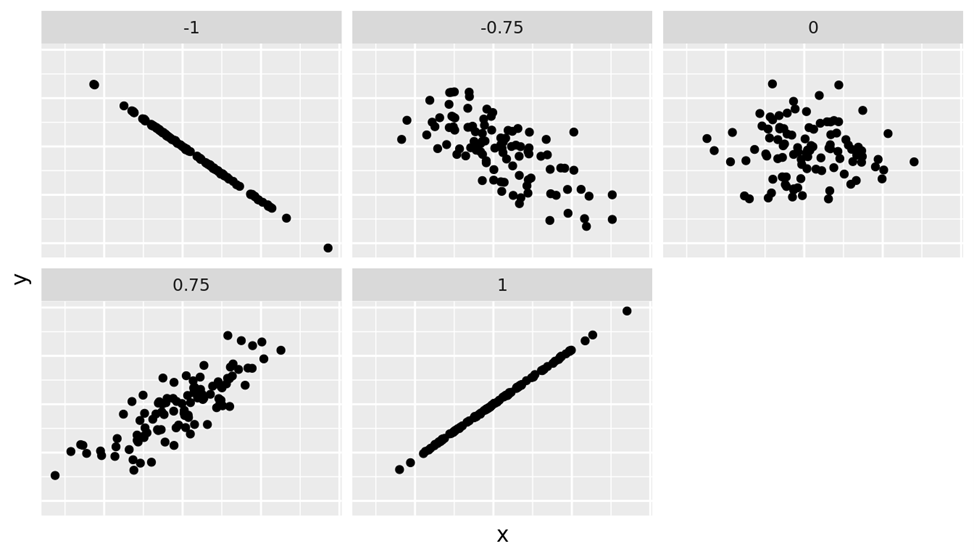
图1  两个变量（X和Y）在不同相关性系数下的散点图。

二、空间相关性：测度城市犯罪率与失业率仅是一种应用

广义上看，只要变量与地理空间相关都能成为空间相关性。比如，有学者研究过城市犯罪率与失业率之间的相关性约为0.6-0.7，因为是采用不同城市的犯罪率与失业率，所以这就属于空间相关性的一种。但这种相关性所嵌入的空间意义并不大，甚至在具体操作时，城市的经纬度、城市间距离，这些表明空间特征的测度对犯罪率与失业率的相关性影响并不大。因此，狭义的空间相关性，人们更加关心一种现象，就是某些经济社会现象有没有在地理空间单元上呈现集聚效应，同一种社会经济现象在不同的空间位置有什么本质性差别和联系。举个例子，富裕的城市周边是不是都是富裕的城市，制造业发达城市的周边城市是不是制造业也很发达？

解决这类问题的历史渊源颇深，1939年9月二战开始时，一个学习统计学和数学出身的22岁澳大利亚小伙子帕特里克·莫兰（Patrick Moran）恰好从剑桥大学研究生毕业，加入了英国国防军事的供应部，负责利用他的数学知识开发火箭结构。但是，令他沮丧的是，军事部门总是以各种保密为理由，不提供给他任何计算的背景和应用实践案例。一气之下，1942年他辞职加入了位于伦敦的澳大利亚科学联络办公室，在那里他时间相对自由，工作之余还加入了英国皇家统计学会，认识了前面提到的英国统计学家肯德尔。受他启发，1950年帕特里克·莫兰在著名杂志《生物统计学》（这本杂志的创刊人就是前文的卡尔·皮尔逊，世界就是这么小！）发了一篇文章《连续随机现象的一些说明》，文章中，他仿照皮尔逊的相关系数提出了空间上的相关系数，不同的地理单元根据他们的相邻情况给出了同一变量的空间相关系数。后人为了纪念他提出的空间相关指数，将全局空间的相关性指数命名为莫兰指数。跟皮尔逊相关系数很相近，莫兰指数为1，表明空间集聚，即富裕的城市周边都是富裕的城市，制造业发达城市的周边城市制造业也很发达。而莫兰指数为-1，表明空间分散，即富裕的城市周边都是欠发达城市，制造业发达城市周边城市制造业都不发达。莫兰指数为0表明无迹可寻，集聚与分散交织在一起。

图2  三种不同的空间相关性，从左到右莫兰指数分别为-1,0和1。

但是莫兰指数只回答了空间上有没有相关性。到底是哪里和哪里相关性较强还不清楚。1995年，亚利桑那州立大学的Anselin L .教授提出了一种局部的莫兰指数，用来寻找究竟哪块区域集中度高，相比1950年莫兰提出的全局莫兰指数，局部莫兰指数就好理解很多。要知道一个区域与周边区域的相关性强弱，只需要知道两对关系，一个是这块区域与它邻居的平均水平谁高谁低，一个是它邻居与整个区域的平均水平谁高谁低，如果两个同高同低，就是正相关，否则负相关。并根据这两对关系将空间相关性划分为四种情况。比如图3，假设表示的是不同区域上的人口密度，方格的密度颜色越深表示密度越高，中心的方格是我们的研究区域。现在要看这个研究区域是不是与周边和全域有相关性，存在四种情况，分别是高高集聚区、低高集聚区、低低集聚区和高低集聚区，以高高集聚区为例，研究的这个区域（可以是一个城市，也可以是一个县）的人口密度比周边城市都要高，而周边城市的人口平均密度又比全国人口平均密度高，那么我们研究的这个区域就是人口密度的高高集聚区，区域集聚特征就比较明显。 

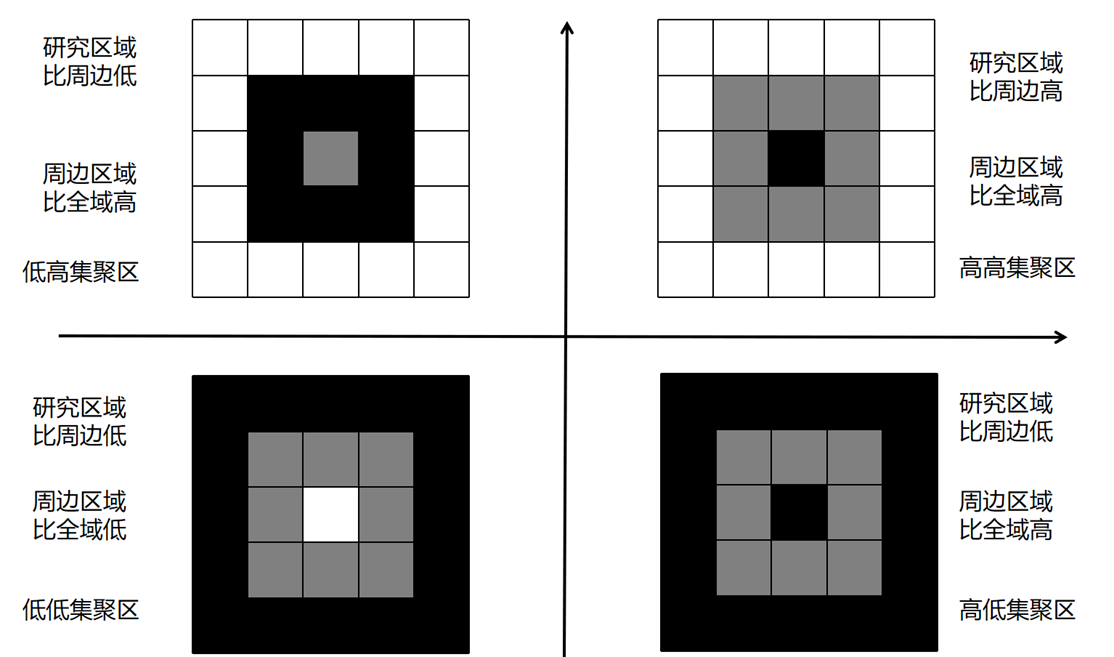
图3 局部莫兰指数的四种情况（颜色越深，变量值越大）。

三、为何京沪GDP有相关性，而非因果性

最后需要指出的是，无论是一般的相关性还是空间的相关性，都是表明空间上的两种现象有关系以及这种关系的相对强弱，并不代表因果性。其实这个很好理解，举个例子，北京市GDP从2003年的2257.8亿元增长到2022年的41610.9亿元，同期，上海GDP也从2680.4亿元增长到44652.8亿元，从这20年的两者序列看，相关性达99.9%。但是却不能说两个城市之间的经济发展存在因果关系，不是由于一个城市经济增长，另外一个城市经济才增长的。因此，空间相关性更多表达的是一种空间上同时发生的现象或者趋势。而空间因果推断最近几年发展迅速，关键在于需要找到一些影响因子，但空间相关性无疑为此奠定了重要基础。

-----

“解释城市”专栏由上海发展战略研究所戴跃华博士主持，关注城市科学发展的前沿趋势，解释城市科学以及城市中人类行为动力学的一般特征和规律，探究利用前沿城市科学理论优化城市治理的路径和方法。