- +1
什么是涌现?人工智能给你答案
原创 张江、袁冰 集智俱乐部
导语
涌现是复杂系统诸多现象中最神秘莫测的一个:从鸟群聚集、蚂蚁觅食,到生命游戏、大模型涌现能力,再到宇宙起源、生命演化、意识产生,都可以看作是涌现。那么,究竟什么是涌现?涌现可以分成几种类型?涌现和因果是什么关系?我们应该如何定量刻画涌现?又应该如何在数据中自动检测出涌现?
在因果涌现第三季读书会第一期,北京师范大学系统科学学院教授张江老师,和集智科学研究中心技术与产品顾问袁冰老师进行了主题为“涌现、因果与人工智能”的分享,系统梳理了涌现、因果、因果涌现、涌现的分类、因果涌现的识别,及其与隐空间机器学习、世界模型等人工智能算法之间的关系。本文由北京师范大学系统科学学院研究生杨明哲整理。
研究领域:因果涌现,涌现分类,有效信息,人工智能,G-emergence,神经信息压缩器
张江、袁冰 | 讲者
杨明哲 | 整理
梁金 | 编辑
目录
1. 涌现、分类与因果
2. 因果涌现与有效信息
3. 因果涌现识别与人工智能
4. 读书会整体框架
一、涌现、分类与因果
1. 涌现现象
如果你曾经观察过蚂蚁,你会惊讶地发现,当它们聚集成蚁群时,会展现出一种不可思议的“智能”表现。例如,它们能够自动发现从蚁群到达食物的最短路径。这种智能表现并不是由于某些个体蚂蚁的聪明才智,因为每只蚂蚁都非常小,不可能规划比它们身长长至少几十倍以上的路径。这种行为是由于许多蚂蚁聚集成一个蚁群,才表现出来的智能。我们把这种现象称为涌现(Emergence)。
什么是涌现?当我们用这个词来描述蚁群这样的现象时,是想描述它所体现的整体大于部分之和。为给出一个更加规范的定义,我们说蚁群这样的整体是一个系统,而其中每个蚂蚁便是构成这个系统的基本元素。于是我们可以给出涌现的定义:如果一个系统的属性不是其任何基本元素的属性,那么它就是涌现的。事实上不只是蚂蚁,从鸟群的灵活有序,到大脑产生意识,皆是涌现出来的特质。接下来介绍几个其它的涌现案例让读者更多体会涌现这个概念。

图1.许多小鱼聚在一起拥有了大鱼一般的威慑力,这是单独一只小鱼所不能拥有的
生命游戏
1970年,英国数学家约翰·何顿·康威(John Horton Conway)发明了元胞自动机。这是一种无限的、二维正方形的栅格单元网格,每一个单元格有2种状态可能性:活或死的(或者黑和白)。每个单元格都与其八个相邻的单元交互。把每个单元格看作一个细胞,该系统具有以下规则:
1. 任何有两个或三个活邻居的活细胞都可以存活。
2. 具有三个活邻居的任何死细胞都将成为活细胞。
3. 所有其他活细胞将在下一代死亡。同样,所有其他死细胞仍保持死亡状态。
这便是大名鼎鼎的生命游戏,至今已作为一个经典的复杂系统被众多学者研究。它吸引大家研究的点在于,作为基本元素的细胞有着非常简单的交互规则,但当我们把视点放在全局,却会发现很多有意思的图案(pattern)。有些是静态的,像图3中的“方块”、“面包”等等,随着时间不再变化。还有一些则是周期振荡的,甚至像水面上的波一样向某一个方向传播。比如说“滑翔机”,是一个朝某一方向“运动”的周期动态图案,用它构造布尔电路,甚至可以在生命游戏里搭建抽象的计算机,支持通用计算。

图2.生命游戏在某一个时间步上的全局状态
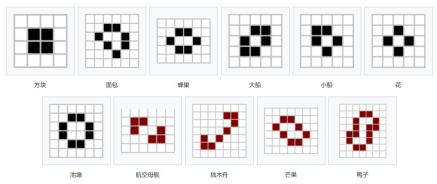
图3.生命游戏里的部分静态案例
阿米巴虫的例子
生命游戏的例子体现出,我们在计算机上就可以通过简单的编程,来复现一个复杂系统的涌现现象。接下来介绍的阿米巴虫的例子,则让我们认识到人类甚至可以向生物界中的涌现现象学习,为人类工程师的设计提供借鉴。
阿米巴虫有两种生存状态,一种是作为大型黏菌存活,而当它饥饿时,会分解出很多微小的单细胞生物去觅食。如果它们发现了一个食物点,就会构建一条管道输送食物给黏菌。我们会发现,这些管道构建成的运输网会被不断优化,一些低效的管道会渐渐消失,而对于留下来的运输网,如果去测量它的运输效率等指标,则会发现它几乎就是最优的设计。这启发科学家借鉴阿米巴虫的生长来设计城市的交通运输网。如图4所示,实验中特意摆放食物点使之与城市的各个地点坐标相似,便可以得到阿米巴虫“设计”的交通运输网了。

图4.阿米巴虫自发演化出的食物运输管道
蚁群觅食的例子
以上举出的涌现现象何以可能?我们再来分析一下蚂蚁觅食的案例。科学家进一步发现,蚁群发现觅食最短路径包含了以下三点:1. 蚂蚁找到食物就会释放信息素;2.信息素会吸引更多的蚂蚁来聚集,同时信息素也会挥发;3.蚂蚁和信息素形成正反馈回路,把路径长短上的细小差异放大,从而筛选出最短路径。借此我们大致可以定性地描述涌现发生的机制:局部作用产生正反馈机制,从而导致宏观上“令人惊异”的现象。这里面不需要一个上帝一般的角色来做全局的考虑和设计。
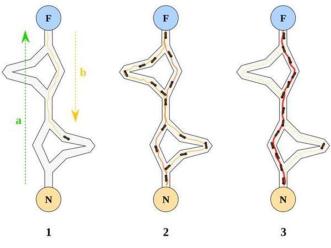
图5.蚂蚁自动发现觅食最短路径
大语言模型的涌现能力
涌现这个概念近年来越来越火,尤其是ChatGPT的流行,让更多人关注大语言模型(LLM)与它的涌现能力。这里的涌现更多是指,随着模型规模变大,突然在某一刻拥有了以前没有的能力,比如能在自然语言交互中回答一些智力题。这种神奇的进步在直觉上和前面所说的自然界中的涌现现象似乎一样,但实际是有差异的,因为这里没有局部正反馈反映到宏观全局的过程,其背后原因更多和思维链(chain of thoughts)有关,这里不过多解释,可参考之前的文章。但这不妨碍我们进一步挖掘其背后的秘密,在以后看到更精彩的大模型涌现。
大模型还体现出另一种令人惊讶的特性,即随着尺度的变化,计算准确度呈现幂律上升,这就是规模法则(scaling law)。规模法则在各种不同的复杂系统中都会出现,从生物界到城市科学。比如在鸟群中,鸟和鸟之间的关联便是关于距离的幂律函数。这其实也是一种涌现出来的现象,是一种统计上的涌现现象。它的出现意味着我们抛弃了大量无关信息,抓住了一些关键指标的变化。以它为切入口,我们可以深挖其背后的机理,从而帮助理解前面举出的那些难以规范描述的涌现现象。
2. 因果与涌现
为了理解涌现现象,我们发现可以从因果的视角入手,来重新阐释复杂系统里个体与整体的关系。回到蚁群的例子,试想一个蚁群过河的场景。为了让整个蚁群能安然渡河,与水面接触的那几只蚂蚁便成了牺牲品。这里便存在一个因果关系,而且与我们更为熟悉的因果方向不同。我们更容易接受的是,因为蚂蚁作为个体的某些行为,所以有了蚁群在宏观上的某些现象,这在亚里士多德的四因说里是质料因。但在蚁群过河的例子中,因为蚁群要在水面上生存,所以牺牲了边缘的几只蚂蚁,出现了自上而下的形式因。这时候我们或许更倾向于把整个蚁群看作一个超级生命体,而不再是一只只蚂蚁的排列。

图6. 一个蚁群在水面上,体现出向下因果
类似的例子还有很多,都涉及到因果律的变化。有的复杂系统里自上而下的因果相比于自下而上的因果体现的更明显,还有的系统中只能在宏观层面去解释一些结果,而不能用微观的个体去做因果上的解释。
那因果和涌现到底是什么关系?Jochen Fromm 在中指出,对于所有的结果(effect),我们都会试图找到它的原因(cause),但涌现现象是我们在宏观上观察到一个现象却无法简单归因的。这样的洞见让我们认识到,对因果的研究是理解涌现的一个途径。于是我们有了因果涌现(causal emergence)这样一个概念和研究课题。我们希望借此能对涌现有一般性的研究,而不只是在一个个具体的案例里讨论涌现现象。
3. 涌现的种类
我们接下来来看对于涌现这个概念,历史上已经有了哪些定性的研究。首先介绍Jochen Fromm 对涌现的分类。如图7,图中箭头表示因果关系,那么根据因果关系的不同,可以把涌现分为四类。
首先是简单涌现,只有自下而上的因果关系,比如对一些变量求均值,这种普通的统计特征我们非常熟悉了,不是我们关注的重点。有意思的事情发生在自上而下的因果关系的出现,这时便是弱涌现,像前面介绍过的蚂蚁觅食就是这一类。生命游戏则属于多重涌现,在一次生命游戏中可以同时观察到或静态或动态,大小不同长相不一的图案涌现出来。强涌现则是考虑了不只两个尺度,同时有微观、介观、宏观三个尺度,而介观的存在完全隔离了微观与宏观之间的因果关系。例如从细胞到多细胞生命体再到智能与意识的存在。
Fromm, Jochen. "Types and forms of emergence." arXiv preprint nlin/0506028 (2005).

图7. Jochen Fromm 对涌现的分类
需要说明的是,有些涌现离不开主观视角的介入。有些涌现是客观固有的性质,比如蚂蚁觅食,可以用客观指标来度量蚁群觅食的能力,这样的涌现可以被称作本体论的涌现。还有些涌现现象则源自观察者的简化,比如我们观察云彩的时候,会认出某些云朵形状类似我们熟知的人脸。这样的宏观现象一样无法归因于每个运动的水蒸气分子,但它是客观物质与人类认识共同形成的。这种涌现可以被称作认识论的涌现。两种涌现都很重要,都是我们要研究的对象。
另一位哲学家 Mark Bedau 也提出了自己对涌现的分类,和 Jochen Fromm 的理论也有联系。Fromm 所说的简单涌现,便是Bedau提出的名义的涌现。而 Fromm 的弱涌现与多重涌现合在一起则是 Bedau 认为的弱涌现。两个人的共识在于对强涌现的认识和界定。强涌现确实是最神秘也最令人着迷的一种。相比于 Fromm 的理论,Bedau 的分类更加简洁。

图8. Bedau 涌现理论的文章
Bedau, M. Downward causation and the autonomy of weak emergence. Principia: an international journal of epistemology 2002, 6, 5–50.
除了哲学上的探讨,Bedau 更大的贡献在于,用格兰杰因果检验这样一个量化手段解释了什么是弱涌现,此时弱涌现也可以叫做 G-emergence。如图中A、B两个时间序列,我们回归分析变量An,可以得到A自身的历史信息An-1与B的历史信息Bn-1对它的解释。如果仅凭借A自身的历史信息就可以解释An,便定义A是G自主(G-autonomous)的。那什么是弱涌现呢?在一个鸟群模型的例子中,每只鸟的运动便是微观上的时间序列,而整个鸟群质心的运动定义为宏观上的时间序列。如果宏观时间序列是G自主的,而微观时间序列不是,还需要依靠宏观质心运动的历史信息来预测下一时刻的微观状态,那么便定义这个系统是弱涌现的。该定义讨论了自上而下的因果关系,而且是以机器作为观察者视角,用算法发现了模型原本不包含的向下因果,属于我们之前所讨论的认识论的涌现。
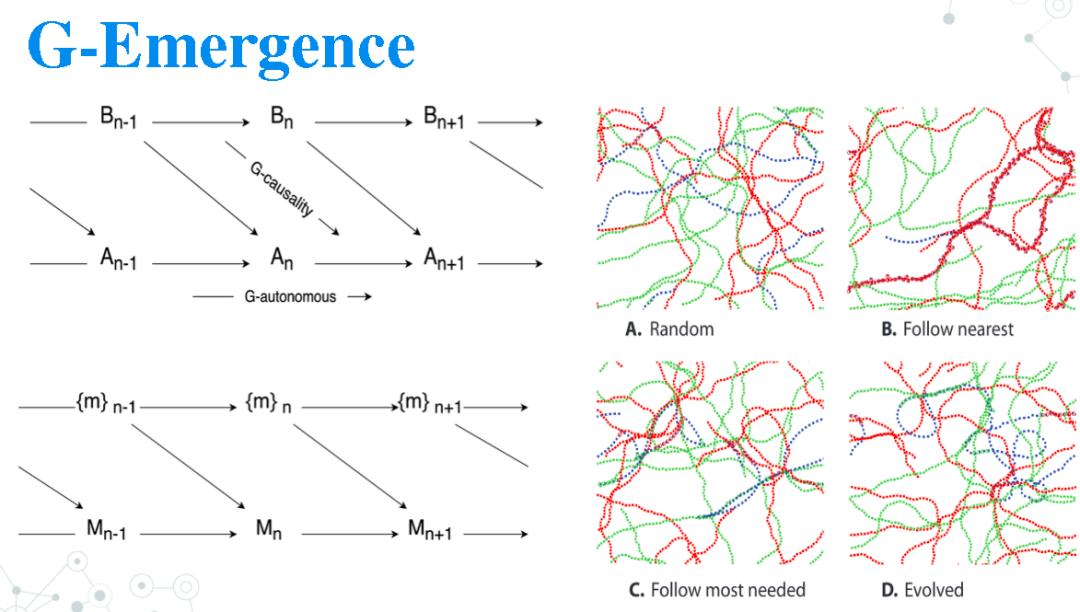
图9.Bedau对于弱涌现定量的定义
二、因果涌现与有效信息
对于复杂系统的因果涌现,除了以上讨论的定性研究,我们更希望能搭建一个量化的理论框架。Erik Hoel 作为因果涌现理论的正式提出者,最大的贡献便是以因果为工具对涌现现象进行了定量的刻画。
Hoel, E.P.; Albantakis, L.; Tononi, G. Quantifying causal emergence shows that macro can beat micro. Proceedings of the National Academy of Sciences 2013, 110, 19790–19795.
如图10所示,横轴表示系统动力学演化时间,纵轴则是同一系统的不同尺度。我们常常能观测到微观尺度上,系统在某一动力学规则下演化,比如在一个密闭空间里,大量气体分子在牛顿定律下运动。但这样的运动非常无序,很难研究清楚,也就是说微观动力学f的因果效应强度会比较弱。为解决这一问题,我们经常会使用某一种粗粒化手段,把系统的微观状态映射到某一宏观尺度上。比如对于刚才提及的气体系统,我们开发出温度、压强、熵等一系列宏观指标,那么所有气体分子的速度和位置等变量就与这些宏观指标建立起了映射关系。在这个宏观尺度上,我们往往会发现更加简洁的规律,比如有理想气体方程PV=nRT。这时候可以说该宏观动力学F的因果效应强度高。如果有宏观动力学的因果效应大于微观动力学因果效应,便认为该系统发生因果涌现。
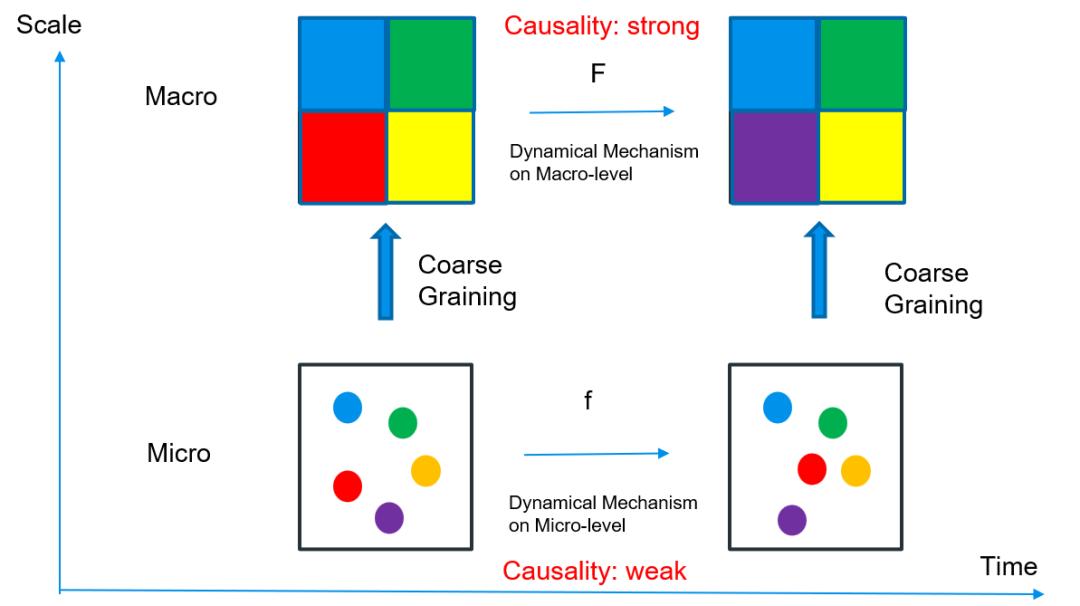
图10.Erik Hoel的因果涌现理论框架
这里的因果效应强度要怎么度量呢?我们接下来介绍因果效应度量的指标有效信息(effective information, EI)。这个概念最早来自 Hoel 的导师 Tononi 的一篇文章,是指对于一个马尔可夫系统,测量输入和输出的互信息,其中输入服从最大熵分布。
Giulio Tononi, Olaf Sporns. Measuring information integration. BMC Neurosci, 2003, 4(31)
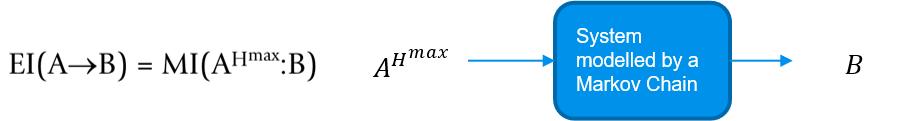
图11.定义有效信息的示意图
Hoel 进一步发展这个概念,同样是在离散的马尔可夫系统中讨论,对于一个转移概率矩阵,可以测量它的 EI。EI 本质是互信息,但仅仅是互信息还不行,因为互信息测量的是关联关系,无法去除数据分布本身带来的混杂影响。为了让互信息能正确衡量系统自身的性质,需要约束输入变量的分布,即人为对输入一端的变量做干预,设定输入变量为均匀分布(在离散系统中等同于最大熵分布),然后测量此时输入和输出之间的互信息,得到的便是 EI。干预这个概念来自 Judea Pearl 的因果理论,正是因为引入了干预这样的手段,EI 度量的便是因果效应强度,是一个动力学内在的性质,与外界数据无关。
值得分析的是,有效信息本身可以被拆成确定性(Det)和简并性(Deg)两部分。确定性度量的是以过去状态预测未来状态的随机性大小,简并性度量的是从未来状态追溯过去状态的随机性大小。在数学上,对EI除以log2(n)做归一化,得到Eff,于是推导可得 Eff=Det-Deg。这启发我们,所谓因果效应强,可以归于两个方面,高确定性和低简并性。图12中提供了几个案例,包括转移概率矩阵和对应的各指标的计算值,供读者参考体会。
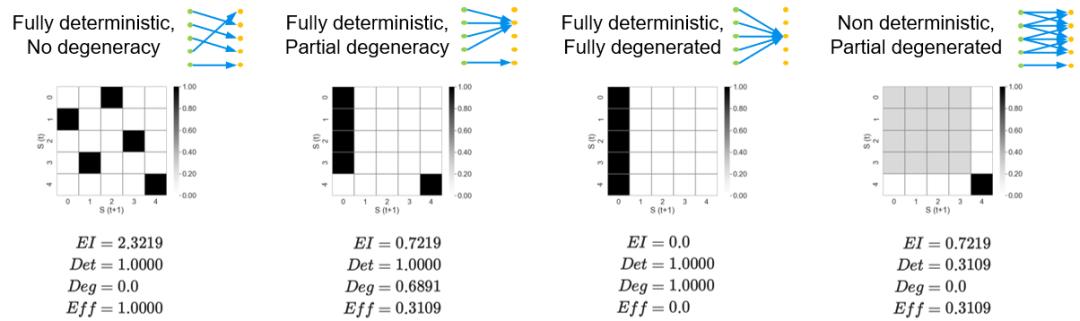
图12.有效信息及确定性简并性计算的案例,其中色块深浅表示转移概率矩阵上每个条件概率的大小
因此,我们可以来回答为什么一些粗粒化策略可以提高有效信息。当输入是某一状态时,输出会有多种可能,是一个具有随机性的分布,如果我们通过粗粒化把这些可能的输出打包为一个输出,就减少了随机性,于是提高了确定性;同理,从某一个输出结果往回追溯,它也会对应多个可能的输入,如果打包这些输入,就能减少这个过程的简并性。这两条路径都可以提高有效信息。
三、因果涌现识别与人工智能
到目前为止,我们已在离散的马尔可夫系统上充分讨论了如何定量刻画粗粒化以及因果涌现,但这本身还是非常理想化的。除了马尔可夫性的假设以外,更重要的是我们已知其背后的动力学,而这在真实世界中几乎不可能,尤其面对复杂系统的时候。所以当我们已收集好微观数据,比如一个多主体系统中每个主体的运动轨迹,需要回答如何从中识别因果涌现的问题。考虑识别因果涌现的时候,需要有粗粒化策略来建立多尺度视角,所以进一步又有两个更加具体的问题:如何在数据中自动得到合适的粗粒化策略以及找到对应的宏观动力学。
到目前,已经有学者沿着这条轨迹做出了成果。这里主要向读者介绍神经信息压缩器(Neural Information Squeezer,NIS)的工作,其它相关工作会在后面的读书会中进一步展开。
Zhang, J.; Liu, K. Neural information squeezer for causal emergence. Entropy 2022, 25, 26.
如今,面对大量数据,机器学习是一个主要的处理手段,而NIS便是把机器学习中的神经网络技术借鉴到了因果涌现识别的问题中来。熟悉神经网络的读者知道,神经网络是一个计算能力强的黑箱,能拟合任意复杂的函数,但同时可解释性很差。这使得它虽然对于普通的预测或分类任务表现不错,可一旦环境变化,它就容易失败,因为它很多时候并没有把握住一个动力系统背后本质的规律。如果我们能用一个神经网络框架学习到因果性更强的宏观动力学,那么这样的神经网络会比一般的神经网络具有更强的可解释性和泛化能力。
具体怎么做呢?回到我们得到的微观数据上,它们通常是多维的时间序列数据,可以假定背后有微观动力学生成这些数据。接下来我们用编码器来对这些数据做粗粒化,得到宏观的数据,其中输出的宏观数据比输入的微观数据维度会更少。对于这些宏观数据,我们用一个神经网络拟合它背后的宏观动力学(macro dynamics)。得到了宏观动力学,我们可以测量它的EI(这里需要先对EI进行拓展,使其可以度量神经网络的因果性。这样的拓展是合理的,因为输入输出只相差一个时间步,神经网络学习的动力学具有马尔可夫性。具体细节见参考文献)。这个EI便是我们要最大化的目标,通过梯度反传来优化编码器和宏观动力学神经网络。
这样似乎就已经解决了前面提出来的问题,找到了因果涌现最强的宏观动力学。但在实操中我们会遭遇平凡解的问题。由前面的分析我们知道,因果涌现来自于高确定性和低简并性。对于机器而言,它总能找到一个特定的高确定同时低简并的策略来满足优化目标,那便是把所有微观数据粗粒化为一个常数值,然后拟合宏观动力学为恒等映射。这种策略得到的宏观动力学EI非常大,但这显然是我们不想要的平凡解。那问题出在哪了呢?
相信读者很快意识到,此时学习到的宏观动力学和微观数据实际没有任何关系,换句话说,它不包含微观的信息。这让我们意识到,一味追求EI这个指标是不行的,需要增加约束让学习的宏观动力学包含微观的信息。NIS的做法是让宏观动力学得到的预测输出再解码回微观,得到对微观的预测。如果这个预测足够准确,那么宏观动力学一定不是平凡解,而会包含微观态的信息。完整的NIS框架如下图所示。
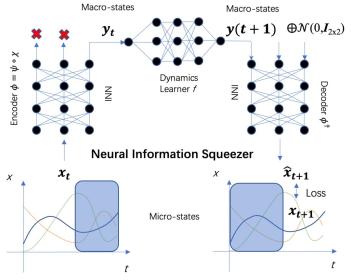
图13. NIS的框架图
首先介绍一下编码器和解码器。编码器所拟合的粗粒化映射分为两部分,首先是一个可逆的神经网络(INN),可以模拟任意复杂的可逆映射,在这个过程中没有任何信息的损失,其次是抛弃维度的操作,相当于一次投影操作,也就是在这一步发生信息的损失。投影保留的分量便是宏观动力学学习器的输入。在另一端解码时,拼接一个标准正态分布的噪音扩充维度,再输入到INN中。编码和解码所用INN共享参数。
我们约束该框架,使微观上预测输出的误差收敛到一定范围内,在这个条件下最大化拟合的宏观动力学。于是整个NIS构建起了一个信息瓶颈,如图14所示,有用的信息在保留的维度里,通过宏观动力学F传递,而经过对INN的训练,投影抛弃的维度自然就是无用的噪音。如此把握系统本质的规律,可以使模型在变化的环境里也可以保证预测的准确和有效性。当然,维度不能保留的太少,否则“通道”太窄,没办法把所有有用的信息传递过去。于是存在某一个宏观维度大小,刚好使对预测有用的信息都传递,而留存的噪音达到最小。这便是瓶颈的含义。这种性质可以在信息指标上体现出来,如果NIS被充分训练,我们可以观察到此时宏观动力学输入和输出的互信息约等于微观态t时刻与t+1时刻之间的互信息。
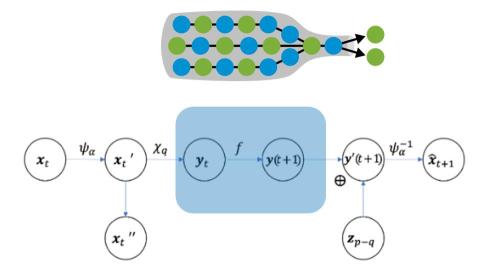
图14.信息瓶颈示意图和NIS因果图
目前NIS已在一些实验上体现出它的效果。下面介绍其中两个实验,其它更多实验细节可见参考文献。首先,为了证明该框架的有效性,我们用简单的弹簧振子模型来做一个数值实验。该模型本身只有两个维度,速度(v)和位置(z)。把这两个维度作为宏观态,在它们基础上分别加减一个正态分布噪音扩充至四维,模拟的是观测噪音。得到的四维变量作为微观数据,使用NIS进行因果涌现识别任务。如图15右图所示,通过遍历各个宏观维度,计算各层EI以及宏微观EI的差值 (CE),果然发现在二维层面上CE值最高,和我们预想的答案一致。同时左图体现出,NIS学习得到的宏观轨迹和真实的宏观轨迹在相空间上非常相似。这说明NIS真正把握到了该系统背后的宏观规律。
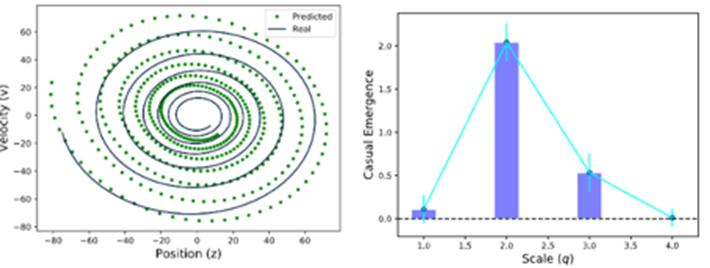
图15. 弹簧振子模型部分实验结果
除了人为构造的简单模型,还要在经典的复杂系统上检验NIS。前面提及的生命游戏便是这样一个复杂系统。那NIS能不能捕捉到人眼很容易分辨出的有趣的图案呢?图16展示的就是以“滑翔机”作为实验对象,此时NIS捕捉的宏观态以及和真实数据的对比。可以看出,训练好的NIS可以在宏观上以分块的形式捕捉到两个滑翔机,就好似人脑识别出滑翔机图案时,对它们进行的抽象。可以期待以后类似的多尺度建模方法可以捕捉到生命游戏更多样的宏观图案。
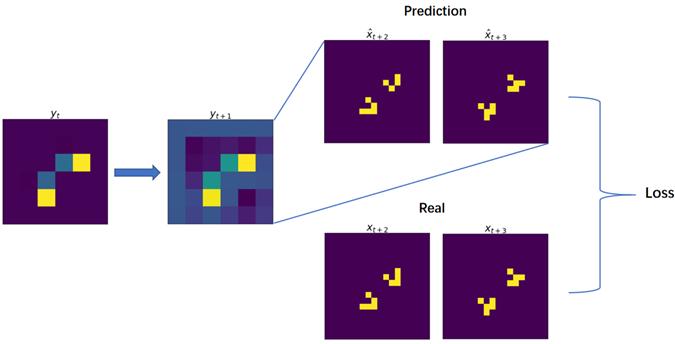
图16.生命游戏部分实验结果
四、读书会整体框架
到这里我们可以做一个总结。因果涌现理论的诞生,是为了以因果的概念来尝试定量刻画原本神秘的涌现现象。当我们能够度量每个动力学的因果性强弱后,如果有宏观的因果强于微观上的因果,便定义因果涌现的发生。而面对现实世界中各种复杂系统,我们需要有自动建模方法能从数据中识别因果涌现,NIS是一个在这方面取得一些成效的工作。
为更深理解因果涌现这一领域,第三季读书会展开了更丰富的问题和理论,比如考虑连续系统上的因果涌现,回顾和因果涌现领域关系密切的经典文献,比如计算力学、协同学、隐空间动力学以及涌现探测等等。其余话题,包括信息分解等,将在第四季读书会更进一步地聚焦和展开。
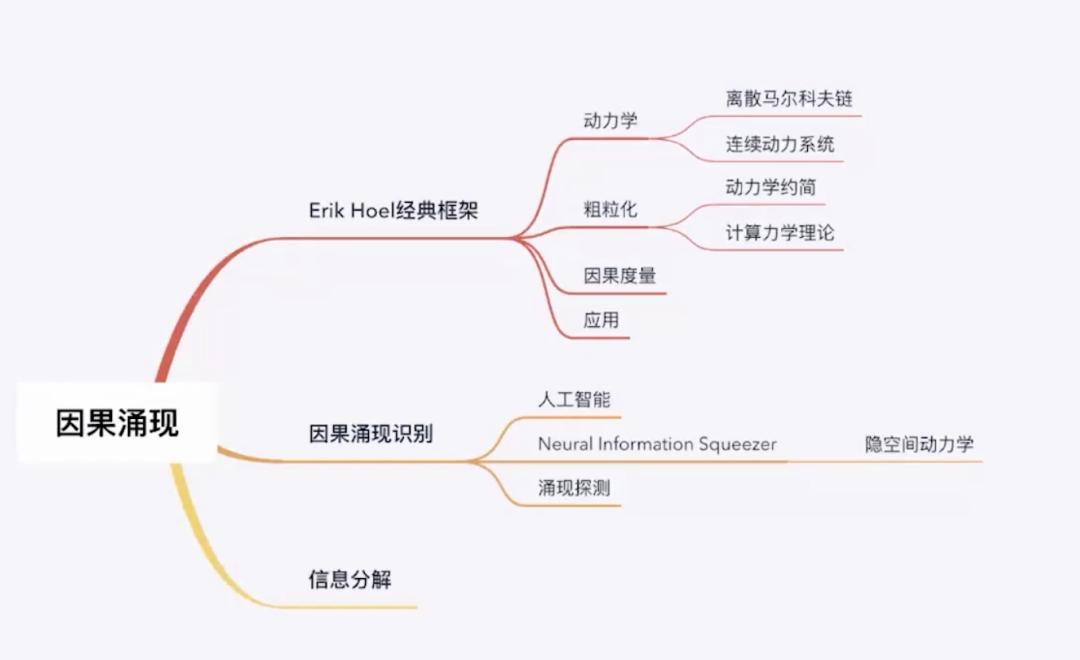
图17. 因果涌现框架图
学者简介
张江,北京师范大学系统科学学院教授,集智俱乐部、集智学园、集智科学研究中心的创始人,曾任腾讯研究院、华为战略研究院等特聘顾问。主要研究领域包括复杂系统分析与建模、规模理论等。
集智斑图个人主页:https://pattern.swarma.org/user/9
袁冰,集智科学研究中心技术与产品顾问。毕业于华中科技大学,研究兴趣包括因果推断、复杂科学,以及人工智能相关领域。集智斑图个人主页:https://pattern.swarma.org/user/46173
因果涌现读书会
跨尺度、跨层次的涌现是复杂系统研究的关键问题,生命起源和意识起源这两座仰之弥高的大山是其代表。而因果涌现理论、机器学习重整化技术、信息论或信息分解等近年来新兴的理论与工具,有望破解复杂系统的涌现规律。而新兴的因果表征学习、量子因果等领域也将为因果涌现研究注入新鲜血液。
原标题:《什么是涌现?人工智能给你答案》
本文为澎湃号作者或机构在澎湃新闻上传并发布,仅代表该作者或机构观点,不代表澎湃新闻的观点或立场,澎湃新闻仅提供信息发布平台。申请澎湃号请用电脑访问http://renzheng.thepaper.cn。





- 报料热线: 021-962866
- 报料邮箱: news@thepaper.cn
互联网新闻信息服务许可证:31120170006
增值电信业务经营许可证:沪B2-2017116
© 2014-2025 上海东方报业有限公司




