光学精密工程·封面 | 基于拓扑优化的电渗流微混合器电极

▍导读

近年来，由于在生物医疗、环境检测、化学分析等领域的广阔应用前景，微流控芯片已成为快速发展的高新技术。其中，微混合器是微流控技术的主要功能器件，为满足不同浓度溶液快速、完全混合的设计需求，微流体的驱动技术是目前的研究热点。

电渗驱动具有驱动系统结构简单、操作便捷且无脉动等优势。现有研究电渗流动微混合器大多是通过改变微混合器的结构、电极排布方式、电压等参数提高样品的混合效率，缺乏对电渗流微混合器电极版图的结构设计工作。目前，电渗流电极版图大多基于尺寸优化和形状优化的方法进行设计，难以大幅提升微流控器件性能。

针对上述问题，中国科学院长春光学精密机械与物理研究所邓永波课题组做了长期的研究工作。2018年，课题组针对电渗流电极版图设计问题发展了拓扑优化方法[1]，该方法使材质插值可以在Dirichlet和Newman边界条件之间进行，这是将拓扑优化应用在控制本体性能的关键一步。课题组也将该方法进一步推广，通过拓扑优化进行微泵设计以获得更大的净流量[2]。

近期，针对上述问题的研究又有了新的进展，该课题组孙建文等在《光学 精密工程》（EI、Scopus，中文核心期刊，《仪器仪表领域高质量科技期刊分级目录》和《光学和光学工程领域高质量科技期刊分级目录》“T1级”期刊）上发表了题为“基于拓扑优化的电渗流微混合器电极”的封面文章。

《光学 精密工程》2023年第17期封面

▍微混合器模型建立

图1为电渗微混合器示意图，作者引入Helmholtz-Smoluchowsk条件将双电子层进行近似约束处理，通过将模型边界条件设置成电势与电绝缘的插值形式，将电渗流微混合器电极设计转化成求解插值材质分布问题。

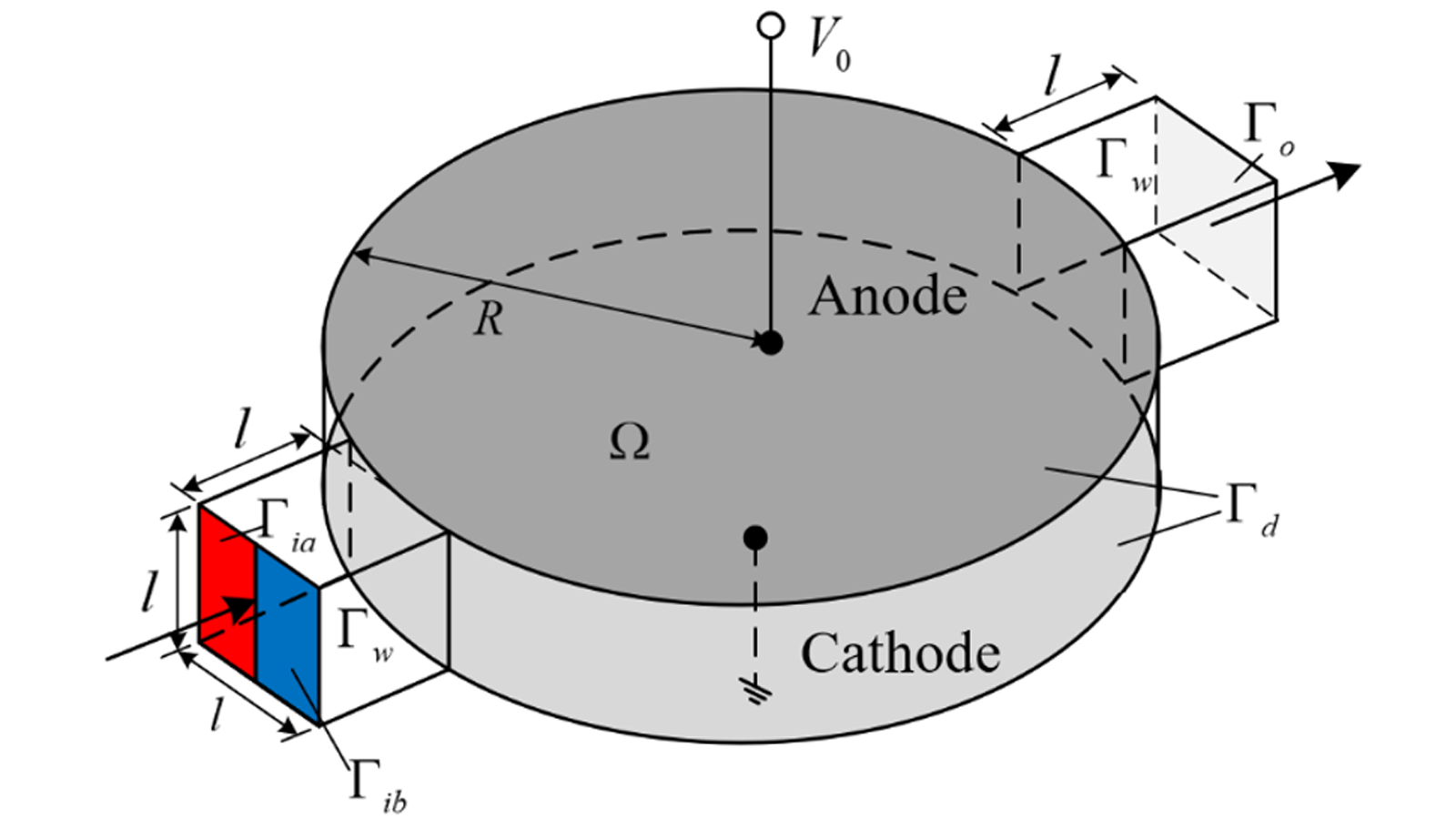
图1：电渗微混合器示意图

▍电渗流微混合器混合效果分析

为验证拓扑优化方法设计电渗流微混合器电极的可行性，我们对微混合器的混合效果进行分析验证。在多混合单元的设计方案下，如图2所示，两种不同浓度溶液的混合效果随混合驱动路径增加逐渐叠加，在出口处浓度分布呈现有效混合。数值实验结果表明，所设计的电渗流微混合器的混合评价指数在0.05以下，满足不同浓度溶液完全混合的设计需求。

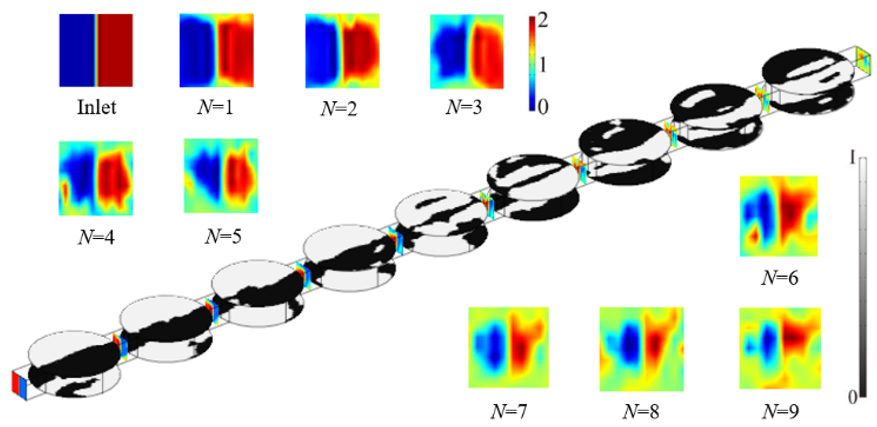
图2：多混合单元（ N=9）电极版图和不同混合单元模型方案出口浓度分布

▍研究前景

本文研究基于拓扑优化方法，建立电渗流微混合器模型，设计优化电极版图。该种电渗流电极设计方法减少优化设计过程中对设计者经验的依赖，满足不同浓度微流体完全混合的设计需求，在陆空技术方面有着重要应用价值。

▍研究团队介绍

团队基于改进的拓扑优化设计方法设计微纳功能器件，这些器件的研究涵盖众多学科，如光学、流体力学等。

在光学方面，团队利用拓扑优化研制超构透镜，试图解决目前超构透镜存在版图数据量大、难以加工、效率低、色差等问题。针对以上问题，团队利用拓扑优化寻找平衡色散、转换效率的微纳单元结构，基于几何相位设计了531~ 780 nm的消色差超构透镜，该透镜在目标波段内的平均效率达到53%[3]，显著优于目前同类别的超构透镜。团队利用拓扑优化设计的同心纳米环超构透镜，具有低的占宽比，版图数据量小等优点。相比已有的设计方法，同等占宽比的情况下该设计方法获得透镜性能更优。基于该方法团队已经研制出口径为1 mm，数值孔径0.8，分辨优于600 nm的可见光宽谱超构透镜[4]。针对超构透镜实用化面临的口径难以做大的技术瓶颈问题，团队基于单元拼接的方法[5]研制了口径1 cm和2 cm的可见光与红外超构透镜。口径1 cm的红外超构透镜工作波段为8~12 μm，F#为1，分辨率优于0.12 lp/mrad，口径1 cm的可见光超构透镜成像清晰。截至目前，团队已经具备厘米、分米口径超构透镜的研制能力。

图3：团队研制的超构透镜相机样机与成像结果

团队也通过内部开发的拓扑优化算法设计金属、介质等微纳结构用于电磁场增强、光学异常透射、光学波导、电磁隐身等相关应用[6-9]。这些研究工作对于在集成光子学领域中构建光学传感器件以及利用微纳结构操纵和引导光具有指导意义。

在流体力学方面，团队提出了基于连续伴随分析的流体力学拓扑优化方法，解决了固液界面纹理的设计难题，并原创的提出了流形上的拓扑优化方法，将拓扑优化的结构设计空间扩展到了二维流形上[10-12]。利用以上方法团队进一步提出了获取周期性固液界面纹理微结构的严格数学模型，通过极小化液汽界面所支撑液体凸起的体积，增强了纹理化固体表面的储气能力，这些工作对疏水表面研制和流体力学减阻具有重要意义[13]。

图4：表面微纳结构及固体表面液体黏附力的对比实验

团队已经将多年在拓扑优化领域的研究成果整理出版了两本学术专著[14,15]（Adjoint Topology Optimization Theory for Nano-Optics ；Topology Optimization Theory for Laminar Flow），感兴趣的读者可以阅读。

图5：团队出版的两本拓扑优化领域的学术专著

▍论文信息

孙建文, 张健宇, 李博文, 等. 基于拓扑优化的电渗流微混合器电极[J]. 光学精密工程, 2023,31(17):2515-2524. DOI：10.37188/OPE.20233117.2515.

https://ope.lightpublishing.cn/thesisDetails#10.37188/OPE.20233117.2515

▍作者简介

邓永波，中国科学院长春光机所研究员、博士生导师，入选2018年德国洪堡资深学者；以第一作者出版Springer英文专著2部；在 CMAME、JCP等权威期刊和IEEE MEMS、Transducers等领域顶级国际会议上累计发表论文60篇，获得授权中国发明专利14项；入选2022年中国科学院稳定支持基础研究领域青年团队；获得2016和2017年卡尔斯鲁厄理工大学客座教授奖；入选中国科学院青年创新促进会会员和IEEE学会、中国微纳技术学会等高级会员。

▎参考资料

[1] Deng, Y., et al., Topology optimization of electrode patterns for electroosmotic micromixer. International Journal of Heat and Mass Transfer, 2018. 126: p. 1299-1315.

[2] Sun, J., et al., Topologically optimized electrodes for electroosmotic actuation. Journal of Advanced Manufacturing Science and Technology, 2023. 3(1): p. 2022022-2022022.

[3] Zhang, L., et al., High-Efficiency Achromatic Metalens Topologically Optimized in the Visible. Nanomaterials (Basel), 2023. 13(5).

[4] Jin, Z., et al., Topologically optimized concentric-nanoring metalens with 1 mm diameter, 0.8 NA and 600 nm imaging resolution in the visible. Opt Express, 2023. 31(6): p. 10489-10499.

[5] Wang, C., et al., Fabricable concentric-ring metalens with high focusing efficiency based on two-dimensional subwavelength unit splicing.Opt Express, accepted.

[6] Deng, Y. and J.G. Korvink,Topology optimization for three-dimensional electromagnetic waves using an edge element-based finite-element method. Proc Math Phys Eng Sci, 2016. 472(2189): p. 20150835.

[7] Lin, Y., et al., Topologically optimized periodic resonant nanostructures for extraordinary optical transmission [Invited]. Optical Materials Express, 2021. 11(7): p. 2153-2164.

[8] Han, Y., et al., Nanoantennas Inversely Designed to Couple Free Space and a Metal-Insulator-Metal Waveguide. Nanomaterials (Basel), 2021. 11(12): p. 3219.

[9] Chen, Y., et al., Topology Optimization‐Based Inverse Design of Plasmonic Nanodimer with Maximum Near‐Field Enhancement. Advanced Functional Materials, 2020. 30(23).

[10] Deng, Y., Z. Liu, and Y. Wu, Topology optimization of steady and unsteady incompressible Navier–Stokes flows driven by body forces.Structural and Multidisciplinary Optimization, 2012. 47(4): p. 555-570.

[11] Deng, Y., et al., Topology optimization of steady Navier–Stokes flow with body force. Computer Methods in Applied Mechanics and Engineering, 2013. 255: p. 306-321.

[12] Deng, Y., Z. Liu, and J.G. Korvink, Topology optimization on two-dimensional manifolds. Computer Methods in Applied Mechanics and Engineering, 2020. 364: p. 112937.

[13] Deng, Y., et al., Inversely designed micro-textures for robust Cassie–Baxter mode of super-hydrophobicity. Computer Methods in Applied Mechanics and Engineering, 2018. 341: p. 113-132.

[14] Deng, Y., Adjoint Topology Optimization Theory for Nano-Optics. 2022, Singapore: Springer, Singapore.

[15] Deng, Y., Y. Wu, and Z. Liu, Topology optimization theory for laminar flow. Springer Singapore, Singapore, 2018. 10: p. 978-981.

阅读原文