几何在物理学中的妙用

原创 董唯元 返朴

物理学发展到20世纪，数学中的几何被引入到物理理论中。爱因斯坦借助黎曼几何构建了广义相对论，杨振宁发现规范场与纤维丛的对应关系，而到1980年代后拓扑量子场论的诞生，又将物理学推向了新的高峰。几何理论和相关概念在物理理论中大显身手，以至于有很多人说“物理就是几何”。如今这些由几何诞生的物理概念，已经深入到大气科学、信息科学等许多领域，也为几何学带来新的生命力。

撰文 | 董唯元

物理理论经常会被跨领域借鉴使用。近几年气象学家在研究海洋和大气波动规律时，将地球类比为拓扑绝缘体[1-3]，从而借助物理学家研究拓扑相变的方法和结论，深刻理解了赤道开尔文波的形成机制。

开尔文波是一种因地球自转偏向力（即科里奥利力）而形成的海洋和大气波动。其最大的特点就是群速度与相速度相同，所以这种波不会在行走的过程中耗散，能够跨越数千公里持续搬运能量，是形成厄尔尼诺等气候现象的重要因素之一。

其实这种波早在1879年就已被发现，并以发现者命名。没错，发现者正是那位科学全才——开尔文勋爵，绝对温标也是以他名字命名的。相信老勋爵一定不会想到，100多年后他所发现的海洋和大气波动，竟然以如此奇特的方式与现代物理学产生联系。即使老勋爵乘坐时光机来到当下，估计也不能快速理解为什么开尔文波竟然是一种“拓扑保护下的激发”。

现代物理学中几乎无处不浸染着几何概念和几何语言，其深度和广度是十九世纪的物理学家根本无法想象的。

微分几何进入物理学

1915年横空降世的广义相对论，是物理学几何化的第一个里程碑，微分几何从此成为物理学家必须掌握的一门数学语言。

既然引力的本质是时空弯曲，引力场强是时空曲率，那么摆弄弯曲流形的学问，自然成了学习广义相对论的首要预备知识。所谓流形（manifold），可以认为就是各种各样的图形。比如土豆的表面是2维流形，而广义相对论所研究的时空则是4维流形。

为了能够计算，必须得在流形上建立坐标系。如果流形本身形状比较奇怪，或者坐标系覆盖能力有限，仅用一个坐标系无法覆盖流形上所有的点，那么就需要在流形上选取多个点，每个点都可以建立局部坐标系覆盖周边邻居，再把所有局部坐标系拼贴起来以覆盖整个流形。

比如，以地球某时刻为原点的4维笛卡尔坐标系，就无法覆盖到远处黑洞的内部，即使经历无穷长时间也只能到达很靠近黑洞视界的地方。然而这并不意味着时空本身在视界处被撕裂。靠近黑洞视界的宇航员可以以他自己的位置和某时刻为原点建立新的坐标系，这个坐标系既与我们的坐标系有交叠，又同时与黑洞内的其他坐标系有重合。借助多个坐标系共同承托，就可以画出一条光滑的世界线，连接地球和黑洞内部，从而看出视界处时空本身仍然完好无损。

另外，要想讨论曲率，得先让流形固定不动，蠕动着的水母表面显然不会有确定的曲率。而定型的含义等价于“流形上任意两点之间存在确定的距离”，于是流形上关于距离的定义必然要先于曲率的定义。

我们知道在最简单的x-y平面上，距离的定义是

。类似的，可以猜测弯曲平面上的局部坐标系里，哪怕坐标轴不正交，反正总可以把距离写成状如

的样子，这个α、β、γ组合，就叫作“度规”（metric），它回答了流形上每点与临近的点之间该如何计算距离的问题。如果流形上每一点都有了自己的度规，那么整个流形也就被“石化”了，此时才可以计算曲率。

数学上对曲率的定义有若干种，物理学家最喜欢使用黎曼的定义方式。黎曼曲率可以用向量在移动过程中的变化来体会，所以在了解它之前，我们还需要先了解流形的弯曲会对向量的移动造成什么影响。

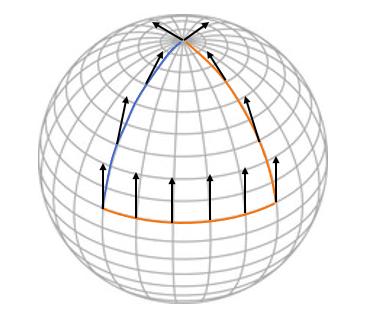
平直空间中向量可以随便平移都不会发生改变，可是在弯曲空间中这种自由就不存在了。例如在上图所示的球面上移动向量，同样从赤道上出发开始“平动”（注意2维球面内的向量方向只能切于球面），经过橙色路径后到达北极的指向与经过蓝色路径到达北极的指向并不相同，这就是由球面的弯曲造成的效果。

黎曼曲率就是利用这种效果来定义流形上每点的曲率。具体做法是让初始向量ν0从自家位置P点出发，沿着闭合环路在家附近溜达一圈再回家，旅行之后的向量就会与出发前的向量有所差别。我们用向量Δν=ν'0-ν0代表这个变化量。

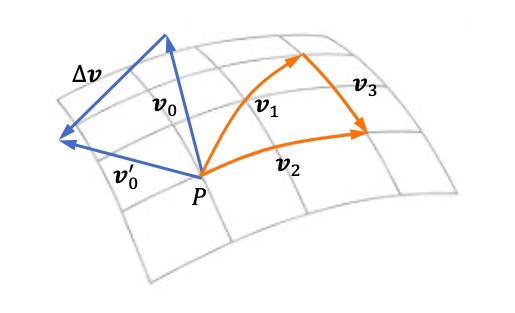
构成闭合旅行线路最少还需要两个独立向量ν1和ν2，只要这个闭合路线足够小，我们可以马马虎虎地把ν3也看作P点处的向量ν3=ν2-ν1。这样ν1、-ν2和ν2-ν1就构成一个闭合的旅行路线。

总之，在P点处只要给出三个向量ν0、ν1和ν2就对应一个确定的Δν。这显然是一个映射，从三个向量到一个向量的映射。提供这种映射功能的“机器”叫作张量（tensor），黎曼曲率就是张量，所以也被称为黎曼张量。顺便提一下，前面说到的度规也是张量。其实整个广义相对论方程就是张量方程。

纤维丛与规范场

1954年闪亮登场的杨-米尔斯理论，为后续物理学几何化的第二次浪潮埋下了伏笔。十几年之后，物理学家突然发现纤维丛正是描述这一理论最恰当的语言。

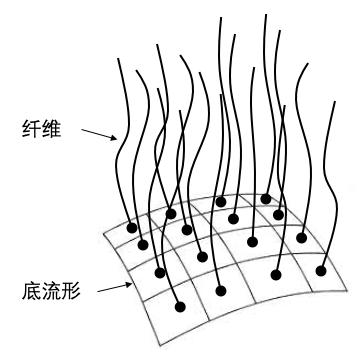
所谓纤维丛（Fiber bundle），可以简单粗暴地理解为浑身长毛的流形，每根毛对应底流形上一点。这里的毛，也就是纤维，具有颇为抽象的内涵，在不同的纤维丛理论中代表流形身上不同的附加物。这些附加物既可以是天生的，也可以是后天装饰上去的。

最直观的一种纤维，就是流形上每一点的切空间（tangent space），顾名思义是此点处所有向量生活的空间。下图左侧画出的是个具体例子，其中底流形M是2维球面，蓝色平面是M上P点的切空间，记做TP(M)；橙色平面是Q点的切空间，记做TQ(M)。右侧是对这种关系的抽象画法。

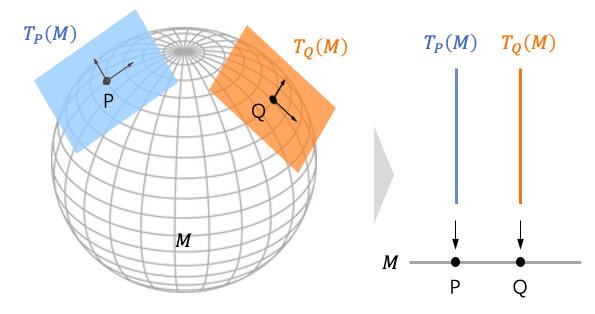
前面在介绍曲率的时候曾经含混地提到向量在流形上的“平动”，其实那种说法非常不严谨。P点的向量无论怎么变，都始终是TP(M)的元素，没办法跑到TQ(M)里，所以讨论向量在流形上的移动之前，要先规定TP(M)与TQ(M)之间的关系。这种纤维与纤维之间的关系叫作联络（connection），切空间之间的联络就约定了流形上怎样的向量移动算是平动，在约定之后才能计算曲率。

切丛的概念直观易懂，但还不是物理学家的强大武器，真正使物理学家爱不释手的，是一种能够包含对称性的纤维丛。因为它过于核心重要，所以干脆被命名为主丛（principle bundle）。

谈论对称性时，我们需要注意区分全局对称性（global symmetry）和局域对称性（local symmetry）这两个完全不同的概念。前者是整个流形总体所拥有的对称性，而后者则是每个点各自具备的属性。后面的内容会展示出，局域对称性在物理中的重要地位要远大于全局对称性。

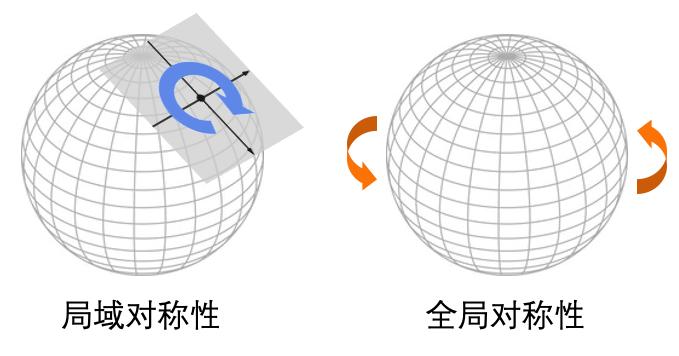
描述对称性的数学语言是群，每一种对称性都对应特定的群。例如O(n)群和SO(n)群对应着n维实数空间中的旋转对称，而U(n)群和SU(n)群则代表n维复数空间中的旋转对称。

我们所身处的3维空间中，任何转动操作都可以拆解为绕x、y、z轴转动这三种基本操作的某种组合。也就是说，如果把SO(3)群自己也看作一个空间的话，维数恰好也是3维。可是SO(4)群却不同，4维空间中的转动由6种基本操作组合而成[4]，所以SO(4)群本身的维数是6不是4。

群本身也可以被看作一个空间，就像那个直观的切空间一样，所以也就能当作纤维插在底流形上，只不过每根纤维所代表的空间与底流形可能具有不同的维度数量。

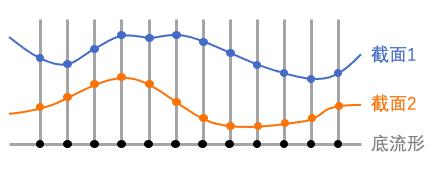
这种插着群结构的纤维丛就是主丛。纤维所代表的局域对称性意味着，底流形上的函数Φ(x)，沿着纤维变动时，每个点上Φ(x)的值保持不变，所以主丛上的不同截面对Φ(x)来说是等价的。在物理上，像Φ(x)这样具有局域对称性的场统称为规范场（gauge field）。

在物理学家眼中，时空本身就是一个纤维丛，各种基本相互作用就源自各种规范场，也就是携带不同对称群的主丛的联络。引力场对应SO(3, 1)，电磁场和弱力对应U(1)×SU(2)，强力对应SU(3)。

后面两者合并起来，携带U(1)×SU(2)×SU(3)结构的主丛整体是一个大空间，在这个空间里，宇宙中除引力之外的其他相互作用都漂亮地合并为一个对象。这就是堪与广义相对论比肩的杨-米尔斯理论，是基本粒子标准模型最重要的理论基石。

来自拓扑理论的加持

拓扑学常被戏称为玩弄橡皮泥的科学，它并不关心几何图形具体的形状或大小，而只关注图形在连续变化过程中那些不变的成分。咖啡杯可以连续地变成甜甜圈，所以在拓扑视角看来，咖啡杯与甜甜圈就是同一种对象，因为二者身上孔洞的数量相同。显然，孔洞的数量就是一种拓扑不变量。

不过数学家在说某甲和某乙在拓扑意义上相同时，会使用不同的术语来表达“相同”这个含义，常见的有同构、同胚、同态、同伦、同调等等。由此可以窥见，拓扑理论并不像捏橡皮泥那么简单。

另外，在数学这棵大树上，拓扑理论的位置并不是边界清晰的某一分支，甚至不仅限于几何学领域之内，而更像是四处缠绕的藤蔓。也正因如此，它往往能在许多问题上发挥出避繁就简的奇特威力。

有个名为“毛球定理”的有趣定理，内容是说，偶数维球面上的光滑切向量场必有零点。这个定理的2维情形非常直观，其实就是说永远无法完全抚平一个毛球，定理的名字正是因此而得。

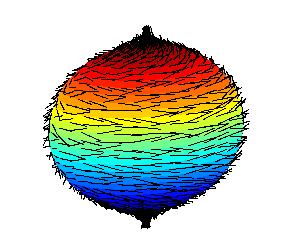
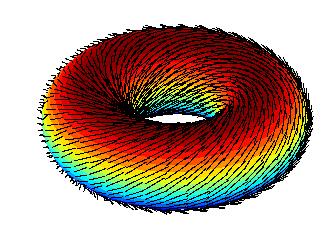
作为对比，我们可以同样直观地看到，圆环面上的切向量场就可以处处非零，这说明流形的整体拓扑性质与其上向量场的特性有密切联系。

如果读者感觉这个定理不过如此的话，不妨考虑由点源发出的电磁波，其波阵面就是一个2维球面，而且电磁波是横波，场强方向总是切于波阵面。根据毛球定理，在波阵面上必有场强零点[5]。可是，波阵面上的每一点都有相同的振动相位，而且对点源来说，都是完全对称的。是不是嗅到了魔术的味道呢？

当电磁波在某些特殊介质中传播的时候，其参数空间中也会出现这种适用毛球定理的情形。尽管描述动力学过程的一堆偏微分方程难以求解，但是仅凭拓扑性质就可以判断零点一定会出现。这种纯粹由拓扑性质所催生的特殊点往往对应着某种“拓扑激发”。

拓扑理论之所以能够发挥出巨大威力，凭借的是将各种拓扑不变量与物理场中的各种积分结果建立起联系。从文章前面的部分已经提过，物理场中的场强对应几何意义上的曲率，距离关系对应着度规。如果物理场中的某种积分结果与场强和积分路径长度都无关，那么翻译成几何语言就是，结果无关流形的曲率和度规，所以即使这个流形像水母一样蠕动起来，积分结果也不会变化，那么这个结果应该就只由流形的某种拓扑不变量决定。

基于这样的思想，物理学家非常热衷于研究各种各样的积分结果，尤其是闭合环路或者闭合曲面上的积分结果。如果确实发现了某个与场强和路径长度都无关的物理量，人们就会兴冲冲地跑去拓扑学的仓库中寻找与之相关的拓扑不变量。

关于积分路径，聪明的物理学家们肯定不甘心手工逐个慢慢尝试，而是喜欢运用能够“批发”的研究策略。

我们先从一个傻问题开始。在一个平面上，从一个定点出发，画一个闭合的曲线并最终回到定点，能有多少种画法呢？答案很明显，任意两种画法之间都是拓扑意义上相同的，用术语来说，所有路径都是同伦的。

如果在平面上挖去一个洞，所有的路径显然就不再同伦，因为有些路径可以收缩成一点，而有些路径在收缩时会被洞挡住，无法收缩成一点。我们发现所有的路径可以按照绕洞圈数分成若干类，绕洞圈数相同的路径之间都同伦。

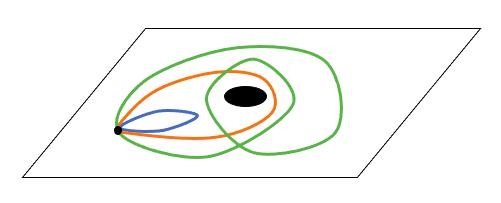
这个幼儿园级别的一笔画游戏其实有个很拽的专业术语，同伦群（homotopy groups），记做πn(X)，意在表示流形X上，过定点的n维闭合面（1维时就是闭合线）的同伦情况。

通过刚才的例子已经知道，π1(简单平面)=0，意思是说所有闭合路径都只同伦一种情况，而

，意思是说这个同伦群可以用所有整数来表示，每个整数代表绕数为该整数的同伦路径，因为绕行有分顺时针和逆时针，可以两相抵消，所以天然存在负整数的绕数。

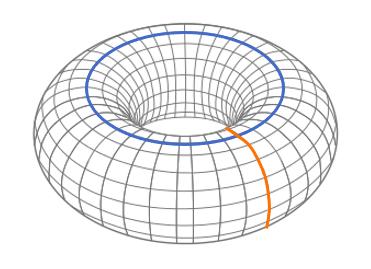
另外读者还可以验证一下

，原因是圆环面在橙色方向和蓝色方向各有独立的绕数。

这里只是列举了同伦群中情况最为简单的几种，当X的维数和n变大时，πn(X)的复杂性会爆炸式增加，即使只增加X的拓扑复杂性，也会让πn(X)变得难以计算。有兴趣的读者可以自行琢磨一下π1(简单平面扣掉2个点)，看看会遭遇到什么困难。

与同伦群味道类似的概念还有一个同调群（homology groups），记做Hn(X)，大致与连通性和孔洞的数量相关。限于篇幅，对这个概念就不做介绍了，只稍微提一下流形上的孔洞数量，以及刚才那个一笔画游戏中的缠绕数，这些都是典型的拓扑不变量。此外绳结理论中对绳结的分类等，也属于拓扑不变量。

最直观的一个拓扑不变量是小学奥数中就已经出现过的“欧拉示性数”，3维凸多面体总满足V-E+F=2，其中V是顶点数，E是棱边数，F是面数。因为3维凸多面体的表面都同态于2维球面，所以它们都拥有相同的欧拉示性数

。欧拉示性数与流形身上孔洞的数量有个简单的换算关系，

，这个g就是孔洞数。

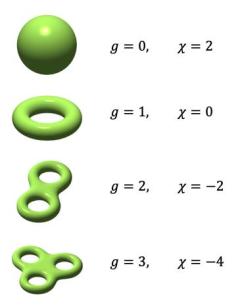
不过欧拉示性数相同的流形未必全都同态，比如1维环、2维环面、莫比乌斯带和克莱因瓶，这些流形的欧拉示性数都是0，但它们显然不同态，甚至一些基本属性都大相径庭。

除了欧拉示性数之外，还有许许多多的拓扑不变量，受篇幅和本人学识所限，就不再列举了。但有一个对现代物理学非常重要的拓扑不变量必须得提，那就是陈-西蒙斯作用量（Chern-Simons action）。

从这个名字就能看出，这个拓扑不变量天然就对应一个物理上的积分，n维场的作用量

，其中

是拉氏量密度。而且这不是普通的积分，而是生成整个物理场一切动力学属性的核心，从最小作用量原理出发推导出运动方程的套路相信许多读者都已经烂熟于胸了。

至于这个拓扑不变量为什么天然对物理学如此友好，那是因为它出自物理学家之手——由目前唯一获得过菲尔兹奖的物理学家威滕所发展而来。当然，他的工作基础大量来自于陈省身等人前期成果，尤其是一个名为“陈-西蒙斯3-形式”的数学对象，所以这套由威滕等人引入物理学的理论，仍被称为“陈-西蒙斯理论”。

正是以此为核心，威滕和施瓦茨等人为量子场论开辟出了一个全新的分支——拓扑量子场论（TQFT）。从某种意义上说，拓扑量子场论的出现，也进一步加重了整个现代物理学的几何色彩。

小结

在近几十年的发展过程中，现代物理学与现代几何理论不仅相辅相成共同成长，而且还一同发展出许多通用性更强大的理论工具，广泛服务于信息科学、经济学、社会科学等领域。文章开头提到的气象学研究成果，正是拓扑量子场论为这一领域做出的贡献。

杨振宁曾经对陈省身说：“非交换的规范场与纤维丛这个美妙的理论在概念上的一致，对我来说是一大奇迹。特别是数学家在发现它时没有参考物理世界。你们数学家是凭空想象出来的。”陈省身却立刻加以否认：“不，不，这些概念不是凭空想象出来的，它们是自然的，也是真实的！”

参考文献及注释

[1] Delplace, P., Marston, J. B., & Venaille, A. (2017). Topological origin of equatorial waves. Science, 358(6366), 1075–1077. https://doi.org/10.1126/science.aan8819

[2] Tong, D. (2022). "A Gauge Theory for Shallow Water". arXiv:2209.10574.

[3] McCormick, Katie (July 18, 2023). "How Quantum Physicists Explained Earth's Oscillating Weather Patterns". Quanta Magazine.

[4] 4维空间中的转动轴是一个面而不是一条线，4条坐标轴两两组合，共有6个基本轴面。

[5] Bormashenko, Edward (2016-05-23). "Obstructions imposed by the Poincaré–Brouwer ("hairy ball") theorem on the propagation of electromagnetic waves". Journal of Electromagnetic Waves and Applications. 30 (8): 1049–1053. Bibcode:2016JEWA...30.1049B. doi:10.1080/09205071.2016.1169226. ISSN 0920-5071. S2CID 124221302

本文受科普中国·星空计划项目扶持

出品：中国科协科普部

监制：中国科学技术出版社有限公司、北京中科星河文化传媒有限公司

版权说明：欢迎个人转发，任何形式的媒体或机构未经授权，不得转载和摘编。转载授权请在「返朴」微信公众号内联系后台。

原标题：《几何在物理学中的妙用》

阅读原文