解释城市｜从齐普夫法则看大城与小城

纽约街头。视觉中国 资料图

在城市和区域科学中，齐普夫法则（Zipf law）是一个简单而又复杂的存在。说它简单，是因为它的表现形式简单、直观、普适；说它复杂，是因为有关齐普夫法则的机理性解释一直争论不休，甚至到目前为止也没有十分完美的解释。各国的现实情况与齐普夫法则的对应性和适应性也被广泛讨论。 

一、什么是齐普夫法则?

通俗来说，一个国家人口最多的城市人口数量通常是第二多城市人口数的2倍，是第三多城市人口数的3倍，是第四多城市人口数的4倍……以此类推。简言之，人口规模位次排名首位城市人口数量是位次排名第n位城市的人口规模的n倍，这里面涉及到两个量，排名的位次和人口的规模，所以也称为位次-规模法则。齐普夫法则得名于美国的语言学家G. K. Zipf，在他的1949年的一本书《人类行为与最小努力原则》中，提出了一个观点，人们总是很懒，做一件事总是希望付出最小努力，比如想表达一个观点，总是希望用最少的语言和词汇，这样的一种后果就是少数几个单词大量重复，而不得已才会用一些复杂的词汇，所以一些词汇出现的次数就相当少。他统计了书中单词，发现了上述与城市人口位次-规模差不多的结论，一本书中出现次数最多的单词的次数是出现第二多单词的次数的2倍，是第三多单词的3倍……后人为了纪念他提出的“最小努力”原则就把该现象称为“齐普夫法则”（Zipf’s law）。其实，城市领域这种现象发现要比齐普夫单词现象要早，城市的人口位次与规模之间的关系第一次被明确记录是1913年在德国物理学家奥尔巴赫（Felix Auerbach)的文章《人口集中定律》（德文名称 Das Gesetz der Bevölkerungskonzentration）中，他第一次系统分析了1910年德国94个城市规模和位序之间的关系，发现这些城市的规模和位次的乘积是一个常数。

如果用数学符合和图形来表达齐普夫法则就更有意思了。数学上假设排名为n的城市人口为y，那么数学表达成 n=A*y^(B)（A和B都是参数），如果是完美符合齐普夫法则，那么B=-1，这时候n*y=A，就是上面奥尔巴赫发现的规模和位次的乘积是一个常数。在图形上，如果把位次n作为纵坐标，人口规模y作为横坐标，放在双对数坐标系中，会得到一条完美的斜率为-1的直线（如下图那样），之所以要放在双对数坐标系中，是因为n=A*y^(B)经过双对数坐标系变换就是一个我们很熟悉的线性方程。其实，双对数坐标系起到一种“降维”的作用，现实世界的很多复杂关系通常不是线性的，而是高维非线性的，人们为了处理方便，通常采用对数坐标使得高维的非线性回归到低维的线性过程。

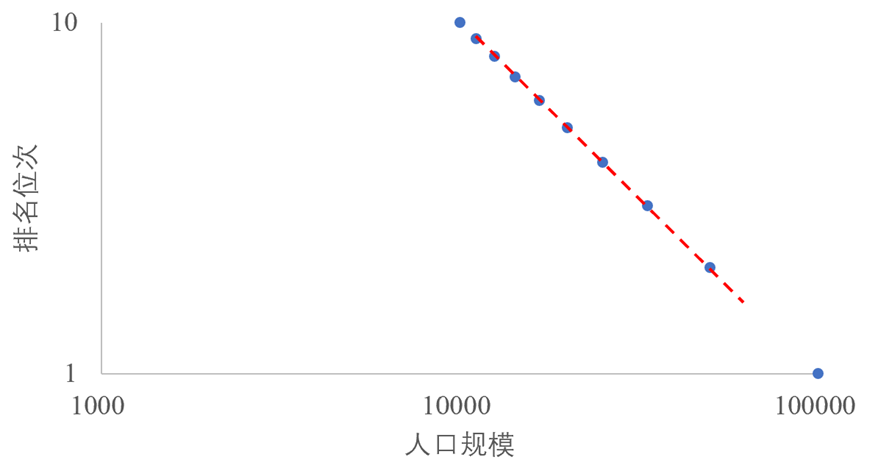
图1  一个完美的齐普夫法则线    资料来源：笔者绘制

二、是什么造就了齐普夫法则？

对齐普夫法则的机理性解释或者动力学原因阐述一直饱受关注和争论。一方面，它背后的机理也许直接关系到“财富为什么总是不均衡分布”“为什么上市公司少数头部企业集中了大部分利润”等一系列有关“不平衡”和马太效应的现象。另一方面，不同阶段对于齐普夫法则的认识通常会不一样。比如，早期齐普夫本人在那本书中提出的人类“最小努力”原则算是一个解释。这里笔者介绍几个城市科学领域比较知名的解释。第一种解释是由卡耐基梅隆大学的经济学家，同时也是1978年诺贝尔经济学奖获得者的哈伯特·西蒙（Herbert. A. Simon）在1955年提出的随机增长（Random growth）理论，1999年哈佛大学教授Xavier Gabaix在此基础上进一步证明和完善。他们认为不管这些城市一开始的规模如何，只要他们的发展按照同一种模式进行随机增长，最终必然会导致这些城市之间人口规模符合齐普夫法则，换言之，大城市的增长速度未必比小城市慢。当然，大城市的增长速度也未必比小城市快，他们的快慢完全是一种随机性的，经过长时间随机增长之后，随机效应逐步累积，城市之间的分化就产生了，便出现了超大型城市，大型城市等完整的等级体系。他们还解释了为什么有的国家内城市实证结果完美符合齐普夫法则，而有的却不是，主要差别在于有没有新的城市产生，如果没有新城市产生，就比较符合齐普夫法则。如果人口增长过程中增量人口产生了新的城市就会偏离齐普夫法则。

当然，该理论也并非无懈可击，首先他没有考虑到人口流动问题，城市人口的增量除了来自自然增长部分还有人口的净流入部分，如果说大城市和小城市的人口自然增长率满足同一种分布特征尚且可以理解，但是人口的净流入该如何影响城市人口分布呢？2020年两位法国学者Verbavatz和Barthelemy在《自然》（Nature）杂志上发文称，齐普夫法则主要是由大规模的人口流动主导的，他们就按照上述的人口增长动力学考虑了净流入的人口，发现人口流动对城市人口增长的影响更大。其实，早在1998年，瑞士弗里堡大学的Matteo Marsili和张翼成教授就发现人口个体之间的社会交互是产生城市齐普夫法则的重要原因。

2021年德国、意大利和巴西的几位学者提出了一个非常有意思的最大多样性理论（Maximal diversity），他们认为，城市人口之所以这么分布是取得系统多样性最佳的一种选择。举个例子，假设现在有10个人，分布在3个城市，会有几种分配方法？比如3+3+4、4+4+2、1+2+7、2+3+5……哪一种分配方法更好呢？他们认为3+3+4和4+4+2的分配方案里面只出现了2个不同的数字，多样性为2，而1+2+7和2+3+5有3个不同的数字，多样性为3。因此，后两者的分配多样性要优于前两者的分配方案。因此，他们通过模仿物理学中粒子配分方法，采用数学模拟发现国家总人口按照齐普夫法则的分配方法分配到各城市能够让系统多样性取得最大。

这些理论从不同的角度分析了齐普夫法则产生的机制，丰富和发展了相关的理论，但每种理论也有各自的局限性和不足，这也从侧面印证了齐普夫法则看似简单实则暗藏玄机。 

三、中国城市的规模和位序符合齐普夫法则吗？

自从奥尔巴赫1913年发现德国城市的齐普夫法则以来，有关各国的城市位序和规模之间关系的实证研究就汗牛充栋。笔者在Web of Science （一个英文学术文章检索工具）中输入Zipf’s law 发现从1991年到2021年研究热度一路走高，2021年达到高峰。

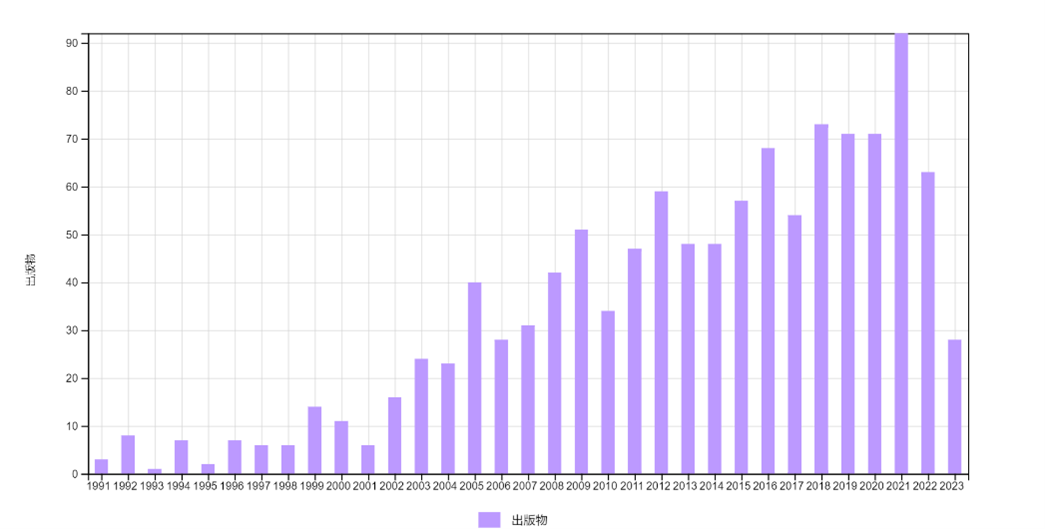
图2  在Web of Science 中检索“Zipf’s law”历年发表的文章数量。资料来源：Web of Science

较早之前，有学者指出行政体系主导的城市如苏联和中国的城市规模不太服从齐普夫法则，但从1995年以来中国地级市及以上的城市人口规模和位序关系看，中国城市还是基本符合齐普夫法则的，比如有学者分析了1995-2015年每隔2-3年中国城市人口规模分布，发现基本吻合齐普夫法则，但是相比较美国、印度等城市吻合程度略低一点。为此，笔者用2020年第7次人口普查的数据做了验证。很明显，中国的城市分布“部分”吻合齐普夫法则，吻合的部分主要是人口规模大于500万以上的城市，或者排名在210名之前的，但是即使这部分吻合，其斜率参数（即B）与完美的齐普夫法则预计的-1也有明显偏颇。头部城市如人口最多的重庆3205万人，是第二位上海2487万和北京2189万的1倍多一点，与齐普夫法则预测的并不十分相符。反观同时期美国的城市则非常符合齐普夫法则，连斜率参数也与齐普夫法则预计的-1相差无几，尤其是头部城市，比如美国人口最多的纽约人口823万，正好是第二位洛杉矶人口398万的2倍左右，是第3位芝加哥267万的3倍左右。

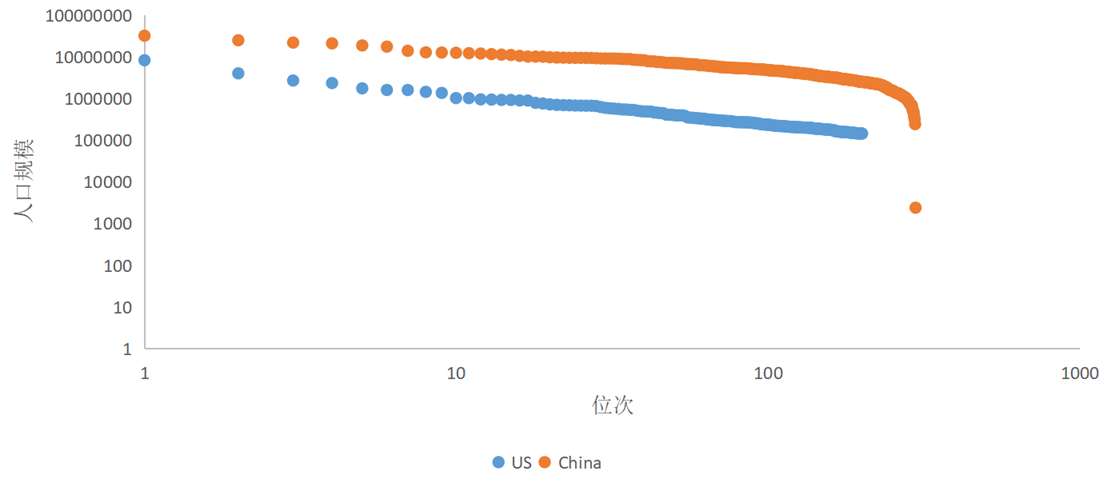
图3  中国第七次人口普查的地级市以上城市和美国2020年城市的人口位序-规模关系
资料来源： 笔者根据第七次人口普查数据整理，美国数据来自美国统计局。

最后，笔者认为齐普夫法则在一定程度上能够解释城市之间规模的特征，但不同的国家情况也会对该法则的普适性形成一定的挑战。除了城市人口数量的齐普夫法则被发现，城市领域的很多变量都是按照齐普夫法则进行分布，这又将涉及到城市科学中的标度律问题。

（作者戴跃华系上海发展战略研究所博士。感谢上海财经大学张洁同学对本文部分数据的整理。）

-----

“解释城市”专栏由上海发展战略研究所戴跃华博士主持，关注城市科学发展的前沿趋势，解释城市科学以及城市中人类行为动力学的一般特征和规律，探究利用前沿城市科学理论优化城市治理的路径和方法。