- +1
大模型也有好玩的数学,从麦克斯韦的最低势能问题到人机对齐
机器之心专栏
机器之心编辑部
在本篇文章中,来自斯坦福大学、普林斯顿大学和宾夕法尼亚大学的研究者们联合发表了一篇论文,分析了大型语言模型对齐中的“奖励坍缩”现象。
将 ChatGPT 与人类价值观对齐 (RLHF) 的过程中,很重要的一步是人工生成对答案偏好的排序,并且训练一个奖励模型 (reward model) 学习人类的偏好。近期的一个研究表明,基于排序偏好的人机对齐,其优化问题几乎等价于电磁学之父麦克斯韦在一百多年前考虑过的问题:将若干个带同号电荷的粒子限制在 0 到 1 的区间内,这些电荷将如何分布以达到最低势能?这个问题也跟菲尔兹奖得主 Stephen Smale 的第七问题密切相关。
一种被称为 “奖励坍缩” 的现象理论上会在训练大型语言模型的 RLHF 过程中发生,这一现象的背后和优化理论以及物理中的麦克斯韦问题 (又称为汤姆孙问题) 息息相关。这可能会妨碍模型对人类反馈的准确解析。为了解决这个问题,作者提出了一种新的、根据输入的提示调整奖励分布的优化方法。

论文地址:https://arxiv.org/pdf/2305.17608.pdf
奖励坍缩现象
我们已经进入了大型语言模型 (Large Language Models) 的时代,ChatGPT 和 GPT-4 等模型的出色能力已经改变了我们许多人的工作生活方式。这些模型能够比较好地理解和反馈人类指令的背后,离不开 RLHF (Reinforcement Learning with Human Feedbacks)。RLHF 先通过人类的反馈训练一个奖励模型,再通过强化学习的方法训练出更好的大型语言模型。这其中的奖励模型基于人类偏好进行训练,描绘出人类的价值观、道德考量,然后引导语言模型进行微调和学习。
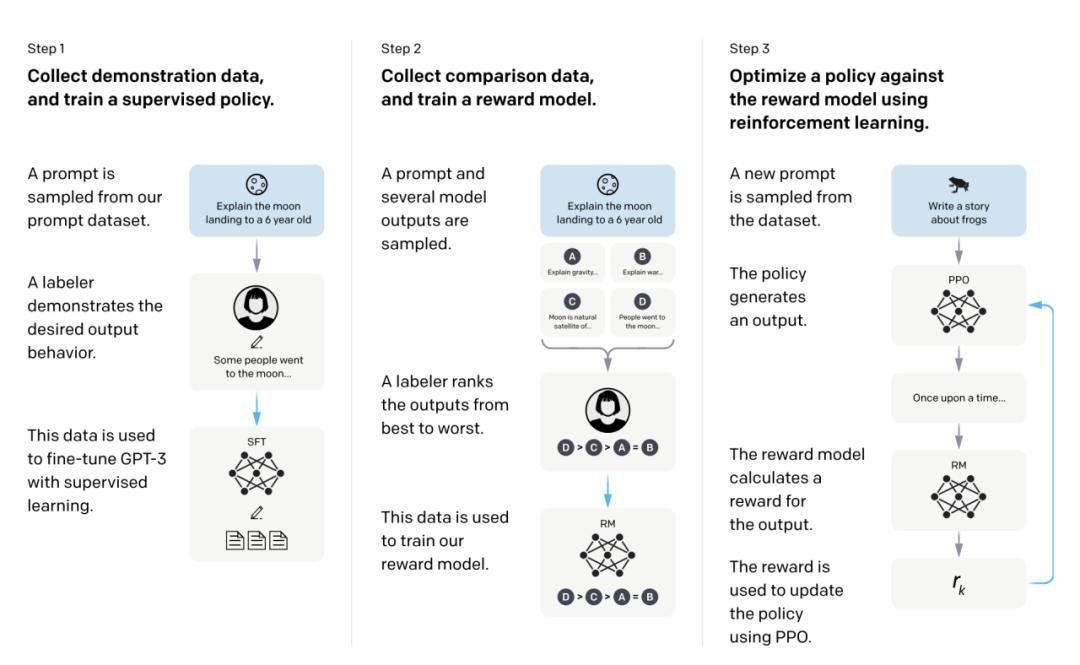
Figure 1 InstructGPT 中的 RLHF
然而,基于人类偏好构建有效的奖励模型并非易事。尤其是当人工标签者需要对某个特定提示 (Prompt) 的回应进行定量评分时,他们往往难以做出决策。相反,人们更容易做出针对两个回应的比较,例如在 InstructGPT 的开发过程中,人工标签者会对同一提示下模型产生的多个回应进行排名,从最好到最差,并训练出一个奖励模型来尽可能准确地反映这种排名。
训练奖励模型的方式是最大化如下的函数:其中效用函数 U 通常被取成 Sigmoid 函数的对数
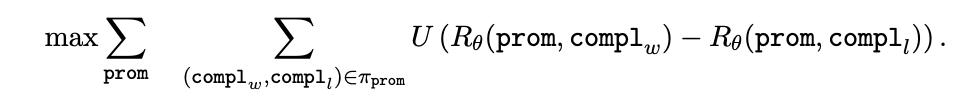
Figure 2 训练奖励模型的优化问题
例如当效用函数是 - 1/x (x>0) 的时候,对固定的 n, 奖励的分布如下图所示:
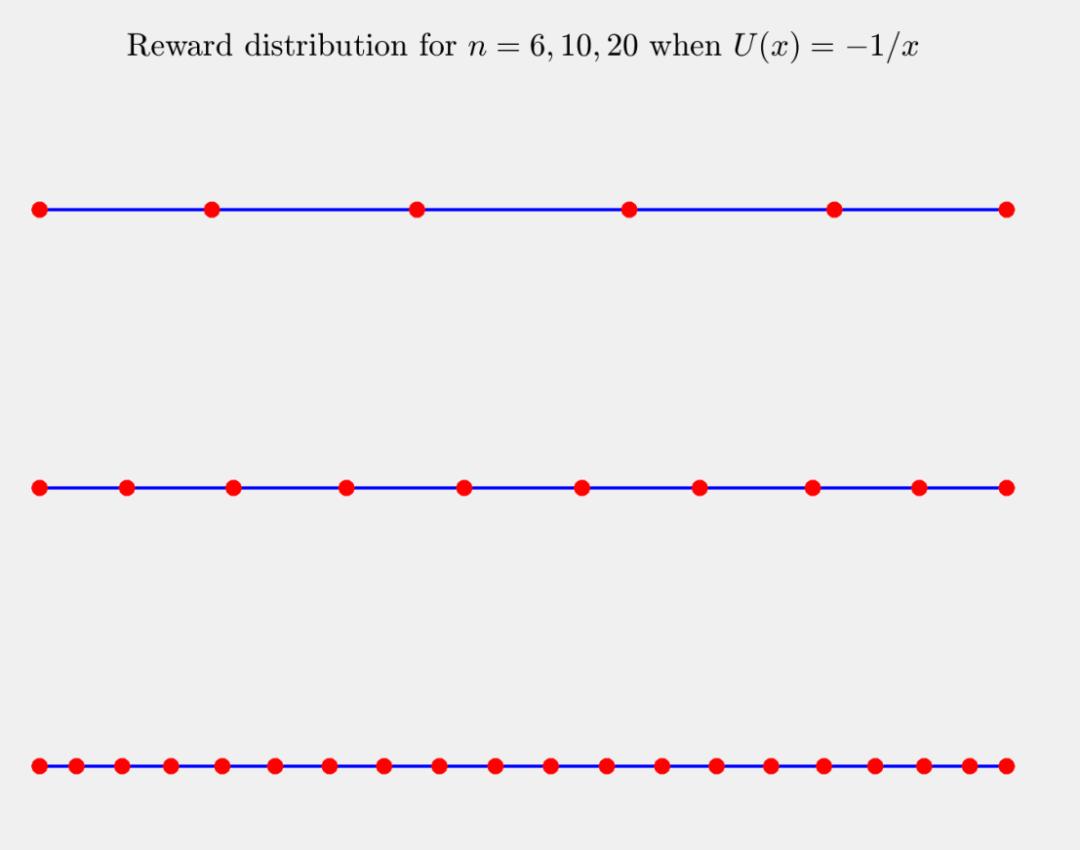
Figure 3 奖励分布
然而,作者发现这种基于排名的方式存在一个问题,那就是 “奖励坍缩”。这是由于排名的方式无法准确地反映出不同提示下的奖励分布差异。举个例子,对于开放性的提示,比如 “写一个中国男足勇夺世界杯的故事”, 应该有一个连续范围的奖励,因为故事可以有许多可能。但对于事实性的提示,比如 “中国男足在世界杯进过球吗”, 回应应该只有两种情况:进过或者没进过。因此,不同类型的提示应该有不同的奖励分布。但在训练的最后阶段,我们发现所有提示的奖励分布都变得完全相同,这就是 “奖励坍缩”。我们可以将效用函数理解为一种 “排斥力”, 奖励坍缩本质上是因为对不同对提示用了同一个 “力”。为了避免奖励坍缩,必须使用不同的力,也就是不同的效用函数。
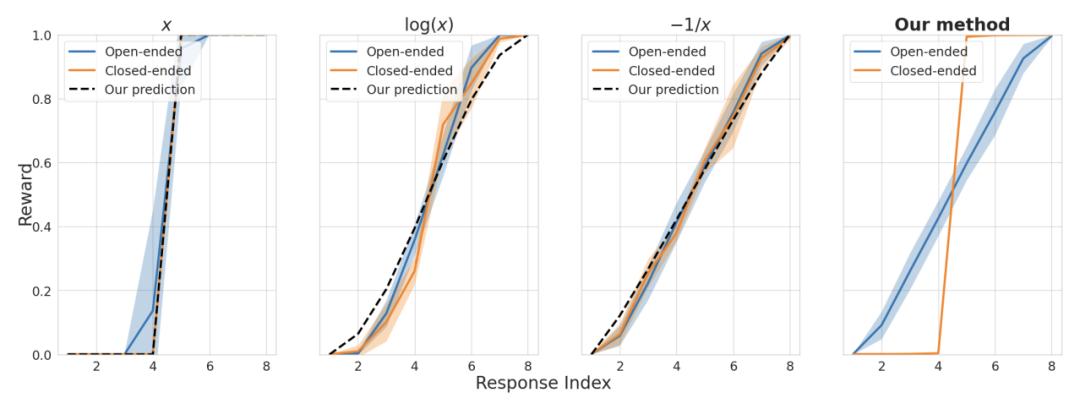
Figure 4 奖励坍缩的示例
上图展示了奖励坍缩的现象。对于开放性的提示,应该有一个大致均匀的奖励分布,而确定性的提示应该只有高分和低分两种 (两点分布)。然而,当使用固定的效用函数进行训练时 (见上图的前三张图), 这两种类型的提示都会导致相似的奖励分布,这是我们不希望看到的。相反,当使用我们提出的基于提示 (Prompt-Aware) 的效用函数时 (见上图的最后一张图), 两种类型的提示就会显示出不同的奖励分布。
奖励坍缩的数学原理
在 over-parameterized 的假设下,对于每个输入的提示,我们考虑的优化问题会成为
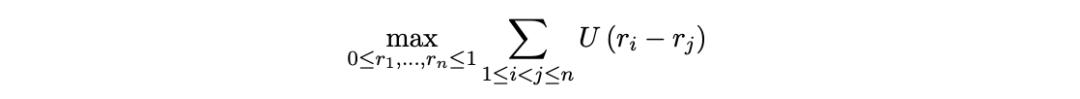
Figure 5 简化的优化问题
其中的 U 是效用函数。当 U 是凹函数的情况下,这个问题是一个凸优化问题。
这个优化问题可以理解为尽可能在保持不同回应好坏次序的情况下最大化不同回应的奖励之间的距离。可以看出,这个优化问题与我们训练奖励模型里输入提示并没有任何关系,因此对不同输入提示得到的奖励将没有差异,只和我们选用的效用函数 U 有关。
训练奖励模型和数学、物理的联系
上面考虑的优化问题也有物理上的解释。我们可以考虑有 n 个点在一个线段上。保持次序并且最大化距离可以理解成每两个点之间都有排斥力。我们想知道的是这里的稳态分布。从物理上来说,-U 可以理解成势能函数,这个求和的相反数就可以理解为整个体系中的势能总和。因此,我们实际上就是想要势能最小的分布。
更具体的,如果 U =1/x, 那么这个问题就等价于在一个线段上有若干个电子,求它们的稳态分布。这就是物理中的麦克斯韦问题或汤姆孙问题。
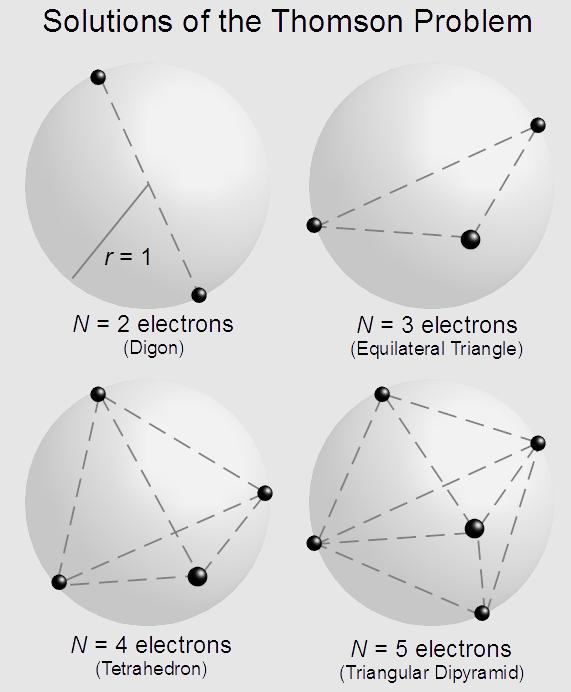
Figure 6 球面上的汤姆孙问题
如果 U = -log x 并且将奖励换成高维的向量,这就变成了 Steve Smale 在 1998 年提出的十八个问题中的第七个 (1998 年,时任国际数学联盟副主席、俄国数学家弗拉基米尔・阿诺尔德当时参照 20 世纪初希尔伯特的 23 个问题而向世界上的主要数学家征集面向 21 世纪的数学问题,斯梅尔便是在此背景下提出了斯梅尔问题,作为对阿诺尔德的答复)。

Figure 7 Smale 第七问题
这个问题至今仍未被解决。所幸我们假设奖励是一维的,这个问题就成为了一个可解的凸优化问题。
奖励分布的数学理论
作者考虑了当 n 趋于无穷时的情况并建立了收敛定理:即在假设 U 是强凹,递增有界的情况下,奖励会收敛到唯一的分布。他们还发现这个分布可以通过解一个在概率分布上的优化问题得到。

Figure 8 收敛定理
一族例子是 U = x^a, 0
在 U = -x^{-a}, 0
对于 U = x, 最终的极限分布是两点分布。对于 U =-1/x, 最终的极限分布是均匀分布。这也对应于当电子足够多的时候,线段上的电子的稳态分布会趋向于均匀分布。
值得一提的是,作者还证明了在 U 满足一定的性质的情况下 (例如 log sigmoid 函数), 奖励的极限分布以正概率等于 0, 1。
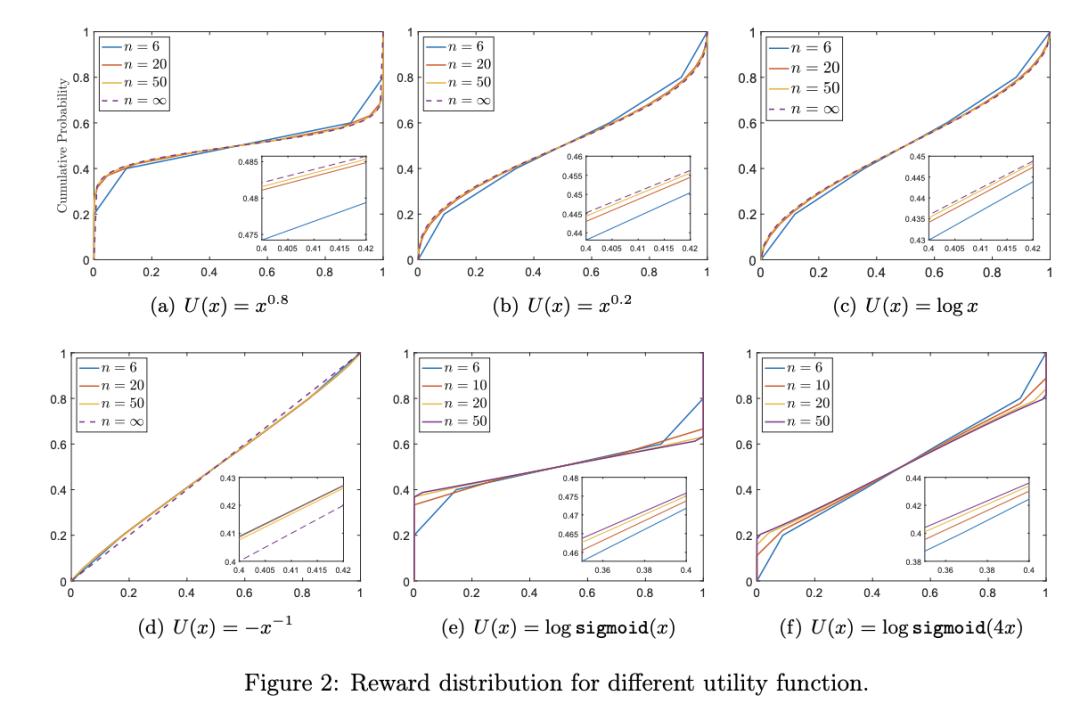
Figure 9 不同效用函数下的奖励分布
基于提示的效用函数
既然固定效用函数会有奖励坍缩的存在,作者提出根据不同提示选择不同的 U。先考虑 x 和 - 1/x 上。U = x 时奖励会收敛到两点分布,对应于确定性提示,U=-1/x 时奖励会收敛到均匀分布,对应于开放性提示。我们可以根据提示的不同,选择不同的效用函数。
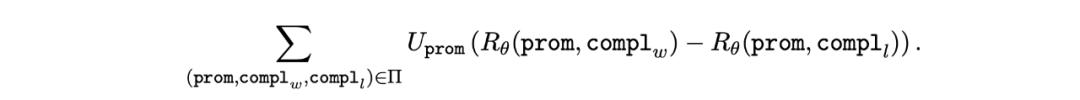
如果提示的开放程度可以量化,我们也可以根据开放程度选择 U = x^a, 0
实验
因为现有的开源数据集相对有限,作者策划了自己的数据集。他们关注的是一个简单的特征 —— 答案的长度 —— 作为真实的奖励。
作者从 LongForm 数据集中选取了一部分问题,为了模拟开放性和确定性提示,根据两种不同的长度分布截断了原始答案,生成了每个问题的八个回答。每个问题都被随机分配为开放性或确定性提示。通过这个过程,他们构建了一个包括 8192 个训练提示和 16 个测试提示的数据集。实验将重点研究以下几种效用函数:x, log x, -1/x, 和 Prompt-Aware U。
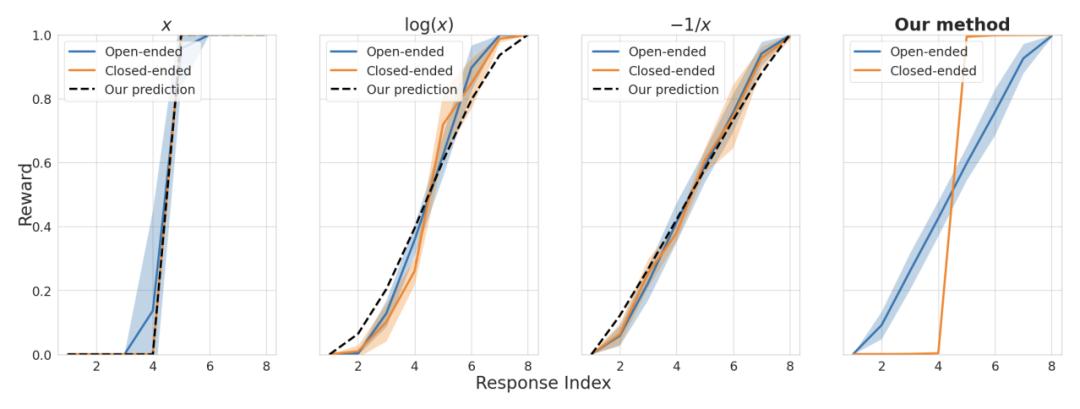
Figure 10 实验中的奖励坍缩情况
实验结果很好地验证了奖励坍缩现象的存在以及文中对奖励分布的理论刻画。固定效用函数后,对不同的输入提示,奖励都会收敛到同一个分布。特别地,采用 x 作为效用函数会导致两极分化的奖励分布,而采用 -1/x 作为效用函数则会导致均匀的奖励分布。
使用基于提示 (Prompt-Aware) 的效用函数可以在训练和测试数据集上有效防止奖励坍缩。这种策略对于开放性提示产生更均匀的奖励分布,而对于确定性提示则推动了更两极分化的奖励分布。
对实际的启发
需要指出的是,在实际训练奖励模型时,奖励坍缩现象并没有那么明显,因为实际训练通常会选择 early stop (甚至一个 epoch) 来避免过拟合。这其实也暗中减小了奖励坍缩的影响。为了解决奖励坍缩的问题,这篇论文中提出了一种新的优化方案。作者建议在训练奖励模型时,根据输入提示的特性选择不同的效用函数,使得奖励分布可以在广泛的范围内变化,或者密集地集中在某一点,取决于提示是开放性的还是确定性的。他们的初步实验结果已经表明,这种基于提示的方法可以显著减轻奖励坍缩的现象。
在未来还有很多可以考虑的研究方向。一个很重要的问题就是如何定量判断一个提示的开放性程度,如果可以定量判断提示的开放性程度,我们就可以选择对应的效用函数。另一个问题是能不能通过一个奖励分布反推出能得到这个奖励分布的效用函数。这对于我们选择更多样的效用函数有很重大的意义。
这篇文章中的理论研究不仅从优化角度揭示了大型语言模型在处理人类反馈时会遇到的问题,也提供了一个简单的解决方案,这将对未来的人机对齐研究带来启迪。随着对这个现象的理解不断深入研究,将会有更多的策略和方法出现,以进一步改善大型语言模型的性能。
© THE END
转载请联系本公众号获得授权
投稿或寻求报道:content@jiqizhixin.com
原标题:《大模型也有好玩的数学 从麦克斯韦的最低势能问题到人机对齐》
本文为澎湃号作者或机构在澎湃新闻上传并发布,仅代表该作者或机构观点,不代表澎湃新闻的观点或立场,澎湃新闻仅提供信息发布平台。申请澎湃号请用电脑访问http://renzheng.thepaper.cn。





- 报料热线: 021-962866
- 报料邮箱: news@thepaper.cn
互联网新闻信息服务许可证:31120170006
增值电信业务经营许可证:沪B2-2017116
© 2014-2025 上海东方报业有限公司




