- +1
学术丨张十庆:基于栱心格线的斗栱构成:中日斗栱尺度设计的比较分析
斗栱尺度设计方法的探讨,一直是建筑技术史研究关注的重点。斗栱尺度关系的特色很大程度上基于其独特的斗栱构成关系,本文以斗栱构成关系这一线索,探讨唐宋斗栱尺度设计的方法和特色,并与日本唐样斗栱作比较分析。
基于栱心格线的斗栱构成:
中日斗栱尺度设计的比较分析
Aligning a Block on a Bracket: A Clue to the Measurement Design of Dougong in Chinese and Japanese Architecture
张十庆
ZHANG Shiqing
斗栱尺度设计方法的探讨,一直是建筑技术史研究关注的重点。以往学界关于唐宋斗栱的研究基本是以宋《营造法式》材份制度为线索展开的。就斗栱构造的视角而言,斗栱尺度关系的特色很大程度上基于其独特的斗栱构成关系,且斗栱构成关系有可能与其尺度设计方法相关联。本文基于斗栱构成关系这一线索,探讨唐宋斗栱尺度设计的方法和特色,并与日本唐样斗栱作比较分析。
1 斗栱构成的基本格线关系
斗栱构成上,由斗栱分件拼合的需要,生成相应的定位格线,其间隐含着基于构件拼合关系所生成的控制性比例关系。也就是说,上下铺叠、前后出跳、左右伸出的斗栱构成,以定位格线的形式显示控制性比例关系的存在及特点。
分析斗栱构成的规律和特点,其重要的控制性比例关系有二:一是竖向的跳高,一是横向的跳距,且在竖向跳高与横向跳距的两个向度上,各有不同的表现形式。竖向的跳高取材栔分位,以材栔格线的形式控制跳高的比例关系;横向的跳距取栱心分位,以栱心格线的形式控制跳距的比例关系。跳高、跳距尺寸的简洁和取整,唐宋以后愈显重要(图1)。
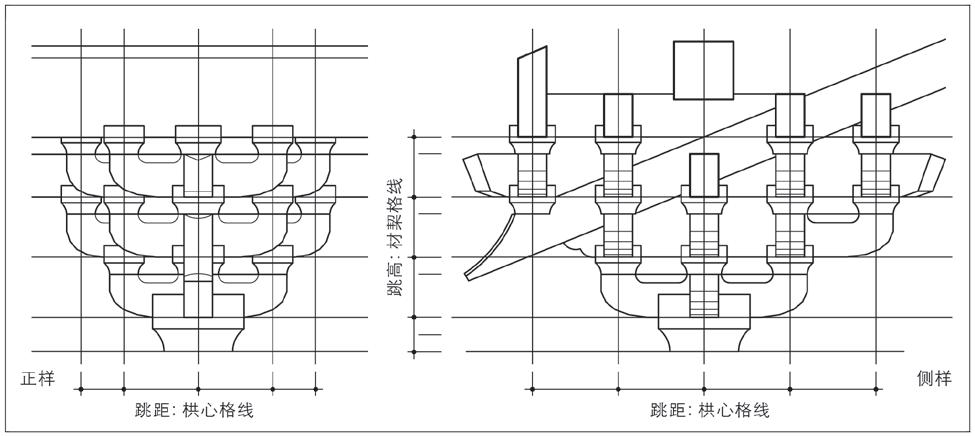
图1 唐宋斗栱构成的定位格线关系:竖向跳高与横向跳距
斗栱构成的两个向度中,跳高以材、栔计,其值为一材一栔,合一个足材;跳距分作华栱跳距与横栱跳距两种。《营造法式》规定重栱计心造华栱跳距以份计,其值为2材、30份;且根据分析其横栱跳距的原型也是以2材、30份为定式的。
竖向的跳高与横向的跳距,是斗栱构成上的两个基本定位格线,二者决定斗栱构成的基本比例关系。《营造法式》重栱计心造制度,在斗栱构成上以足材的跳高与二材的跳距,形成一对基于材的定位格线,且栱心跳距成为横向尺度计量的一个基本单位。
斗栱构成的双向格线关系中,横向尺度构成的关键在于栱长,而栱长的控制分位在于栱之心长跳距。栱之心长的意义在于栱斗拼合关系中的定位,而栱之实长则是栱之心长与斗底尺寸的复合。因此,栱之心长的设定,既是构造设计,也是尺度设计,栱之心长跳距在斗栱构成上具有重要的意义。
在横向尺度设计上,栱心跳距的意义在于小斗配置与栱长设计,并由此演化出相应的斗栱尺度设计方法和特色,成为唐宋斗栱尺度设计的一个重要表现。
要之,唐宋斗栱尺度构成基于跳高、跳距的双向格线关系,并向材栔模数的方向演进。实际上,唐宋斗栱构成上跳高与跳距这两个基本格线关系,是此后所有斗栱尺度关系筹划的原点与基石,包括日本中世(1185—1573)唐样斗栱尺度设计。
2 唐宋斗栱尺度设计的栱心格线法
2.1 基于栱心格线的尺度组织与筹划
基于栱心格线的尺度组织与筹划,是唐宋斗栱尺度设计的一个基本方法。从尺度设计的角度而言,基于栱心格线的小斗配置与栱长设计及其细化和演进,表现和推进了唐宋斗栱尺度设计方法及其模数化的发展。
斗栱构成上,栱心跳距的作用表现为横向尺度关系的组织筹划。在构成关系上,栱心跳距的构成可分解为:栱心跳距=斗间+斗长,斗间与斗长成为栱心跳距构成的两个要素。
所谓“斗间”,指斗栱立面上小斗与小斗之间的空当,“斗长”则指小斗长。而建立斗间与斗长两要素之间的关联性,是栱心格线设计法的关键。其方法是权衡斗间与斗长的比例关系,也就是建立二者间的简洁比例关系,从而进一步细分栱心跳距格线,并以细分单位作为权衡斗栱横向尺度的基准。
建立斗间与斗长的简洁比例关系,是细化栱心跳距最直观和直接的方法。唐宋时期小斗的斗长单一,为这一比例关系的建立提供了前提和条件。
早期斗栱的小斗斗型,相应于不同的施用位置,小斗尺寸几乎没有什么变化和差异,小斗的单一斗型成为显著的特征。尤其是在斗栱立面上,所有可见小斗,皆为大小相同的单槽小斗形式。因此,早期斗栱立面构成,表现为基于单一斗型的小斗配置。
以早期木构遗存较多的晋东南地区为例,金代以前的遗构大多为单一斗型做法。以盛唐建筑为祖型的日本奈良、平安时代建筑,其小斗亦为早期的单一斗型做法。而江南约在唐末五代出现小斗的分型,并成为影响北宋官式斗栱制度的一个重要因素,北宋末的《营造法式》实现了小斗分型的制度化。
要之,斗栱尺度设计上,栱心格线细化的意义在于建立斗间与斗长的简洁比例关系,即以栱心格线细分的“斗间”为细分基准,以之精细组织和筹划斗栱的横向尺度关系。现存唐宋遗构以及传承宋技术的日本中世唐样建筑,都不同程度地反映了这一技术特色。而至宋末《营造法式》小斗分型的制度化,使得这一相对简单、直观的设计方法,失去了存在的前提和条件,分化的斗型打乱了原先均等的格线关系,基于斗间与斗长比例关系的尺度设计方法不复存在。
2.2 栱心跳距的细化与细分基准的建立
斗栱设计技术上,栱心跳距细化的目的在于细分基准的建立,且这一进程是逐渐推进的。从偷心到计心的演进,斗栱构成上跳高与跳距(尤其是跳距)的变化是相当显著的。陈彤根据早期遗构佛光寺东大殿、独乐寺观音阁的分析,指出早期偷心造斗栱跳距格线的如下特色和规律:
七铺作隔跳偷心斗栱,侧样以每二跳计心位置的跳距心长之半为格线,正样与侧样对应,同样以横栱二跳的跳距心长之半为格线,且正侧样跳距格线尺寸对应相等(图2)。
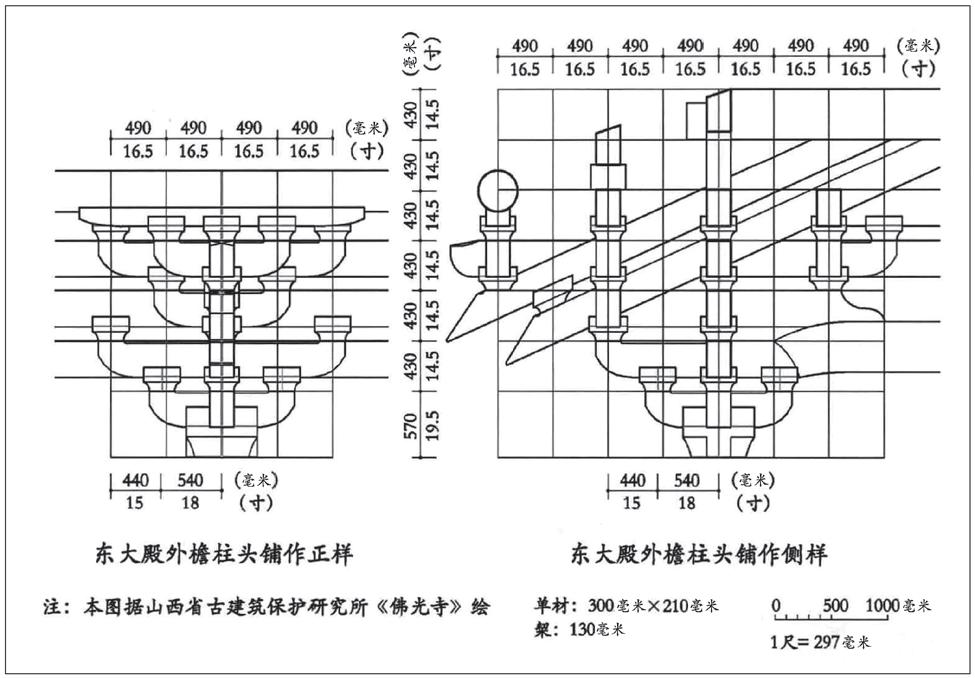
图2 佛光寺东大殿偷心造斗栱的尺度构成
上述早期二构偷心造斗栱构成上正侧两向的一大跳心长对应相等,且以一大跳心长之半为控制格线。也就是说,斗栱的横向尺度构成,是以栱心跳距格线为基准和目标的。
另一方面,根据唐辽遗构的分析隐约可见,其时斗栱横向尺度筹划的意识及方法已经形成,栱心格线有了进一步的细化,其方法是建立斗间与斗长的简洁比例关系,由此形成基于栱心跳距分数的格线关系。如佛光寺东大殿斗栱正样横向尺度的组织与筹划,应是基于栱心跳距三等分的细分格线关系,斗间与斗长呈1∶2的简洁比例关系,在斗栱立面尺度权衡上,表现为1/2斗长格线的形式(图3)。辽构应县木塔的斗栱尺度构成,也见有与佛光寺东大殿斗栱相同或类似的形式,其斗栱正样的横向尺度组织与筹划,有可能也是基于1/2斗长的格线关系(图4)。时代相近的辽构华严寺薄伽教藏殿的斗栱尺度构成,也具有同样的特色(图5)。
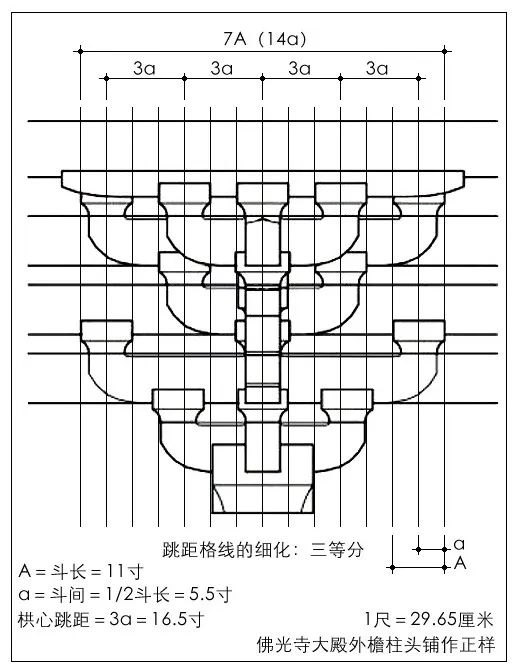
图3 佛光寺东大殿斗栱立面横向尺度关系的组织与筹划
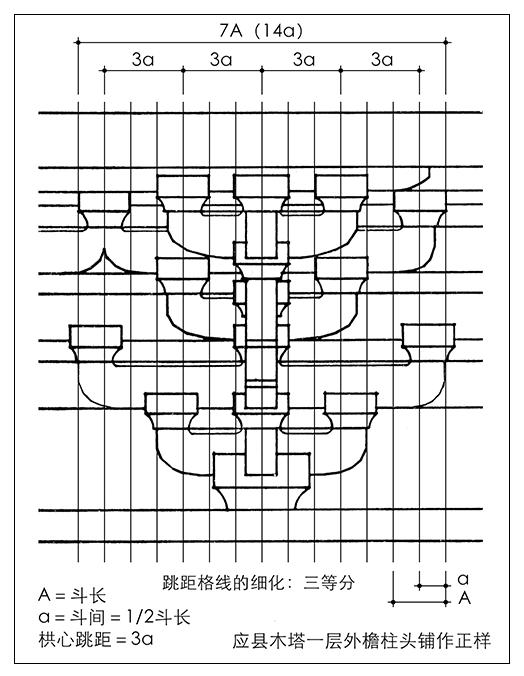
图4 应县木塔斗栱立面横向尺度关系的组织与筹划
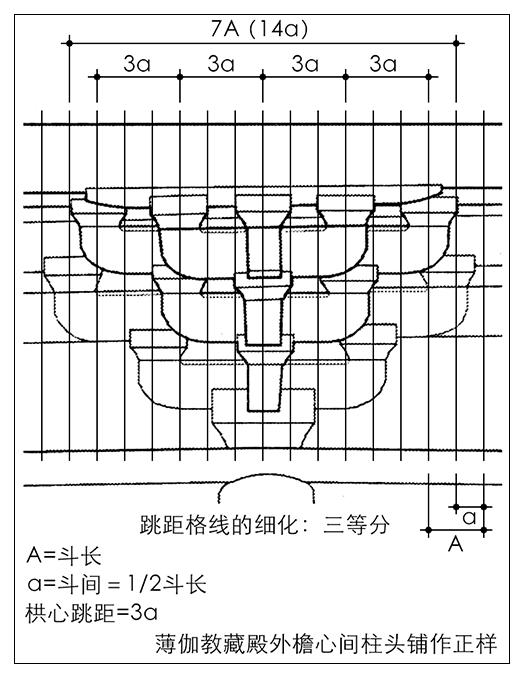
图5 华严寺薄伽教藏殿斗栱立面的尺度构成
唐辽遗构上斗栱横向尺度的组织与筹划,表现出基于栱心跳距分数的方法和特色,即通过建立斗间与斗长的简洁比例关系,以小斗长的简单分数的格线形式,权衡斗栱的横向尺度关系。除上述唐辽遗构的1/2斗长格线关系外,1/3斗长格线关系在辽宋遗构上应也存在,如镇国寺万佛殿斗栱横向尺度的组织与筹划,应是基于栱心跳距四等分的细分格线关系,斗间与斗长呈1∶3的简洁比例关系,在斗栱立面尺度权衡上,表现为1/3斗长格线的形式(图6)。
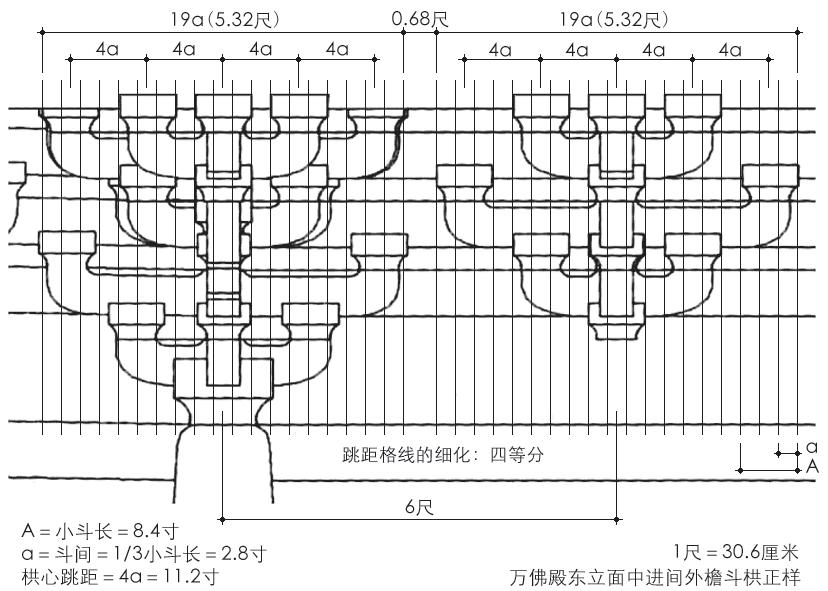
图6 镇国寺万佛殿斗栱立面的尺度构成
辽构中的另一例独乐寺观音阁,其基于栱心跳距格线的斗栱构成关系,与镇国寺万佛殿相同。此外,根据实测尺寸及图示分析,敦煌第431窟宋初窟檐斗栱的横向尺度关系,应也存在基于细分栱心格线的构成关系(图7)。
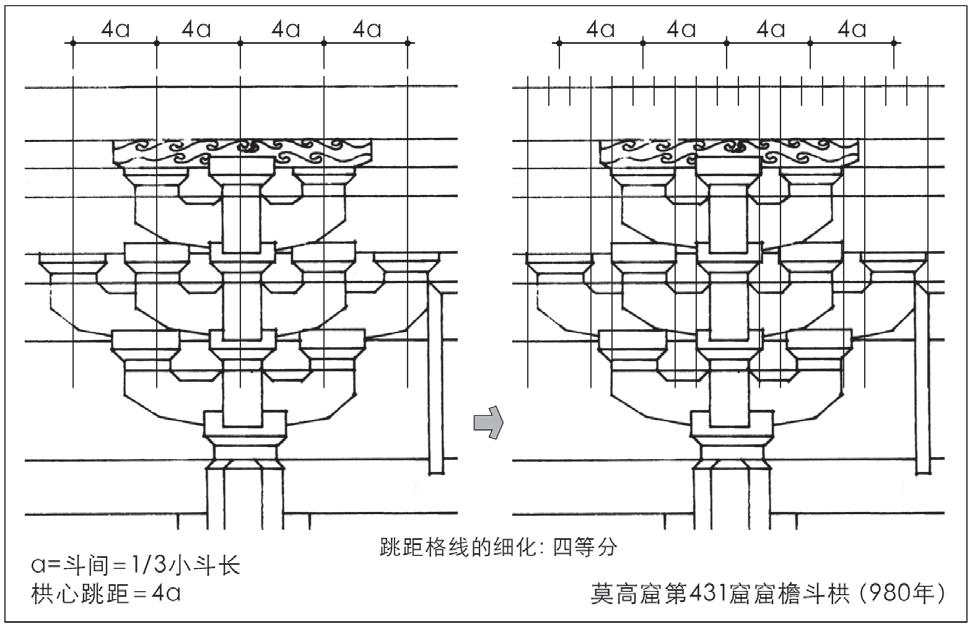
图7 敦煌宋窟斗栱立面横向尺度关系的组织与筹划
上述以栱心跳距分数的斗间作为细分基准,精细筹划斗栱横向尺度的方法,多见于早期遗构,也就是在补间铺作多朵尚未出现、慢栱长未相应缩减的时代,其表现尤为典型。以上从唐、五代到北宋初的几个遗构实例,斗栱立面构成显示出一致的规律性,诸例斗栱立面横向尺度的组织与筹划,实质上都是基于栱心跳距格线而展开和变化的。
有意味的是,上述唐宋斗栱构成特色,在此后的日本唐样建筑中也有典型的表现和发挥。日本中世唐样斗栱立面构成的基准方格模式,也是由唐宋斗栱的基本格线关系细化、演变而来。基于栱心跳距及其细化的斗间格线,同样是传承宋技术的中世唐样斗栱尺度设计的基本方法。
2.3 基于跳高与跳距的双向格线关系
材栔比例关系及其变化,反映了不同时期斗栱比例关系的变迁和特点。考察现存遗构的材栔比例关系,早期栔高较大,并呈现逐渐减小的趋势。晚唐及辽宋前期的早期遗构,栔高大多接近或等于材广之半,即栔材比为1∶2。栔为材之半,应是这一时期材栔比例关系的一个重要形式。而至宋末《营造法式》时期,栔高已显著减小,栔材比定型为2∶5,栔为材的0.4倍。
然而,栔取材之半也只是辽宋时期的一个阶段形态,唐代前期的栔高有可能更大,日本奈良、平安时代遗构中保留了这一材栔比例的早期形态,有如下两个特点:一是材截面形状偏方,材之广厚比在1.2(6∶5)左右;二是栔材比值较大,多在0.8(4∶5)上下,栔远大于材之半,接近甚至大于材厚。
概括材栔比例关系的演变趋势,栔材比大致由隋唐的4∶5,演变为宋以后的2∶5。而栔取材之半(1∶2)这一简洁比例形式,作为中间形态在辽宋前期是一个较稳定的比例关系,并在日本中世以后为唐样建筑所传承。
材栔比例作为斗栱构成的基本比例关系,反映在斗栱的竖向尺度关系上。辽宋遗构所表现的早期栔材1∶2的简洁比例关系,在竖向尺度上形成基于1/2材的均等材栔格线。
唐宋斗栱构成上,横向的栱心格线与竖向的材栔格线,成为斗栱尺度设计的基本格线关系。其方法是以两向格线的细分基准,权衡、筹划斗栱横向与竖向的尺度关系。以辽构独乐寺观音阁为例,观音阁斗栱的尺度设计,以跳距四等分的斗间(0.35尺)和跳高三等分的1/2材(0.425尺),分别作为细分基准,权衡、筹划斗栱横向和竖向的尺度关系(图8)。
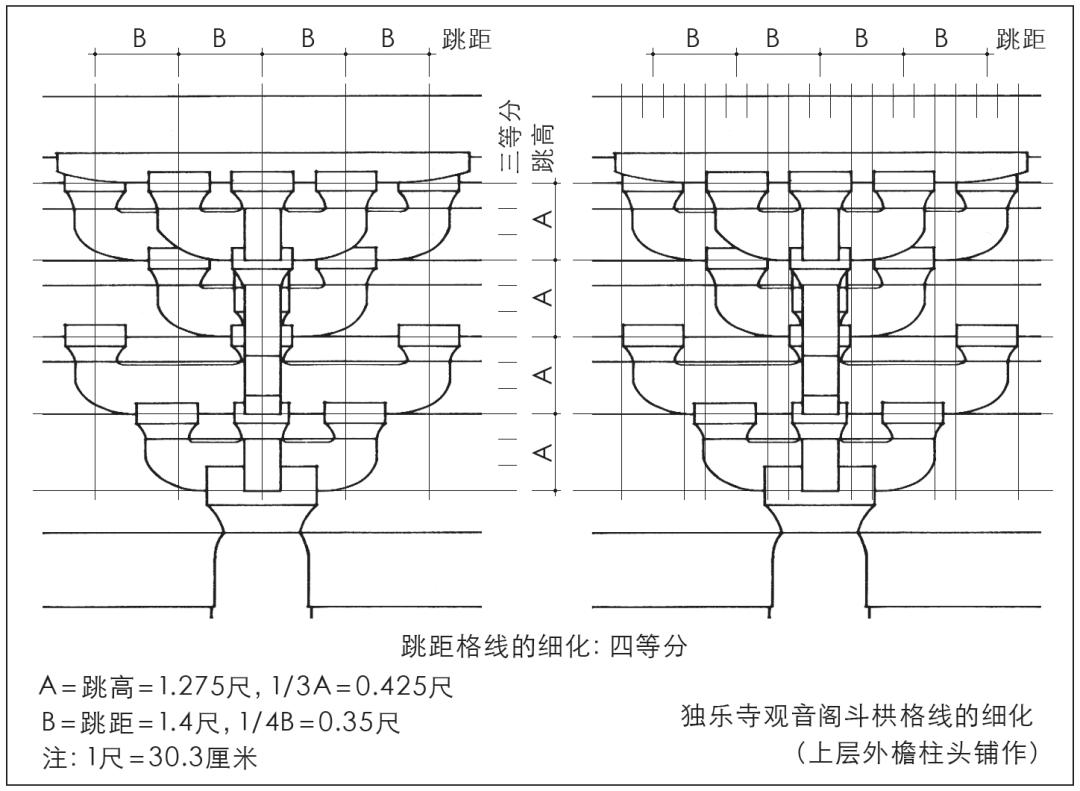
图8 独乐寺观音阁斗栱立面的尺度构成
相同及类似的斗栱尺度设计方法,再以日本实例作对照和比较。
深受宋技术影响的日本中世和样鑁阿寺本堂,其斗栱尺度设计意图与方法,采取的应是宋式斗栱格线法,即以跳高、跳距格线权衡和设定斗栱的尺度关系,并以跳高0.8尺、跳距1尺为本堂斗栱构成的基本尺寸(图9)。本堂斗栱的尺度构成,在宋式斗栱格线关系的基础上,作进一步的细化,进而建立斗栱立面方格模式,表现了本堂斗栱尺度设计的意匠和方法(图10)。
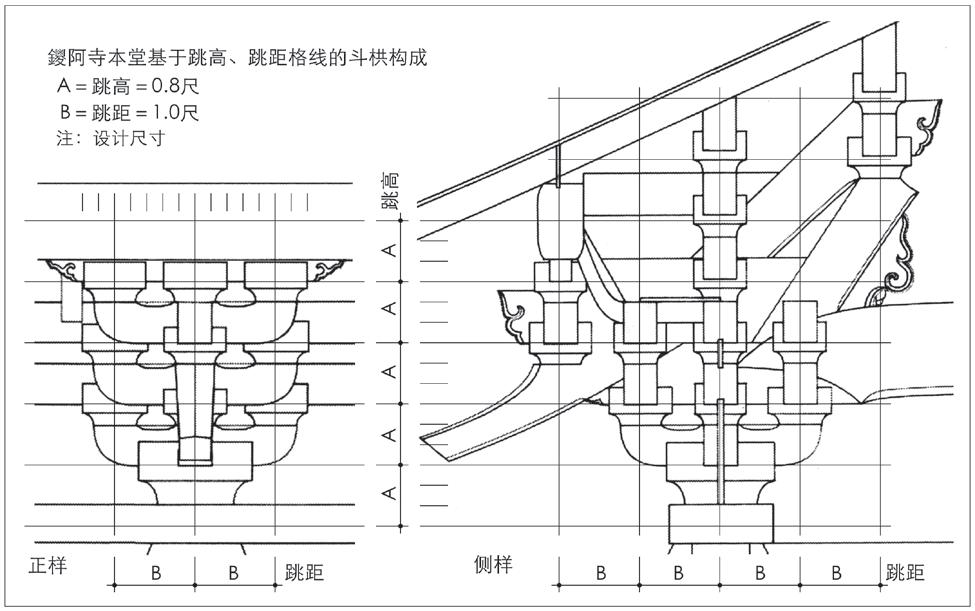
图9 鑁阿寺本堂基于跳高、跳距格线的斗栱构成
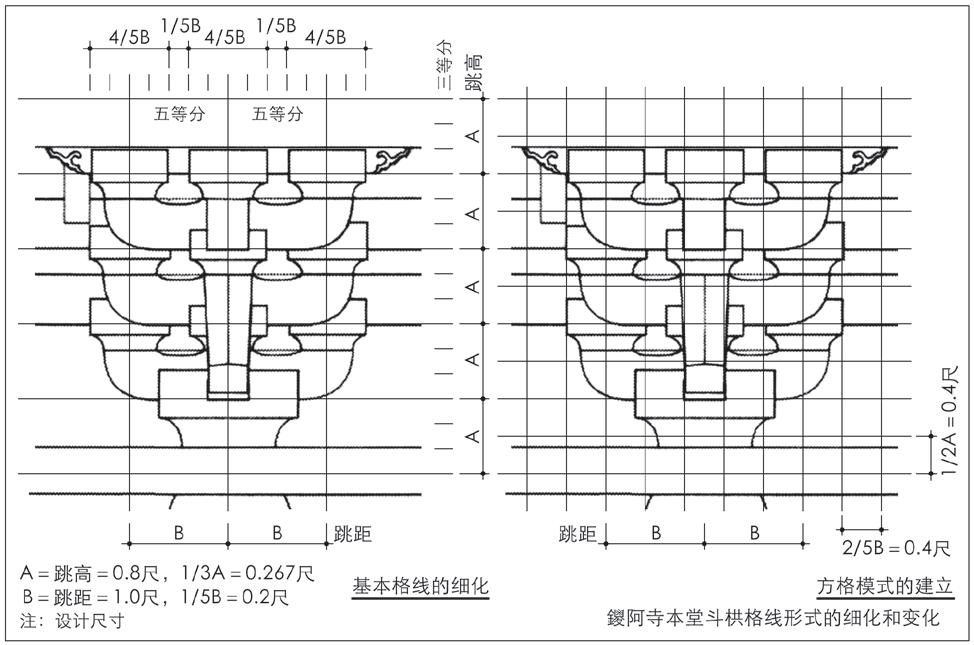
图10 鑁阿寺本堂斗栱格线形式的细化和变化
鑁阿寺本堂斗栱尺度设计方法如下:
横向尺度上,以跳距B细分作五份,每份为0.2尺,作为权衡横向尺度关系的细分基准:
小斗长=4/5B=0.8尺,斗间=1/5B=0.2尺,斗栱全长=14/5B=2.8尺;
竖向尺度上,以跳高A细分作三份,每份0.267尺,以之权衡竖向尺度关系:
材广=2/3A=0.533尺,栔高=1/3A=0.267尺,斗栱总高=4A=3.2尺(栌斗底至橑檐枋下皮)。
本堂斗栱构成的特点在于立面方格模式的建立:以跳距的2/5为方格横向单位(0.4尺),以跳高的1/2为方格竖向单位(0.4尺),建立斗栱立面的基准方格模式,且这一特色表现了与唐样斗栱设计技术的关联性。和样羽黑山五重塔的斗栱尺度设计,同样也表现了基于材栔的斗栱方格模式(图11)。
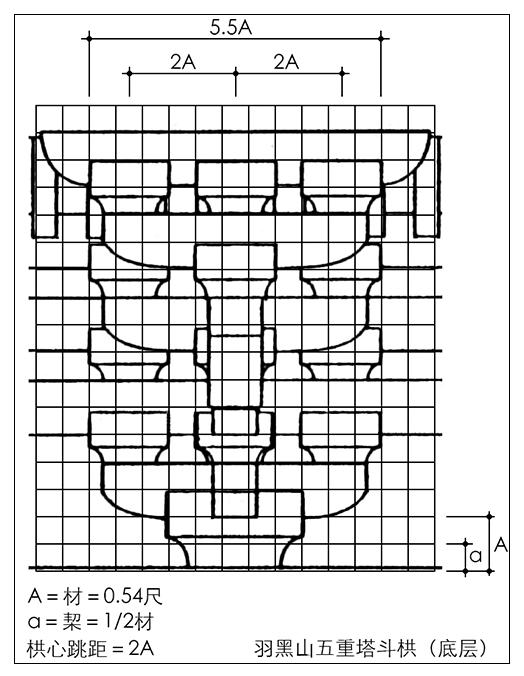
图11 羽黑山五重塔基于材栔的斗栱立面构成
比较唐样高仓寺观音堂的斗栱尺度设计,其斗栱构成基于跳高、跳距的双向格线关系,以跳高4.44寸细分作三份,跳距5.92寸细分作四份,以其一份1.48寸为细分基准,权衡和设定斗栱尺度关系(图12)。
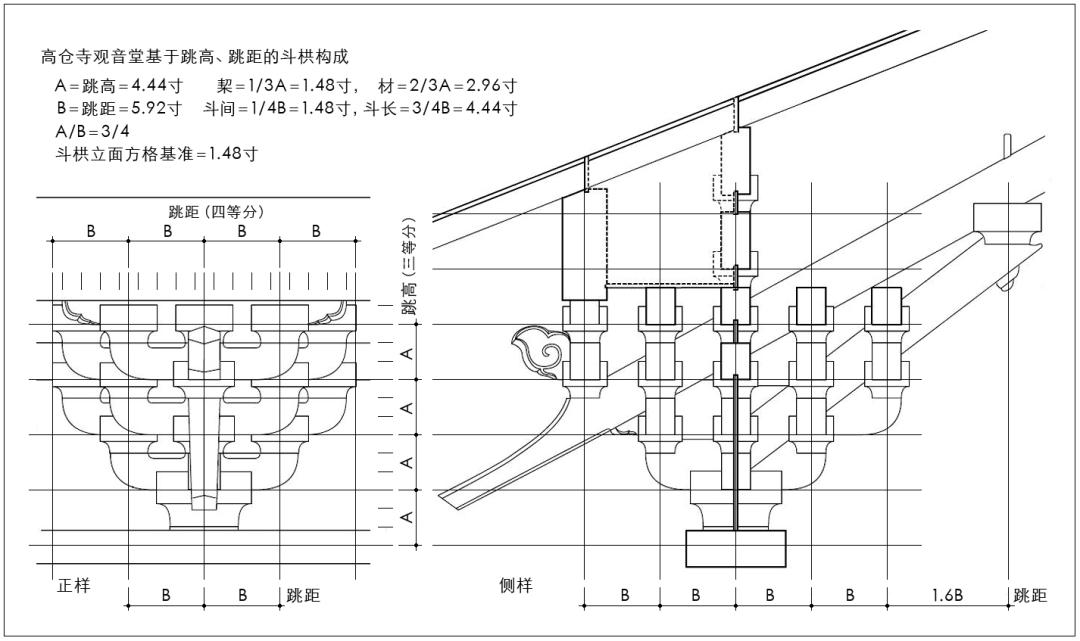
图12 高仓寺观音堂基于跳高、跳距的斗栱构成
以上诸例斗栱尺度关系分析,显示了一致的斗栱尺度设计意匠和方法,且这一基于格线关系的设计方法,成为日本中世唐样斗栱尺度设计的一个重要特色。
3 日本唐样斗栱构成及其变化
3.1 基于栱心格线的斗栱尺度设计
唐宋以来斗栱技术的演变和发展,随南宋技术的传播而影响日本中世斗栱技术,尤其是以江南宋元建筑为祖型的中世唐样建筑。
以传承宋技术为特色的中世唐样建筑,在斗栱技术上的进步最为显著,并表现在斗栱的比例关系及尺度设计上。唐样斗栱构成上追求规整化的背后隐含着特定的设计意识和方法。唐样斗栱立面尺度的有序组织和筹划,正是以其斗型与栱型的简洁和规整为基本条件的。小斗尺寸的统一与栱长构成的规整,对于唐样斗栱尺度设计有着重要的意义。
以宋式为祖型的唐样斗栱,在尺度构成和比例关系上尤为着力,并基于宋式斗栱构成的基本格线关系,形成唐样斗栱的尺度权衡方式,其中最具代表性的是斗栱立面构成的基准格线法。
基于栱心格线的斗栱横向尺度筹划,同样是唐样斗栱尺度设计的一个基本方法,而其较唐宋斗栱设计技术的进步,则表现为尺度构成的模数化。其方法是以材为模数基准,建立材与斗间、斗长的简洁比例关系,相应形成基于材的横向格线关系。下文以中世唐样代表性建筑功山寺佛殿、不动院金堂二构为例。
唐样斗栱立面构成上,基于栱心格线的小斗配置主要呈两种形式:一是斗畔相接型,一是斗畔相错型。两型以斗栱正立面上长、短栱端小斗的斗畔交接关系区分,前者斗畔相接,后者斗畔相错1/2格线,两型最终的差距反映在斗栱全长上。而功山寺佛殿与不动院金堂分别代表了上述两种小斗配置关系。
功山寺佛殿与不动院金堂二构斗栱为六铺作单杪双下昂,在横向尺度的权衡和筹划上,皆取栱心跳距四等分的形式,以其1份为细分基准,并等于1/2材,进而以之权衡和设定斗栱的横向尺度关系,即:斗间1份,小斗长3份,大斗长5份,栱心跳距4份。基于斗畔关系的不同,功山寺佛殿斗栱全长17份,合8.5材,不动院金堂斗栱全长16份,合8材(图13,图14)。
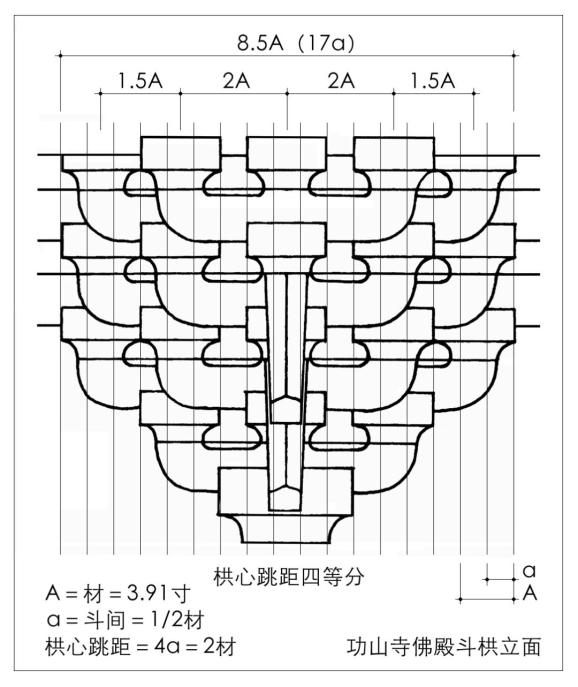
图13 功山寺佛殿斗栱的立面构成
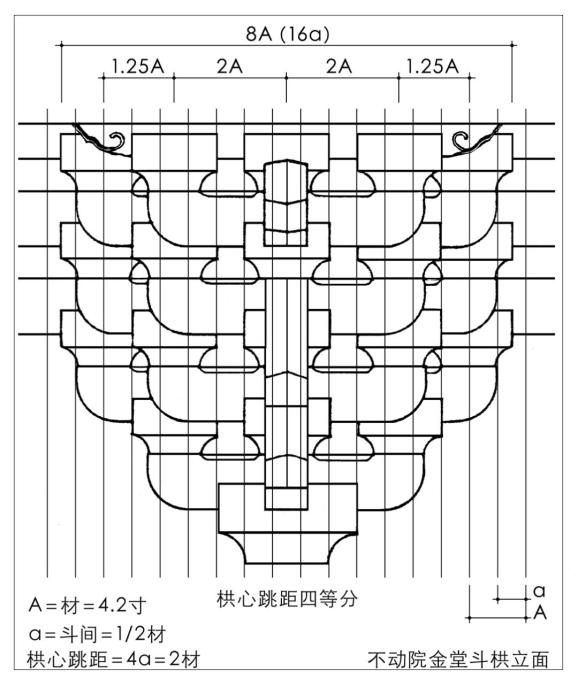
图14 不动院金堂斗栱的立面构成
上述唐样二构专注于横向尺度关系的单向格线形式,与前文讨论的唐辽遗构基于栱心格线的斗栱立面构成完全一致。
关于斗栱的实测尺寸,各种误差因素的干扰应是相当显著的。例如由于材料的干缩变形,小斗长的测值往往偏小,相应地,斗间的测值往往偏大,然二者测值之和,也就是栱心跳距,多不受材料变形的影响,可作为斗间、斗长实测值修正校验的一个依据。
3.2 唐样斗栱构成的材栔方格模式
相对于基于栱心格线的斗栱设计方法,斗栱构成上更规整、严格的格线关系,是斗栱立面的基准方格模式,也即基于跳距格线和跳高格线的细化所形成的两向格线关系。基准方格模式表现了唐样斗栱尺度设计精细化和程式化的特色。
尺度设计方法上,唐样斗栱立面方格模式,以简明、直观的基准格线,权衡和筹划斗栱立面的比例关系,进而生成尺度模数化的形式与方法,其模数基准有材栔、斗口和斗长三种形式的变化,显示了与中国本土技术的整体性和关联性。
唐样斗栱立面方格模式,尽管形式多样,但实质上都由唐宋斗栱基本格线的细化和改造而来。其方法是以跳高格线和跳距格线的若干等分为基准,建立斗栱立面构成的基准方格模式(图15)。与唐宋斗栱一样,在横向尺度的组织与筹划上,唐样斗栱也是基于栱心跳距而展开和变化的。其两向格线关系上,横向格线的两个基本尺寸单元为斗长、斗间,竖向格线的两个基本尺寸单元为材、栔(图16)。斗栱竖向尺度关系上,唐样六铺作斗栱以逐跳用华头子的方式,令交互斗逐跳归平,竖向斗栱构成吻合于统一的材栔格线关系。
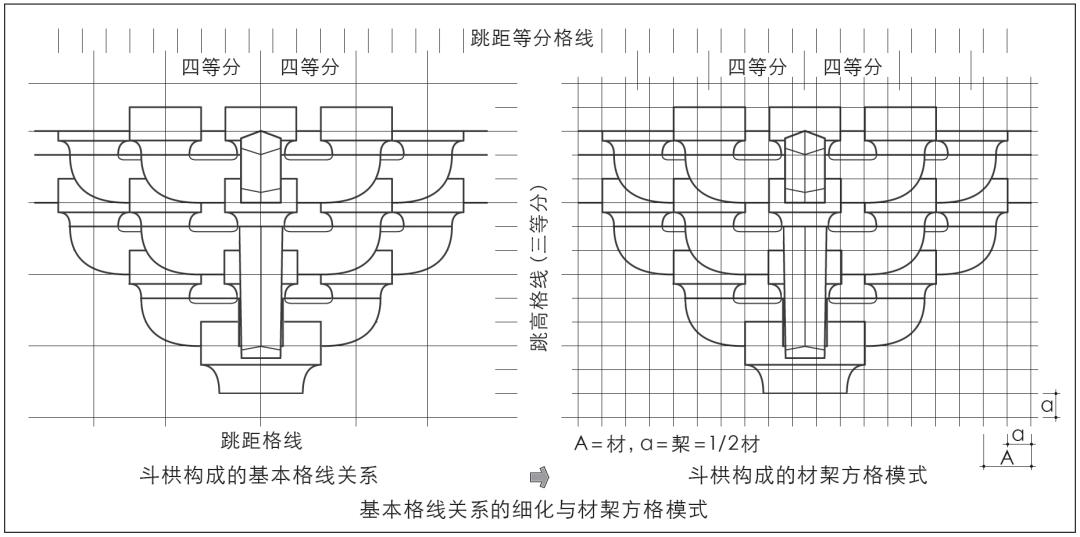
图15 基本格线关系的细化与材栔方格模式
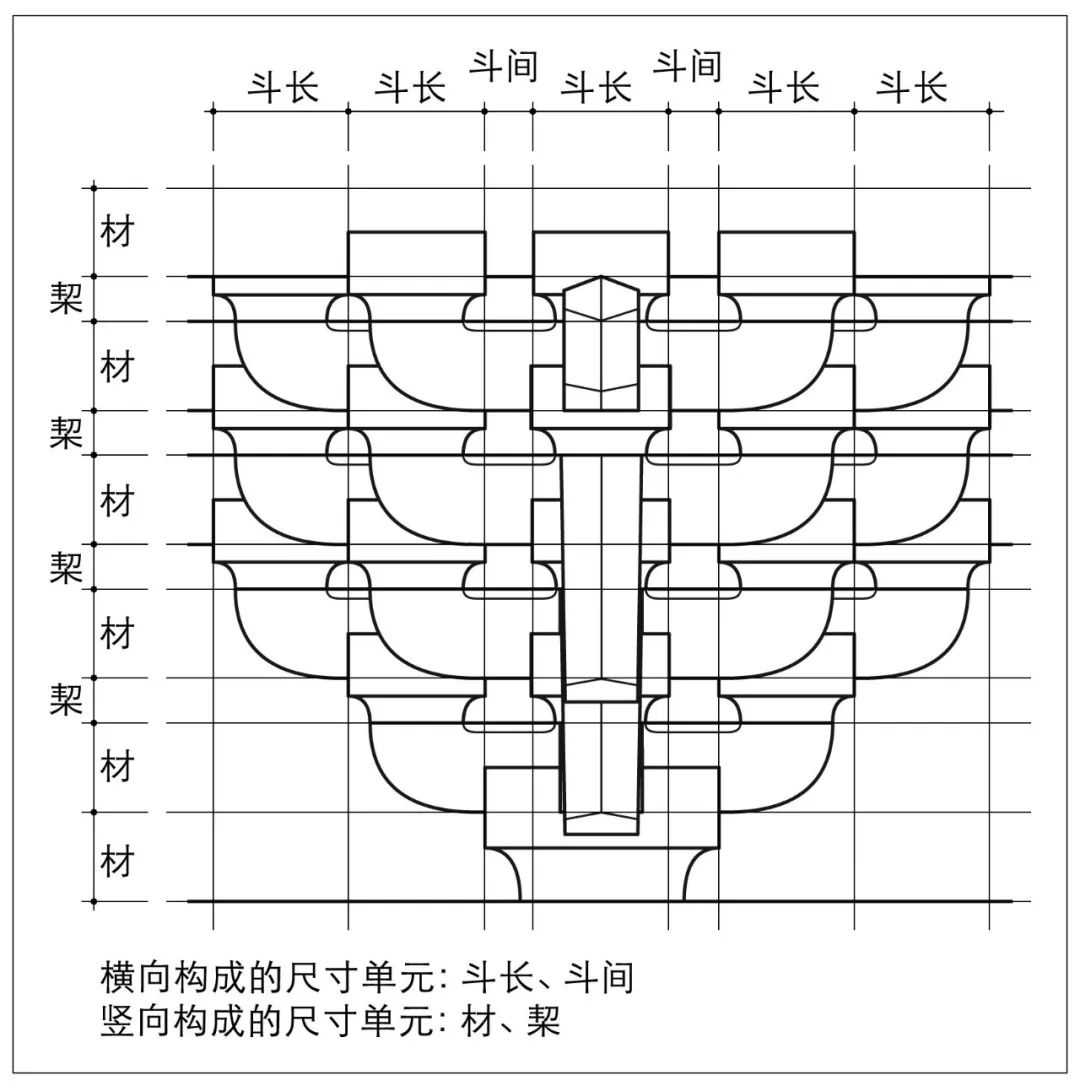
图16 唐样斗栱立面构成的基本格线形式
唐样斗栱立面的尺度构成与比例筹划,基于上述基本格线关系,作进一步的细化和推进,其方法是建立栔与材、斗间与斗长之间的简洁比例关系,也即栔取1/2材,斗间取1/2斗长或1/3斗长,相应地形成细化的斗栱立面方格模式。
在此基础上,若进一步规整化和比例化,如取竖向的栔与横向的斗间相等,则上述的斗栱立面方格则呈标准的正方格线形式,从而以一元基准的形式,权衡和设定斗栱立面尺度构成和比例关系。
唐样斗栱格线法的意义在于:简化斗栱立面构成关系,从而使得尺度构成和比例关系更加清晰、简明和直观。
唐样斗栱尺度关系多样复杂,统计分析表明:现存唐样遗构中严格吻合斗栱立面正方格线者,数量并不太多,部分唐样遗构虽非严格的正方格线形式,但多趋近这一模式,尤其是在斗栱横向尺度关系上,以斗间、斗长为基准的格线形式,成为唐样斗栱尺度设计上所注重和多用的形式。而在斗栱竖向尺度关系上,若取栔等于1/2材,其竖向格线可细化为均等的格线形式;若栔不等于1/2材,其竖向格线则呈材栔交替的格线形式。唐样斗栱尺度设计上,所注重的是横向尺度关系及其与朵当的关联性,而斗栱的竖向尺度关系,则是相对次要的局部比例设定。
横向尺度的组织与筹划,是唐样斗栱立面构成的重心所在。而横向尺度单元的斗间与斗长的比例关系,则成为唐样斗栱横向尺度筹划的关键。进而,通过将斗栱与朵当的尺度关系,转化为基于斗间、斗长的模数形式,从而建立斗栱、朵当及开间三者关联的整体尺度构成,而唐样斗栱立面构成,则成为其中的一个重要环节。
立面方格模式虽未必是中世唐样斗栱构成的唯一模式,但无疑是具有代表意义的一种重要形式。
唐样斗栱立面构成的基准方格模式的分型,以基准形式的不同和变化,可分作材栔方格模式、斗长方格模式与斗口方格模式三种类型,三型的基本模式如图17所示。
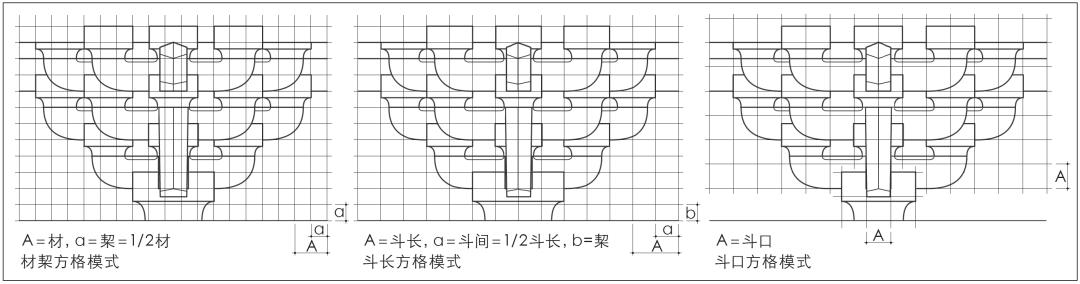
图17 中世唐样斗栱立面基准方格模式的分型
材栔方格模式是中世唐样斗栱立面方格模式中最基本的一种形式。其特点在于斗栱立面基准方格的两向边长尺寸,取材、栔尺寸为之,故称为材栔方格模式。材栔方格模式成立的基本条件是:
垂直方向:栔=1/2材
水平方向:斗间=栔=1/3小斗长
唐样斗栱立面的材栔方格模式,表现为以材、栔为基准的双向格线形式,栔为细分基准单位,栔、材之比为1∶2。
基于材栔方格模式,斗栱立面的构成关系如下(设栔为a,材为A):
栔=1/2A,小斗高=A,足材=大斗高=1.5A,大斗平欹高=A;
斗间=1/2A,小斗长=1.5A,大斗长=2.5A,短栱长=5A,长栱长=8A,栱心跳距=2A。
唐样材栔方格模式的实质在于斗栱构成的材栔模数关系。中世唐样遗构正福寺地藏堂的斗栱构成,是材栔方格模式的典型。
正福寺地藏堂上檐斗栱六铺作单杪双下昂,实测材广2.65寸,栔高1.35寸。综合斗栱、朵当的实测尺寸分析,其斗栱立面构成吻合于材栔方格模式,基准方格以栔1.34寸为单位。相应地,垂直与水平方向上的两个基本单元尺寸的推算值如下:
垂直方向:材=2.68寸,栔=1.34寸
水平方向:小斗长=4.02寸,斗间=1.34寸
地藏堂斗栱尺寸皆由基准方格a、A(栔、材)所律,且与斗栱实测尺寸相当吻合。进而推析a、A的设计尺寸分别为:a=1.35寸,A=2a=2.7寸,设计尺略小于现行尺。
正福寺地藏堂在尺度设计上,以材、栔为基准,构建斗栱立面构成的材栔方格模式,以及斗栱与朵当的关联构成(图18)。基于材、栔的斗栱与朵当的关联构成为:斗栱全长8.5材,相邻斗栱空当1.5材,合朵当10材、当心间30材。
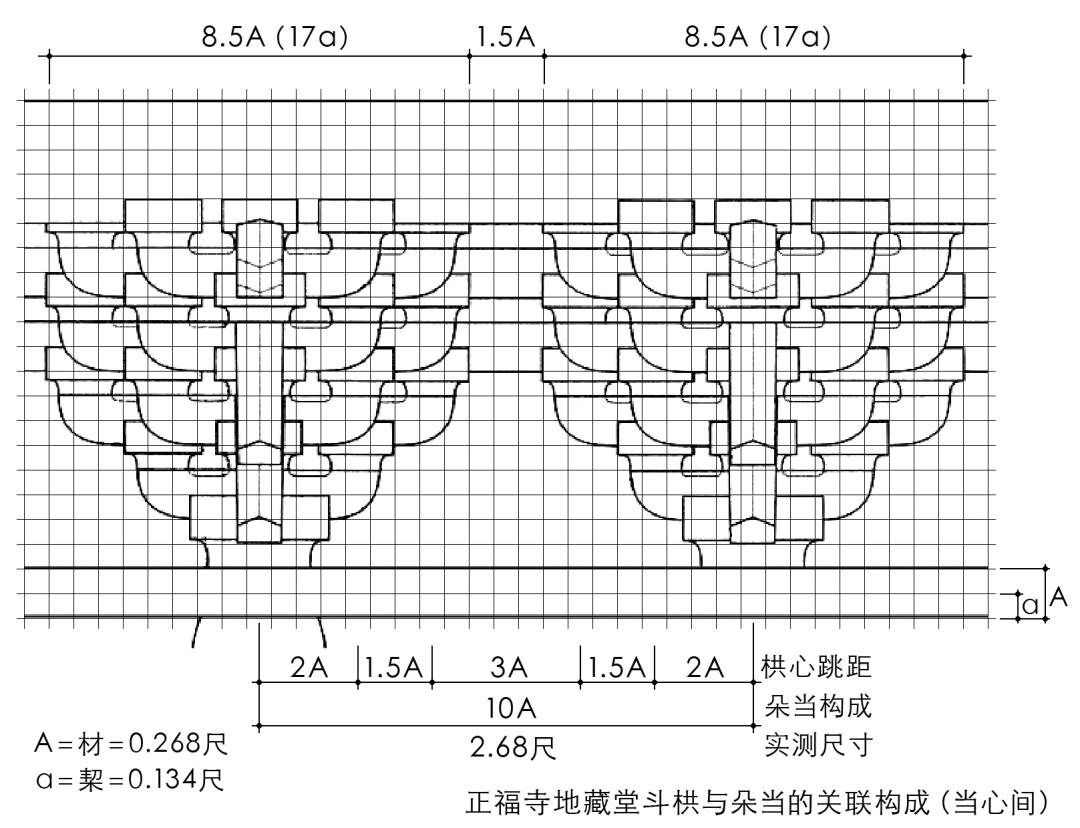
图18 正福寺地藏堂斗栱构成及其与朵当的关联构成
圆觉寺舍利殿是斗栱构成吻合材栔方格模式的另一例,且其斗栱与朵当的关联构成不同于其他关东唐样遗构。
舍利殿上檐斗栱六铺作单杪双下昂,实测材广2.6寸,栔高1.3寸,斗栱立面构成与材栔方格模式相当吻合,其基准方格以栔1.3寸为单位。
舍利殿的特色在于斗栱与朵当的关联构成,其当心间的朵当构成为9.5材,较标准朵当的10材减小0.5材,即斗栱全长8.5材,相邻斗栱空当1材,合朵当9.5材(图19)。相应地,当心间7.4尺,合28.5材;次间5.57尺,合21.5材;副阶4.15尺,合16材(图20)。
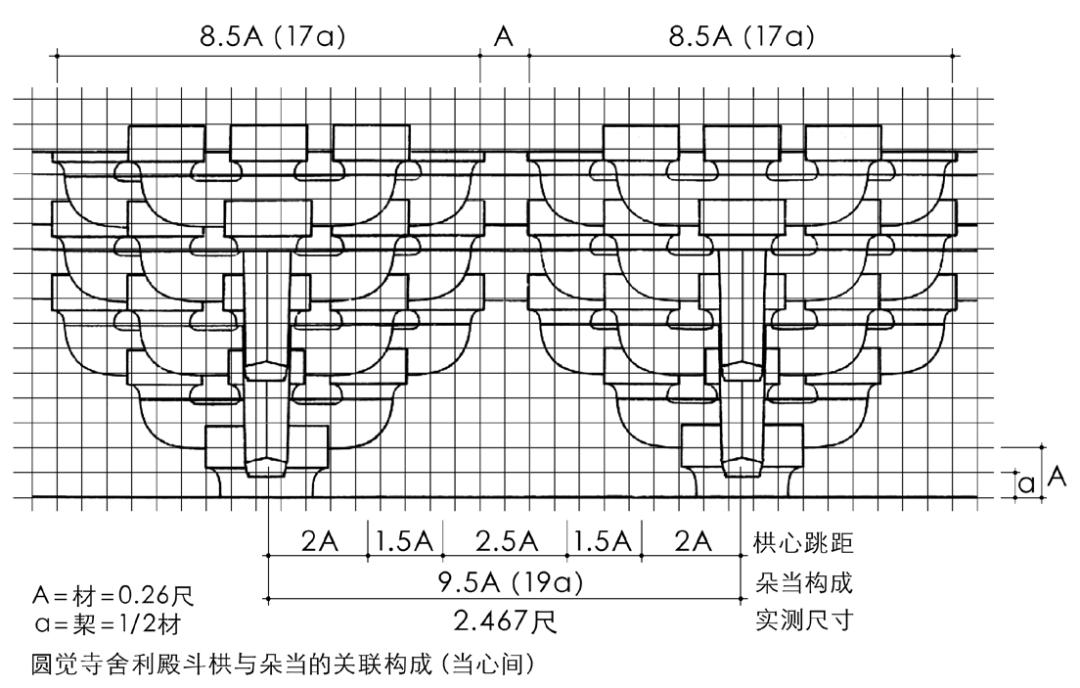
图19 圆觉寺舍利殿斗栱构成及其与朵当的关联构成
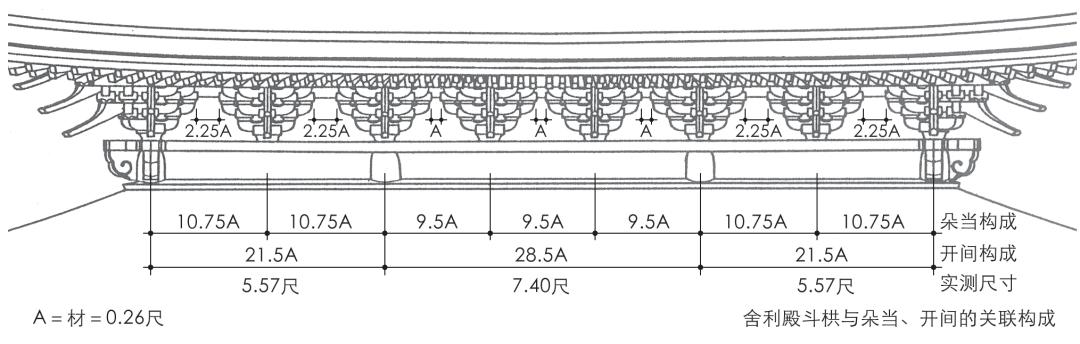
图20 圆觉寺舍利殿斗栱与朵当、开间的关联构成
若以开间、朵当实测尺寸反推材、栔的精确值,则:材=2.594寸,栔=1.297寸。进而推析材、栔的设计尺寸分别为:材=2.6寸,栔=1.3寸,设计尺微小于现行尺。
圆觉寺舍利殿看似不规则的朵当、间广的构成关系中,隐含了材栔模数的权衡和调节。
斗栱立面构成的材栔方格模式,从现存遗构看,以关东唐样佛堂最为典型。关东唐样佛堂的尺度设计特色,表现为以材、栔基准的形式,建立斗栱立面构成关系以及斗栱与朵当的关联构成,而这也正是中世唐样建筑尺度设计的一个基本路径和方法。
唐样斗栱的材栔方格模式,在性质上与《营造法式》用材制度“固定模数单位数,变动模数单位值”的方法一致,即在同一构成模式下,只要变动a、A基准值的大小,即可得到相应的斗栱构件尺寸,这为唐样斗栱的设计与制作带来便利。
唐样尺度设计上,以材、栔为基准,组织和筹划斗栱横向尺度关系及其与朵当的关联构成。材栔格线法是中世唐样斗栱、朵当尺度设计的一种基本方法(图21)。
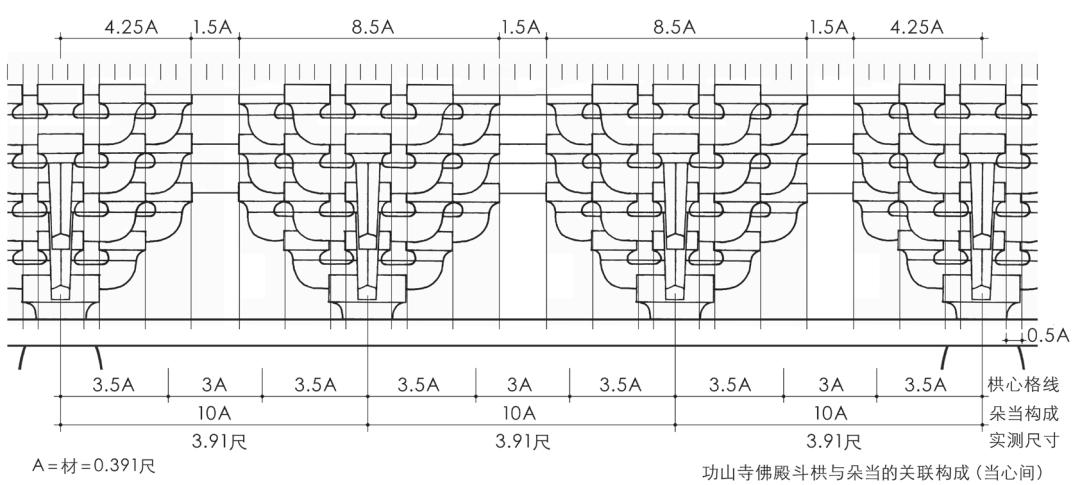
图21 功山寺佛殿斗栱与朵当的关联构成示意
唐样斗栱构成上的材栔方格模式,其进一步的意义在于斗栱与朵当、开间尺度的整体性和关联性的建立。模数基准的“材”贯穿从斗栱到朵当、开间的整体尺度构成,从而完成从斗栱局部到间架整体的尺度模数化演变。
3.3 唐样斗栱构成的斗口方格模式
唐样斗栱构成的斗口方格模式,指以斗口为基准的斗栱立面构成形式。相较于材栔方格模式,斗口方格模式的特点在于:其两向尺度构成由单一的斗口格线权衡,构成关系更为简洁和统一。
中世唐样斗口方格模式成立的基本条件是:
垂直方向:跳高=2斗口
水平方向:小斗长=2斗口,斗间=1斗口
方格两向以斗口为基准,基准方格呈正方形,并以斗口格线的双向控制构成斗栱立面的斗口方格模式(参见前图17)。
基于斗口方格模式,斗栱立面的构成关系如下(设斗口为A):
垂直方向:跳高=2A,大斗高=2A
水平方向:斗间=A,小斗长=2A,大斗长=3A;短栱全长=8A,长栱全长=12A,栱心跳距=3A
上述这一构成模式应是中世唐样斗口模数的基本定式。在斗栱尺度关系上,唐样斗口模数与清式斗口模数基本相同,但唐样较清式更为简洁、明快。
唐样斗栱的斗口方格模式,最终以单一的斗口基准,统一了斗栱两向的尺度关系。模数基准由竖向尺度单位的材栔,转向横向尺度单位的斗口。现存中世唐样遗构中,斗口模数之例有延历寺瑠璃堂、圆融寺本堂、园城寺藏殿、玉凤院开山堂、永保寺观音堂等诸构。
延历寺瑠璃堂为唐样方三间佛堂,斗栱形式为重栱计心造四铺作,实测斗口2寸。综合权衡斗栱及朵当尺寸,推算斗口的精确值为:斗口=2.12寸。瑠璃堂斗栱立面构成吻合斗口方格模式,其基本单元尺寸的推算值如下:
垂直方向:跳高=4.24寸
水平方向:斗口=2.12寸,斗间=2.12寸,小斗长=4.24寸
测值与算值相较,吻合基于斗口的格线关系。此外,大斗尺寸以及栱心跳距,也是斗口模数的一个重要指标,其测值吻合于大斗长3斗口、栱心跳距3斗口的构成关系。
唐样斗口模数的目标,仍在于横向尺度上斗栱与朵当的关联构成,瑠璃堂基于斗口的斗栱与朵当的关联构成如下:斗栱全长12斗口,相邻斗栱空当1斗口,朵当合13斗口。相应地,明间39斗口,次间26斗口,整体91斗口×91斗口(图22)。
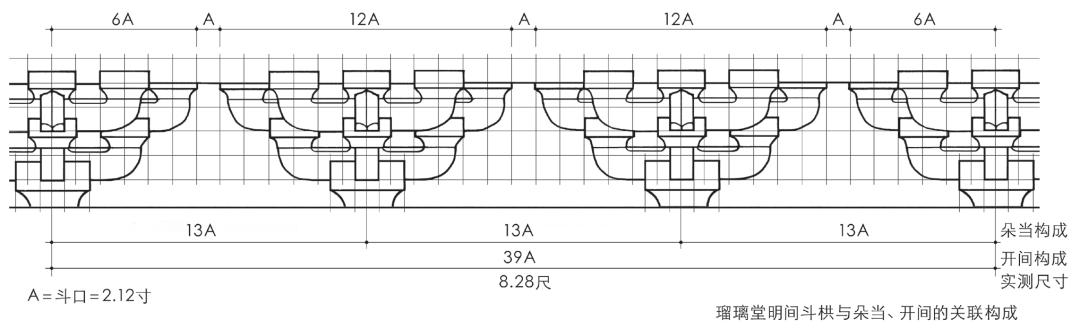
图22 延历寺瑠璃堂斗栱与朵当的关联构成示意
京都玉凤院开山堂基于斗口的斗栱构成,是中世唐样斗口方格模式的又一典范之例。开山堂斗栱形式为重栱计心造四铺作,实测斗口2.9寸。斗栱实测数据分析表明,开山堂以斗口2.9寸为基准,建立斗栱立面构成的斗口方格模式(图23)。开山堂斗栱尺寸皆由斗口所律,且与斗口方格模式十分吻合,其基本单元尺寸的推算值如下:
垂直方向:跳高=5.8寸
水平方向:斗口=2.9寸,斗间=2.9寸,小斗长=5.8寸
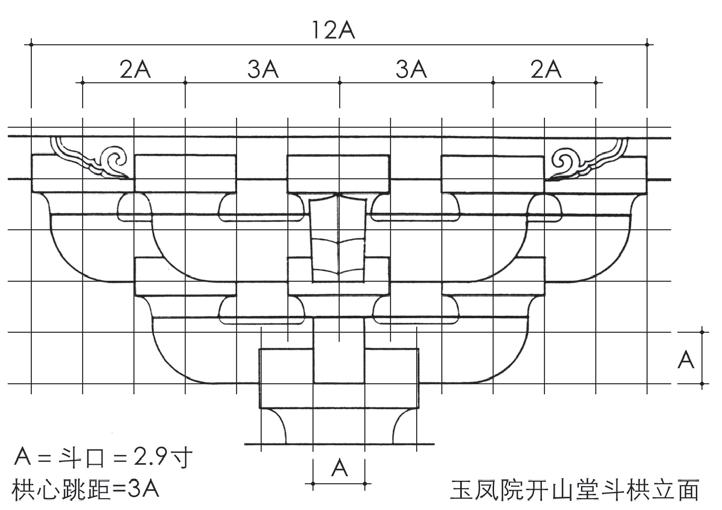
图23 玉凤院开山堂斗栱立面构成的斗口方格模式
上述算值与测值相较,唯跳高的测值微大于算值,其他则十分吻合。
开山堂斗栱正侧两向之栱心跳距同为8.7寸,皆以3斗口为则。唐样斗口模数的栱心跳距,由宋式的2材转为清式的3斗口形式(图24)。
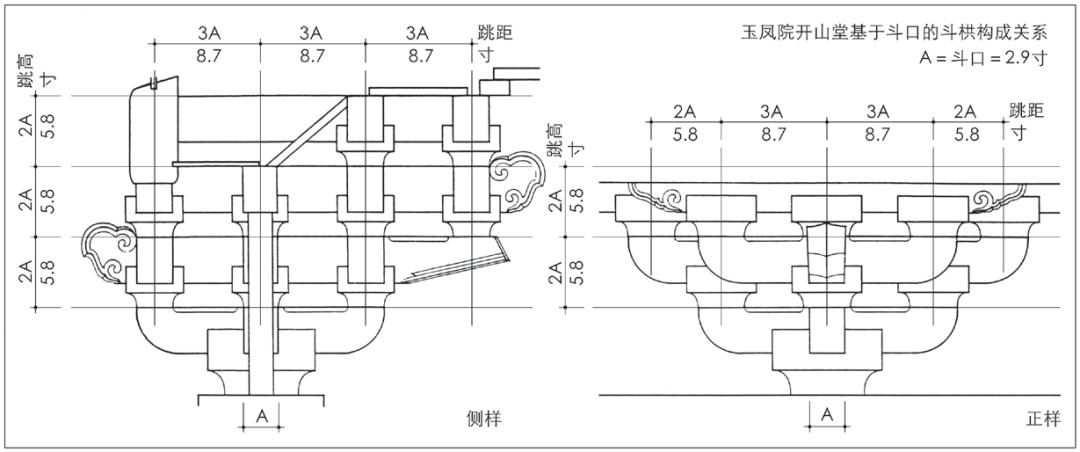
图24 玉凤院开山堂基于斗口的栱心跳距构成关系
关于唐样斗口模数,永保寺观音堂是不可忽视的一例,其中有着值得讨论的问题和线索。
岐阜县永保寺观音堂为方三间带副阶的形式。关于其建立年代,日本学界认为在14世纪初(1314年),然根据观音堂斗栱构成关系的分析,这一断代或有疑问和值得探讨之处。
观音堂的一个重要特色是其基于斗口的斗栱构成关系。观音堂各间无补间铺作之设,斗栱形式为唐样重栱造四铺作,实测斗口2.3寸。综合权衡斗栱尺寸及其构成关系,可推得斗口的精确值为2.25寸,与斗间尺寸相同,其斗栱立面构成吻合于斗口方格模式(图25)。
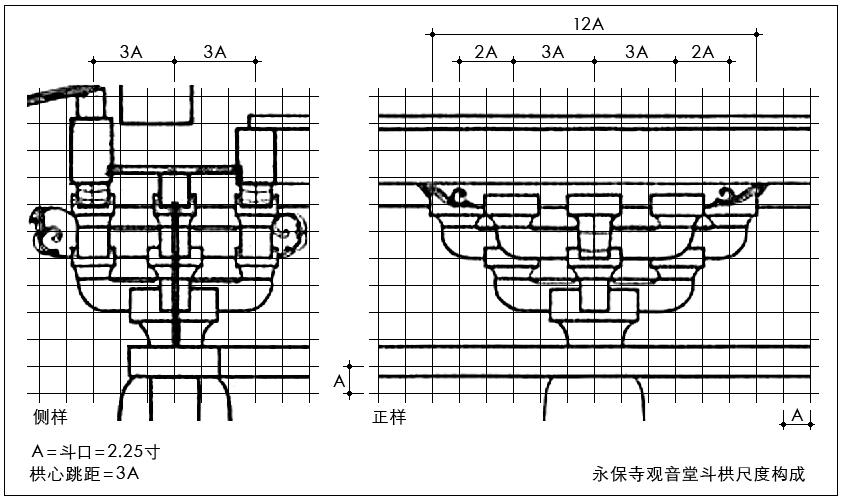
图25 永保寺观音堂基于斗口的斗栱立面构成
观音堂斗口方格模式的基本单元尺寸的推算值如下:
垂直方向:跳高=4.5寸
水平方向:斗口=2.25寸,斗间=2.25寸,小斗长=4.5寸
实测栱心跳距6.75寸,合3斗口。观音堂斗栱测值与算值相当吻合,斗栱构成基于以斗口2.25寸为单位的双向格线关系。
永保寺观音堂基于斗口的斗栱构成关系,与玉凤院开山堂、延历寺瑠璃堂完全一致,即:小斗长2斗口,斗间1斗口,跳高2斗口,栱心跳距3斗口,斗栱全长12斗口。
上述这一斗口方格模式,应是室町时代(1336—1573年)后期唐样斗栱构成的一个定式。在斗栱比例关系上,足材与斗口之比转为2倍关系,是明清斗口模数的一个重要标志。与清式斗口模数相较,上述唐样三构斗栱构成上的几个标志性斗口关系,都与清式规定相同或相仿。
以日本学界所推定的观音堂建立年代(1314年)观之,观音堂在现存唐样遗构中为年代最早者,然而问题在于:这一断代与斗口模数的时序性不符,且相差甚大。如果观音堂斗口模数的分析成立的话,那么其建立年代应推后至16世纪前后。观音堂斗栱构成的分析,为其年代判定提供了一个参考依据。
就中国本土的技术逻辑而言,斗口模数应是材栔模数的演变形式,然对于日本建筑而言,并非简单的线性演变关系。唐样设计技术的演变历程,应非单线式和连续性的,而是多源头和分段式的。
3.4 六间割的斗长模数形式
作为尺度基准的一个形式,斗长在唐样斗栱构成上,具有独特的意义。
对于注重横向尺度关系的唐样尺度设计而言,斗长基准是最为直接和直观的基准形式,室町末以来斗长模数逐渐成为主流的变化说明了这一点,而最终定型的六间割斗长模数,正是这一变化的表现和结果。
唐样斗长模数自中世初期以来,经历了东大寺钟楼连斗式的原始斗长模式(图26),至16世纪的圆觉寺佛殿古图,已是成熟的斗长模数形式。二者斗栱构成上的斗长模数,在本质上同样都是基于栱心格线的变化与改造,基本上仍是宋式风范的延续。而中世后期出现的六间割斗长模数,则具有显著的日本化特征。近世(1573—1868年)以后,六间割斗长模数逐渐定型和制度化,并作为唐样设计技术规制,收录于唐样建筑技术书。
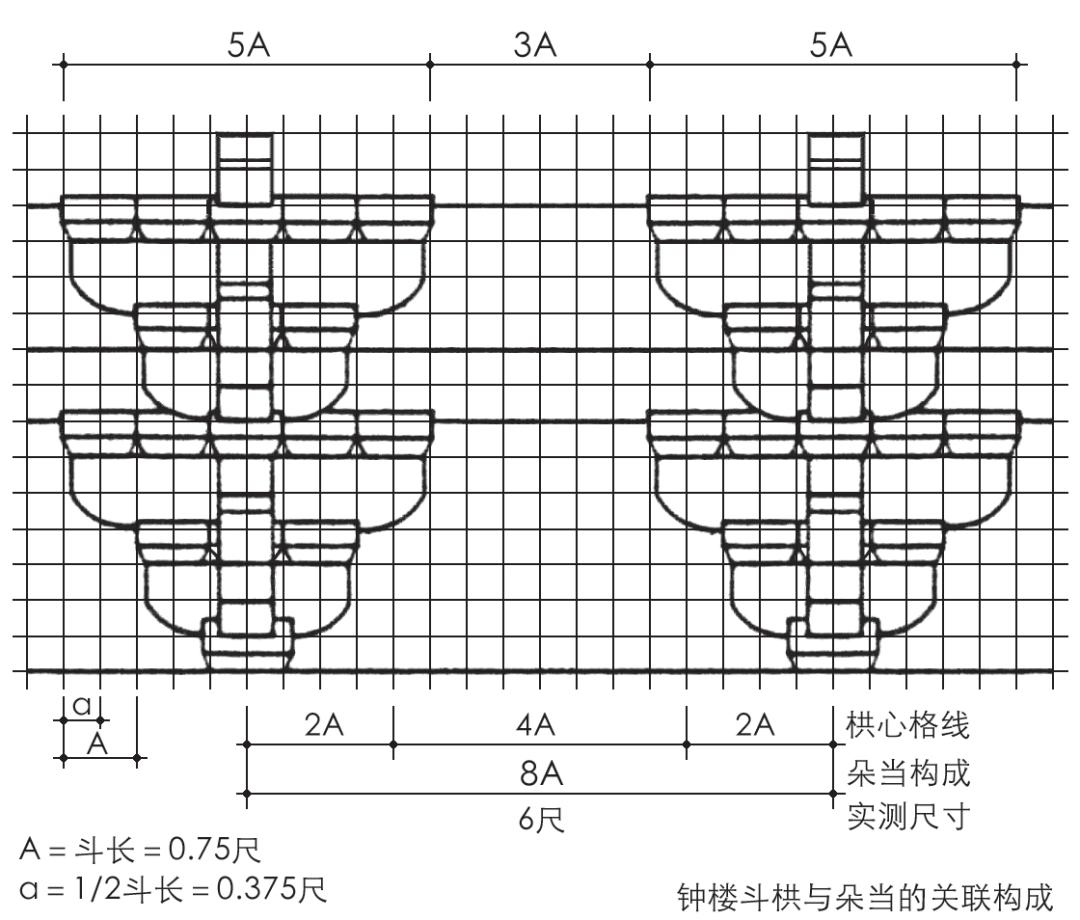
图26 东大寺钟楼斗栱与朵当的关联构成
所谓“六间割”斗长模数,为近世唐样建筑技术书中的术语,指室町时代后期出现的六斗长朵当的构成形式以及相应的斗栱、开间尺度设计方法,即以朵当的1/6为小斗长,并以此斗长为基准,权衡和设定斗栱、朵当及开间的尺度关系。
六间割斗长模数的意义在于:以文献制度的形式,明确了斗栱构成与朵当、开间构成的的关联性和整体性。六间割斗长模数注重的是横向尺度的构成关系。
现存中世唐样遗构中,六间割斗长模数见于永保寺开山堂与酬恩庵本堂二例。
永保寺开山堂为唐样方三间佛堂,当心间补间铺作两朵,间广7.74尺,朵当2.58尺;斗栱为唐样六铺作单杪双下昂的形式,实测小斗长4.3寸,斗间1.3寸。
基于斗栱、朵当及开间的关联构成分析,当心间朵当构成合6斗长、18斗间,依此推算斗长、斗间的精确值为:小斗长=4.3寸,斗间=1.433寸。以此斗长、斗间之值,权衡开山堂斗栱实测尺寸,开山堂斗栱立面构成吻合斗长格线模式,基准格线以1/3斗长的斗间1.433寸为单位。
开山堂斗栱立面构成上,其斗间与斗长的比例关系,由此前的1/2变化为1/3。在斗栱与朵当的关联构成上,斗栱全长(5+2/3)斗长,相邻斗栱空当1/3斗长,合朵当6斗长。其当心间朵当2.58尺,与小斗长0.43尺呈六倍关系,开山堂斗栱、朵当及开间的尺度构成,统一于斗长基准。这一构成关系正是所谓“六间割”的斗长模数形式。
中世唐样遗构中六间割斗长模数的另一实例是室町时代后期的京都酬恩庵本堂。
酬恩庵本堂平面为方三间形式,当心间补间铺作两朵,次间补间铺作一朵,实测当心间9尺,次间6尺,朵当逐间等距,各3尺。
本堂斗栱为唐样五铺作单杪单昂形式,实测小斗长5寸,斗间1.6寸。权衡小斗长5寸与朵当3尺的关系,二者间呈六倍关系,即:小斗长=1/6朵当,且斗间=1/3小斗长。基于斗栱、朵当及开间的关联构成分析,本堂朵当构成合6斗长、18斗间,依此推算斗长、斗间的精确值为:
小斗长=5寸,斗间=1.67寸
以此斗长、斗间之值,权衡本堂斗栱实测尺寸,横向尺度上吻合斗长格线关系,且以1/3斗长的斗间为细分基准;进而,在斗栱与朵当的关联构成上,以斗长为基准,构成关系一如永保寺开山堂的斗长模数形式。
六间割斗长模数成立的基本条件如下:小斗长等于1/6朵当,斗间等于1/3小斗长。进而,斗栱与朵当的关联构成为:斗栱全长(5+2/3)斗长,相邻斗栱空当1/3斗长,合朵当6斗长。相应地,在间广构成上,以朵当、斗长为两级模数形式:当心间3朵当、18斗长;次间2朵当、12斗长(图27)。
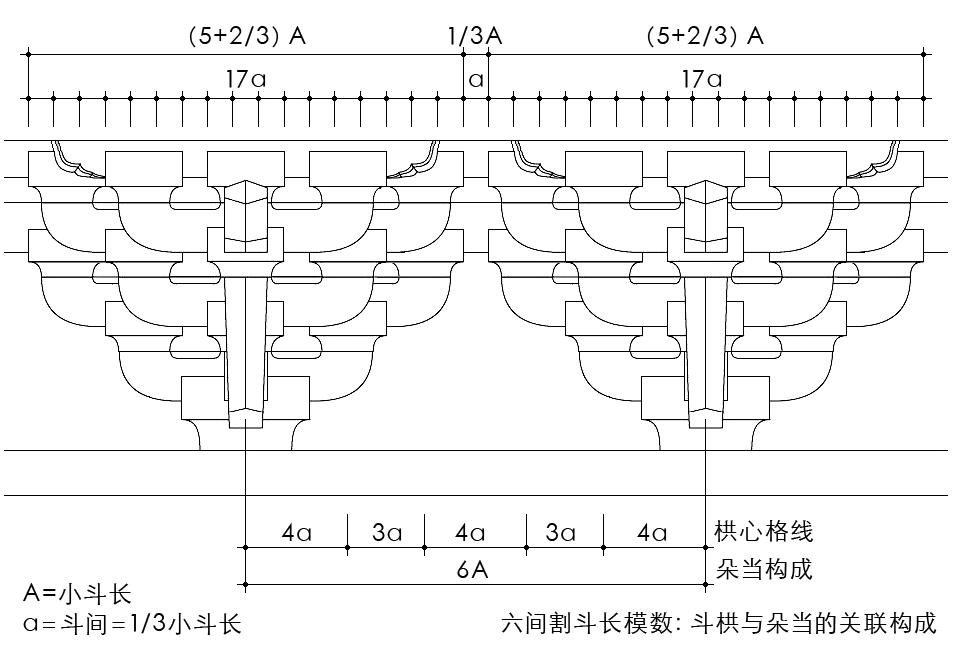
图27 六间割斗长模数:斗栱与朵当的关联构成
六间割斗长模数,以斗长的1/3为细分基准,在斗栱构成以及斗栱与朵当的关联构成上作精细筹划。室町时代后期,由于对横向尺度关系愈加注重,唐样尺度构成上材栔的基准属性,基本上已转移至更为直接和直观的斗长基准上。
实际上,中世唐样佛堂的尺度设计,无论材栔模数、斗口模数和斗长模数,在横向尺度构成上,最终都可转换成斗长基准的形式,并通过斗间与斗长比例关系的设定,组织和筹划斗栱构成以及斗栱与朵当的关联构成。或者说,在斗栱与朵当的关联构成上,建立“朵当-斗长-斗间”三者间的简洁比例关系。
3.5 唐样斗栱构成的二材关系
《营造法式》斗栱制度的分析表明:栱心跳距的二材关系是宋式斗栱构成的基本比例关系,而传承宋式的唐样斗栱,同样遵守二材关系这一宋式规制。根据唐样斗栱材栔方格模式的计算,其栱心跳距为4栔、2材。也就是说,唐样斗栱材栔方格模式中,传承和隐含了宋式斗栱构成的二材关系,二材关系仍是唐样斗栱构成的一个基本定式。
唐样斗栱构成上的二材关系,是认识唐样斗栱与宋式关联性的一个重要线索。现存唐样遗构中,栱心跳距吻合二材关系是一个显著特征。若论尺度关系上唐样斗栱与宋式的关联性,其典型地表现在如下两点:一是基于栱心格线的尺度筹划,二是栱心跳距的二材关系。
材栔模数向斗口模数的转换,是设计技术由宋式向清式演变的表现和标志。在栱心跳距的设定上,宋式为2材,清式为3斗口,二者本质相同,即以材厚10份计,二者皆为30份。基于这一转换关系,宋式斗栱构成的二材关系,相应地转化为清式斗栱构成的三斗口关系,二者性质上是同一尺度关系的不同阶段形态。
中世唐样斗栱构成上,同样重复了由宋至清的演变轨迹,斗栱构成的基准,由材栔转向斗口,材栔方格模式转为斗口方格模式。相应地,栱心跳距的二材关系亦随之转化为三斗口关系。然唐样斗栱材广厚比例为5∶4或6∶5,不存在宋式的转换机制,故唐样斗栱构成上二材关系向三斗口关系的转换,并非自身演变的结果,而是与明清技术的联动和呼应。
唐样斗栱构成上二材关系向三斗口关系的转换,表明继宋技术之后,明清技术对唐样建筑影响的存在。
4 整体尺度模数化的一环:斗栱与朵当的关联构成
4.1 斗栱与朵当的关联构成
尺度规律研究上,孤立的斗栱分析是没有意义的,唯有将其置于整体关系中,或者说置于斗栱与朵当的关联构成中,方显示出其意义所在。基于此,成熟的斗栱尺度设计应包括两个方面的内容:一是斗栱自身尺度的比例化和模数化,二是斗栱与朵当的关联构成,且斗栱构成和斗栱与朵当的关联构成,是一个整体的两个层次,二者在尺度关系上互为依存。也就是说,唐样斗栱尺度构成的实证,在于斗栱与朵当的关联构成的认识。
尺度设计技术的分析表明:大尺度的间架与小尺度的斗栱之间的尺度关联,是以朵当为中间环节而勾通、递进和实现的;而朵当构成的模数化,又是通过斗栱与朵当的关联构成完成的。
斗栱与朵当的关联构成的建立,意味着以模数的方式,精细组织和筹划斗栱与朵当的尺度关系。从宋式到清式莫不如此,唐样建筑亦采用的是这一思路和方法。因此,栱心格线的意义,不只在于斗栱自身比例关系的权衡设定,随着补间铺作以及重栱造的出现,栱心跳距对朵当及间广的影响也愈趋显著,尤其表现在扶壁栱横向尺度的组织与筹划上。
从现存遗构来看,江南五代宋初,补间铺作两朵以及扶壁重栱做法已相当普及和成熟,这使得扶壁栱排布密集,空当狭小,其横向尺度的精细筹划已显得迫切和必要。而北方唐宋建筑中,虽补间铺作尚未成熟,然通过隐刻扶壁栱的形式,补间扶壁栱形象也相当丰富和充实,横向尺度上小斗排布匀整而规律。根据分析,这一时期扶壁栱横向尺度的组织与筹划,应有相应的设计方法,而以栱心格线的方式,组织和筹划扶壁栱的横向尺度关系则是一个显著特色。其最直接和直观的方法是:以开间尺寸的比例细分,权衡、设定栱心格线关系,且以均分开间的方式较为多见和典型,如高平游仙寺毗卢殿的扶壁栱尺度设计中,逐层交隐的栱、斗匀整排布,栱心格线的尺寸为间广的1/8(图28)。
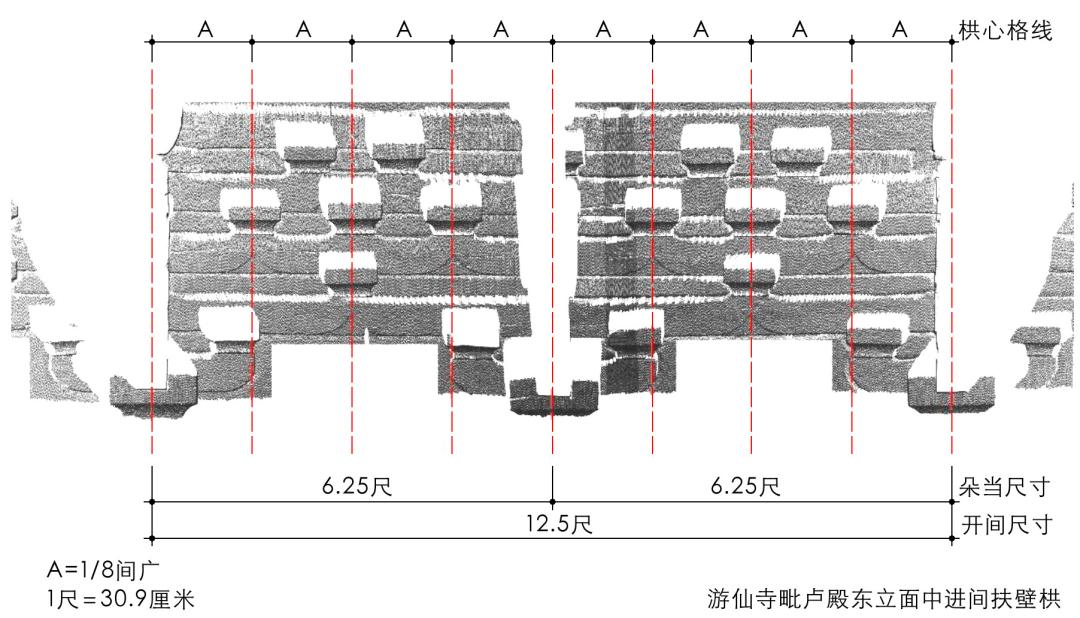
图28 游仙寺毗卢殿扶壁栱及栱心格线设计
这一时期的斗栱尺度设计,在横向尺度的组织与筹划上已颇具匠心,扶壁栱设计及其横向尺度的筹划,已与朵当、间广产生互动关联,初具斗栱与朵当、开间的尺度关联性意识,如以栱心格线的方式,权衡斗栱的横向尺度关系,进而建立斗栱与朵当、开间的关联构成。
随着栱心格线性质和功能的演进,栱心格线有可能逐渐从与间广的互动关系转变为支配因素,最终栱心跳距成为权衡、筹划横向尺度关系的一个基准单元。而这一特点在日本中世唐样建筑尺度设计上,表现得尤为显著和典型,主要表现在如下两个方面:
一是唐宋栱心格线法的细化与拓展;
二是栱心格线性质的进化,即在斗栱与朵当、开间的关联构成上,由之前的互动关系转为支配关系。
以唐样神角寺本堂(1369年)的栱心格线法再作比较。
本堂尺度构成的特色,表现在基于栱心格线的横向尺度关系上。本堂开间设计尺寸为:当心间8尺,次间7尺,栱心跳距0.8尺。本堂尺度设计上,栱心跳距为朵当的1/5、当心间的1/10;相应地,斗间为1/3栱心跳距,小斗长为2/3栱心跳距(图29)。
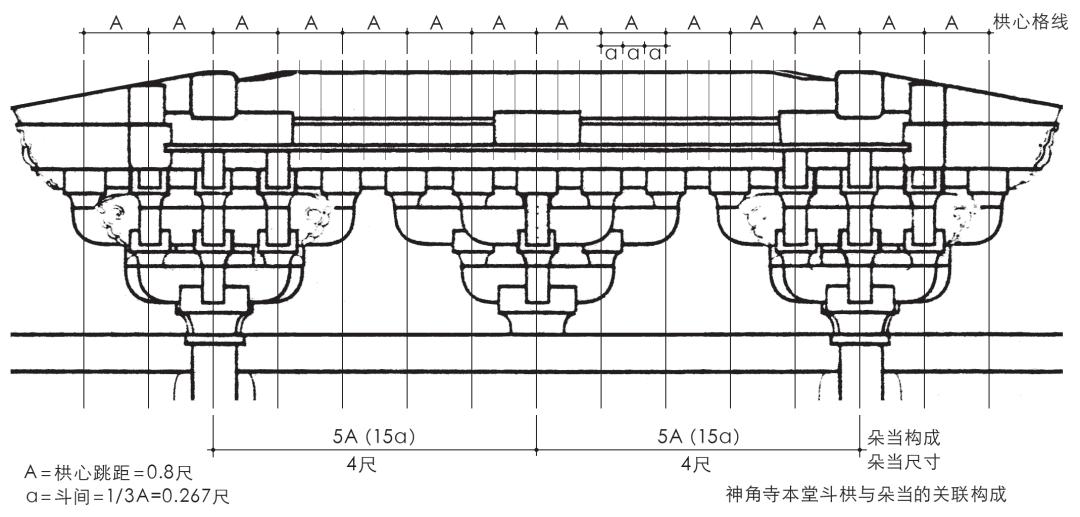
图29 神角寺本堂斗栱与朵当的关联构成
4.2 尺度关系的层次与序列
斗栱构成的格线形式,就斗栱本身而言,其意义在于斗栱尺度关系的组织和筹划;而就整体尺度关系而言,其意义在于成为从斗栱到间架的整体尺度模数化序列上的一环。
唐样斗栱与朵当的关联构成,是以基于栱心格线的小斗配置作为横向尺度组织与筹划的基本方法的。实际上,基于栱心格线的斗栱、朵当的横向尺度关系,可简化和抽象为小斗长、斗间及相邻斗栱空当这三个要素的组合和变化。进而根据斗间、相邻斗栱空当与小斗长的比例关系,上述三个要素的组合和变化,可进一步简化和抽象至“斗间”这一个要素上。
对于斗栱构成而言,前述唐样斗栱构成模式虽各有不同,然三者的共同特点是皆以“斗间”为细分基准,且斗间与小斗长建立简洁的比例关系,即斗间为小斗长的1/2、1/3或1/4,从而以斗间这一细分基准,精细筹划斗栱的横向尺度关系。
对于朵当构成而言,在斗栱构成模数化的前提下,相邻斗栱空当的组织和筹划,也就成为朵当构成模数化的关键所在。故其方法是将相邻斗栱空当纳入斗栱构成关系中一并筹划,从而使得朵当构成与斗栱构成相关联和一体化。
斗栱与朵当的关联构成的实质是:相邻斗栱空当与小斗长的比例关系的建立。正是这一微小细节,显示了唐样斗栱在横向尺度组织和筹划上的匠心所在。
在横向尺度关系上,以小斗长的分数,精细筹划斗栱构成以及斗栱与朵当的关联构成,是唐样模数设计的特色所在。唐样基于各种基准的模数设计方法,其基本思路都是通过权衡斗间和小斗长的比例关系而实现的。
唐样尺度设计上,微观细节反映全局和整体的设计意匠,在有意识地精细筹划斗栱与朵当的关联构成上,唐样或甚于宋清法式。
以朵当为核心的唐样模数构成,包括如下两个关系:一是层级关系,一是序列关系。以六间割斗长模数为例,其模数构成的层级关系为:以朵当为基本模数,以斗长、斗间为次级和细分模数;其模数构成的序列关系为:以朵当的倍数和分数,权衡和设定开间及斗栱的尺度关系;其横向尺度的组织和筹划,基于如下分层递进的格线关系:开间构成的朵当格线、朵当构成的斗长格线、斗栱构成的斗间格线(图30)。
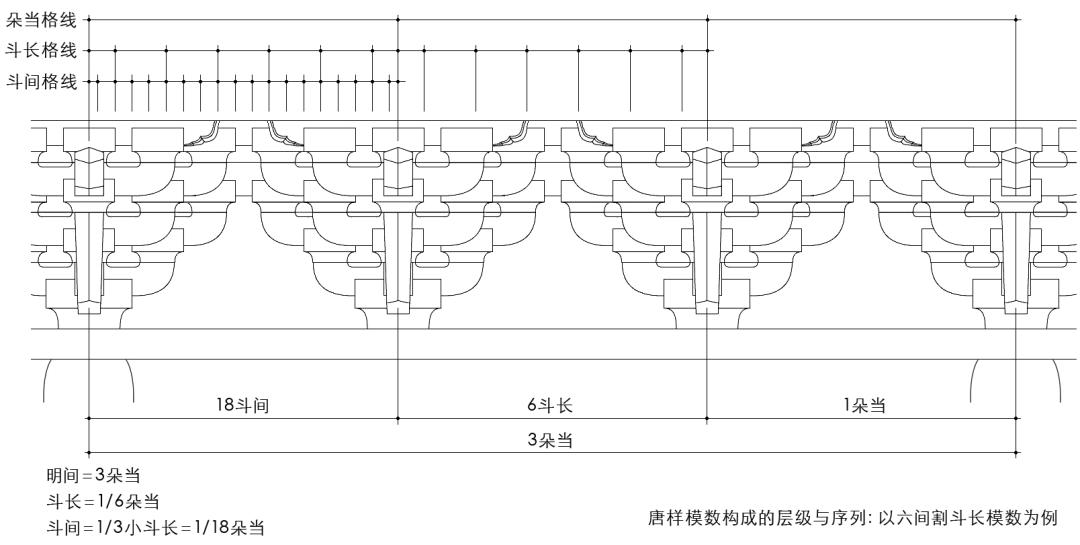
图30 唐样模数构成的层级与序列
斗栱尺度的组织筹划以及朵当、开间尺度的权衡设定,在成熟的模数体系中是一个相互衔接和关联互动的整体。古代建筑尺度设计技术的演变过程,是一个间架大尺度与构件小尺度之间逐步关联一体化的过程,而斗栱与朵当的关联构成的建立,则是这一进程中的关键环节。
要之,唐样设计技术演变的关键,主要体现在如下两个关联环节:整体尺度模数化的关键,在于斗栱与朵当的关联构成的建立;而斗栱与朵当关联构成的关键,又在于相邻斗栱空当与小斗长的比例关系的建立。唐样设计技术的演进,大致是沿着这条主线而展开、变化和完成的,而这也正是唐样设计技术的逻辑所在。
尺度比例设计上的格线法,是中国古代设计理念与方法的一个重要特点,反映了设计技术中寓繁于简的思维方式,其实质是以单一基准权衡和把握整体尺度及比例关系。格线法在中日古代建筑设计上皆有丰富和典型的表现,基于格线法的模数思维,中日是同源和共通的。
微信编辑:张维欣
责任编辑:杨 澍
审核:赵 荣
作者简介
张十庆,东南大学建筑研究所教授,博士,主要从事古代建筑技术史研究。
公众号图文有删节,完整阅读请参见。版权所有,转载请注明出处。本文标准引文格式如下,欢迎参考引用:
张十庆. 基于栱心格线的斗栱构成:中日斗栱尺度设计的比较分析[J]//建筑史学刊,2023,4(1):4-17.
原标题:《学术丨张十庆:基于栱心格线的斗栱构成:中日斗栱尺度设计的比较分析》
本文为澎湃号作者或机构在澎湃新闻上传并发布,仅代表该作者或机构观点,不代表澎湃新闻的观点或立场,澎湃新闻仅提供信息发布平台。申请澎湃号请用电脑访问http://renzheng.thepaper.cn。





- 报料热线: 021-962866
- 报料邮箱: news@thepaper.cn
互联网新闻信息服务许可证:31120170006
增值电信业务经营许可证:沪B2-2017116
© 2014-2025 上海东方报业有限公司




