如果没有被罗马士兵杀死，阿基米德能发明微积分吗？

公元前214年，古罗马名将马塞勒斯率领大军袭击古希腊的叙拉古，却被阿基米德的弹弓和机械爪挡在城下。罗马军队的统帅不禁感叹：“这是一场罗马军队和阿基米德一个人的战争！”

但是，今天，阿基米德最伟大的遗产不在于弹弓和阿基米德之爪，而在于几何学。他清晰的论点、他对无穷的把握，以及他已经非常接近微积分的成就。或许，如果再给他一点点外力的推动，他是不是就能到达微积分领域了？那样的话，微积分在地球上出现的时间会比现在早几千年吗？

谈到阿基米德，最为人所熟知的，是他那句：“给我一个支点，我就能撬动地球。”阿基米德享有“力学之父”的美称，与高斯、牛顿并列为世界三大数学家，数学界的“诺贝尔奖”菲尔兹奖奖章上的那个头像就是他。

但当微积分的萌芽在阿基米德的头脑中慢慢成形的时候，一名罗马士兵杀死了他。如果没有被罗马士兵杀死，阿基米德会不会发明微积分？让我们跟随一本微积分启蒙书《欢乐数学之疯狂微积分》，来到两千年前，看看当时到底发生了什么。

《欢乐数学之疯狂微积分》，作者是获得文津奖推荐的《欢乐数学》作者、耶鲁天才老师本·奥尔林。

奥尔林总结了自己10余年的教学精华，用28个故事和400幅火柴人漫画，讲透了微积分原理精髓。其中包含微积分这种思想的历史由来、基本概念、微积分原理的形象解释、充满趣味、锻炼思维的谜题，以及微积分在生活中的应用。

中科院院士、数学家、“微积分爷爷” 林群 高度赞赏：

“这本《欢乐数学之疯狂微积分》既给大家剖析了微积分的底层思维，又充满了非常有趣的案例。它对学习者和教学者都有很大的启发意义，我非常高兴把这本书介绍给大家。”

固定布局

工具条上设置固定宽高

背景可以设置被包含

可以完美对齐背景图和文字

以及制作自己的模板

以下摘文选自《欢乐数学之疯狂微积分》第24章“与众神作战——在这一章，微积分击退了罗马人的进攻”

你知道罗马人是怎样的吧？他们骁勇善战、不苟言笑，建造的大理石“垃圾”在世间遗留千年。在公元前212年，他们的军队来到西西里海岸，想要征服顽强抵抗的小城锡拉库萨。正如历史学家波利比乌斯（Polybius） 所描述的那样，罗马人全副武装而来，乘坐的60艘大船上“载满了弓箭手、 投石手和标枪手”，更不用说船上那4架巨型攻城云梯了。

但是，锡拉库萨人也知道那句古老的谚语，即“如果你在罗马人的地盘上，罗马人怎么做，你就怎么做”。也就是说，他们现在要做的就是和罗马人一样殊死搏斗。因此，锡拉库萨人用大大小小的弹弓发射出巨大的石块、铅块和大量的铁飞镖。然后庞大的机械爪子从城墙内伸出，钳住罗马 的战舰并狠狠摔下，这些船只“撞上陡峭的岩石”，“沉入了海底”。

历史学家普鲁塔克（Plutarch）这样写道：“罗马人眼睁睁地看着军队被一种不可见的方式击溃，开始怀疑自己是不是在与众神作战。”

事实上，情况比他们想象的更糟：对手不是众神，而是阿基米德。

如果要你说出一个有史以来最伟大的数学家，阿基米德是个相当可靠的第一选择。伽利略称他为“超人”。莱布尼茨对阿基米德赞赏有加，说他拔高了人们对天才的期待，在他的光环之下，后来的思想家们都显得平平无奇。

伏尔泰则写道：“阿基米德比荷马更富有想象力。”诚然，阿基米德从未获得过数学界最著名的菲尔兹奖，但有一件事却能证明他的地位之高：菲尔兹奖章正面上的那个头像就是他本人。

你想感受一下他有多聪明吗？去拿一个正方体过来，然后把它小心地切成三部分。

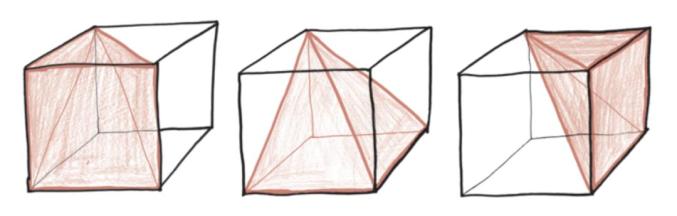
这三部分就像三个形状、大小完全相同的金字塔，而每个金字塔都有一个正方形的底部和一个尖顶。因此，每个金字塔的体积都必须恰好是原来立方体的1/3。

到目前为止，一切都很顺利，不过我们才刚刚开始。拿起其中一个金字塔，把它横向切成无数片，每一片都要非常薄。如果我完成得不错——毕竟我的刀工笨拙，你最好还是用一把无穷概念刀来检查我的工作成果——每个横截面都应该是一个完美的正方形。

最底部的正方形正好就是原来立方体的底部，而最上面的那个正方形则很小很小，只是一个点。在这两个极端之间是无数个中等大小的正方形。

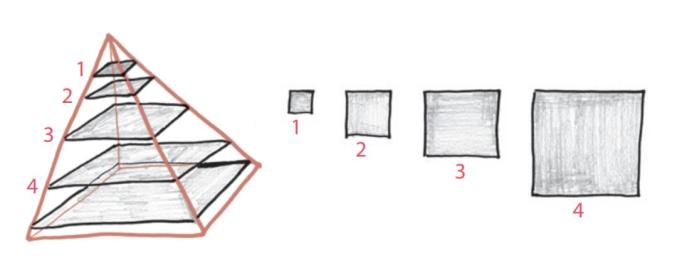
现在，让我们更进一步。把这些方块想象成无限张纸牌，每一张都很薄。如果将它们重新排列，叠放起来的整体体积并不会改变。这一次，在叠放的时候，我们让每个正方形的其中一个角重合。你可能会问，为什么不能把它们扶正，让每个正方形的几何中心重合呢？当然能了，这样一来，就把我们时髦的不对称金字塔改造成了经典的埃及金字塔风格。

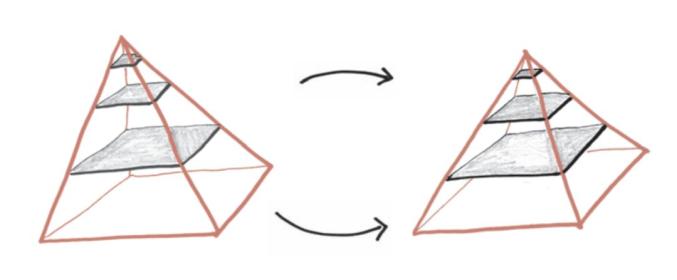
正如此前所说，整体的体积不会改变，仍然是最初那个立方体体积的1/3。

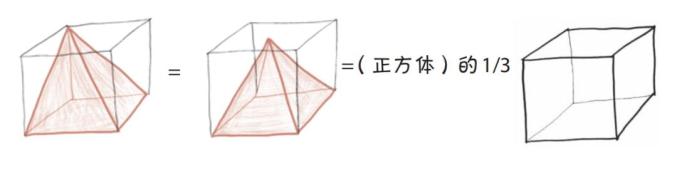
现在，我们得到了计算立方锥体积既巧妙又简便的方法。在1800年后， 当数学家博纳文图拉·卡瓦列里（Bonaventura Cavalieri）重新发现这个方法时，他用自己的名字将其命名为“卡瓦列里原理”。

事实上，这个方法最初起源于公元前5世纪的安提丰(Antiphon，公元前426—前373年，在哲学和数学领域都有突出贡献。在解决“化圆为方”的问题上，提出了“穷竭法”。)，与公元前4世纪欧多克斯（他首先提出了我现在介绍的论证过程）的方法一起发展，在公元前3世纪阿基米德（我们很快会讲到他的突出贡献）的时代达到了无与伦比的高度。为了纪念罗马人 的恐慌，我将把它命名为“无穷灾难原则”。

这个方法很简单。在一个三维图形中，当你将横截面的形状从正方形换成其他面积相同的形状时，它的体积并不会受影响。例如，我们可以把正方形换成等面积的长方形，现在这个被拉长的金字塔的体积仍然占了之前立方体的1/3。

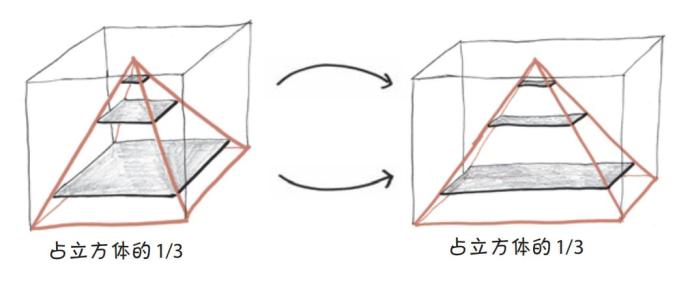
或者在大师级别的终极游戏中，我们还可以把这些方形都变成圆形。严谨地说，用纸笔这样画图只能“化圆为方”，而且在实践中，这是不可能 做到的。“事必躬亲”是为体操运动员准备的名词，而我们只能在纯几何的天空中滑翔。想象一下，每个正方形都慢慢地变成一个圆，同时它们的面积永远不变。

我们的金字塔变成了圆锥体，立方体变成了圆柱体。因此，一个圆锥体的体积刚好是和它等底等高的圆柱体体积的1/3。

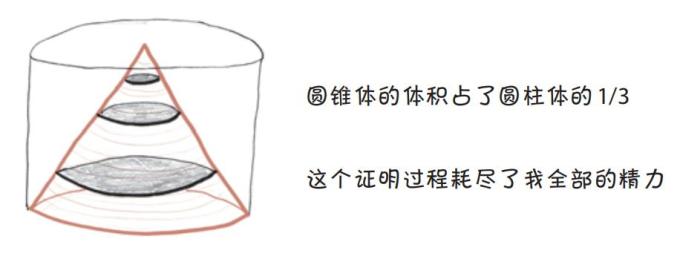
很酷，对吧？公元2世纪，普鲁塔克滔滔不绝地说：“在几何学中，不可能找到比这更困难、更复杂的问题，也不可能 找到比这更简洁明了的证明……你进行再多的研究也无法获得证据，然而，一旦看到这样的证据，你会立刻相信自己已经发现了它。阿基米德通过如此顺利和快速的路径引导你得到所需的结论。”

不过，这些几何级别的思考并不能让阿基米德得到“军事天才”的美誉。人们不禁要问：阿基米德那台摧毁罗马军队的战争机器从何而来？

普鲁塔克坚称：“他设计和制造这些机器时，并没有把它们当成什么重要的事，只是作为几何学上的消遣活动。”虽然这听起来很奇怪，但这就是数学史中的基本模式。漫无目的地航行在幻想之旅中，然后以某种方式在 未来带来技术上的突破。

虽然罗马人不太喜欢纯粹的数学探究，但他们肯定敬畏能一举摧毁船只的“死亡之爪”。马塞勒斯将军在意识到自己犹如反派后（就像《小鬼当 家》中的反派一样），便和他的部队撤退了。

几个月后的一个下午，阿基米德正在沙地上绘制图表。我更愿意认为他当时正在重温他最喜欢的那个证明过程，也就是他让朋友和家人在他的墓碑上刻的那个定理。那个始于一个球体的定理。

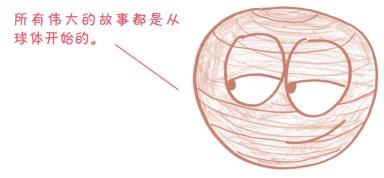
我们把这个球装到一个圆柱体里，使它与圆柱体完美贴合，就像自动发球机里的网球一样。

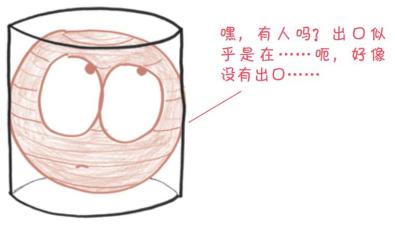
阿基米德的问题是，球的体积占了圆柱体的多少？（事实上，他的问题更直接一些：球的体积有多大？但是任何对于物体 大小的描述都需要有参照物。例如，把单位英尺作为参照物，我的身高大约为五又三分之二英尺——这就是此处圆柱体的作用所在。）

首先，把整个球对半切开。我们不是把网球放在一个完美贴合的容器里，而是把一个半球放在一个冰球里。

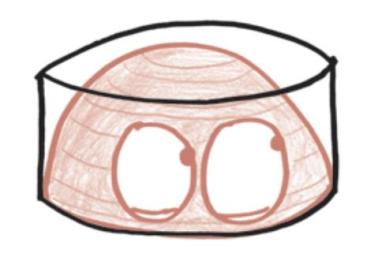
现在，我们不考虑半球的内部容积，先来看看它外部的体积。本着“无穷灾难原则”，我们可以把这部分想象成一堆叠起来的圆环，而且每个圆环的中间都切一个圆洞。

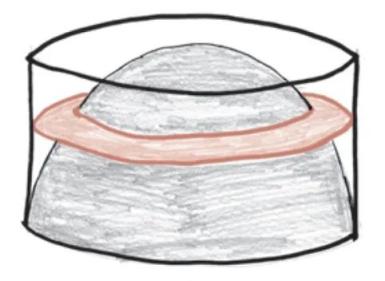
这一堆圆环的最底部是一个超细的环，它中间的洞非常大，几乎占据了整个圆环，只留下一圈极细的边。与此同时，顶部是一个非常粗的圆环，它几乎是完整的圆，上面只有一个极小的针孔。而在这两种极端情况之间，是一系列大小在它们中间的垫圈。

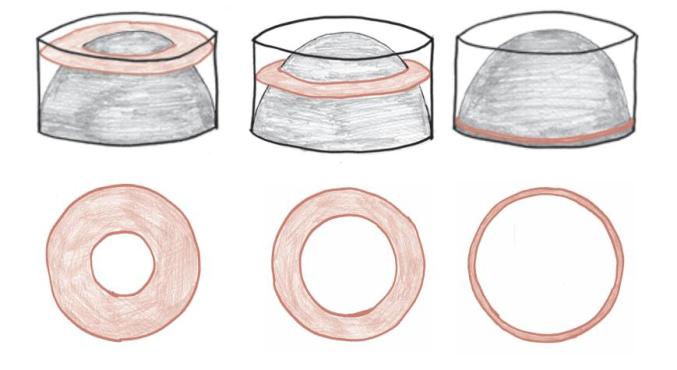
这些圆环的面积是多少呢？通过结合代数运算，我们可以推导出每个圆环的面积都是πh⊃2; ，其中h是它到地面的距离。

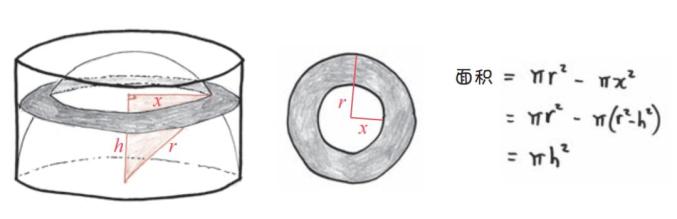
这就意味着借助“无穷灾难原则”，每一个圆环都可以用一个半径为h 的圆来代替。

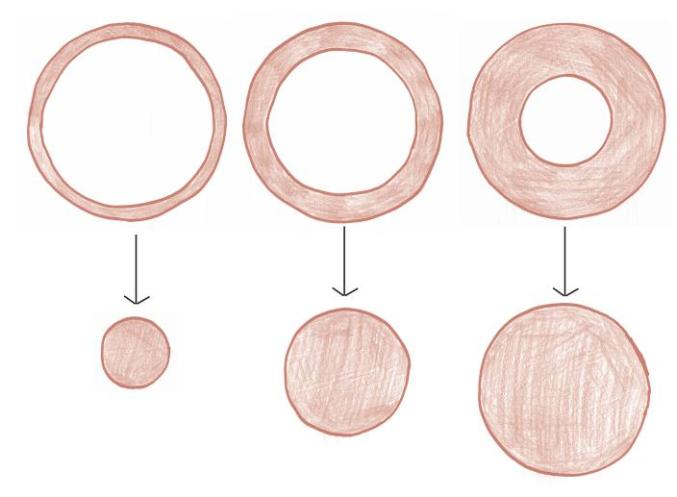
看！将它们一个个叠起来后，我们得到的不再是那个怪异的半球状火山坑，而是一个颠倒的圆锥。

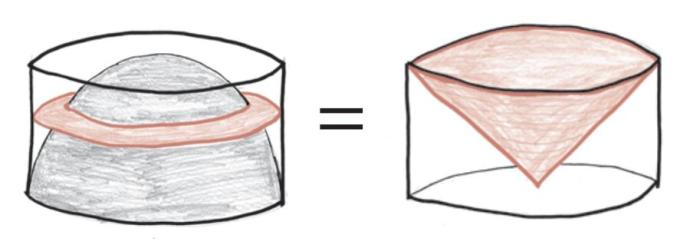
我们已经知道，圆锥体的体积是圆柱体的1/3。因此，空的空间——过 去是半球的那部分——占了圆柱体体积的2/3。所以得出结论：球的体积为圆柱体的2/3。

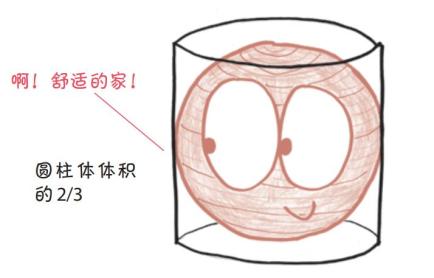
有了西西里沙地上的这些图形，阿基米德憧憬着几千年以后才会出现的积分。面积和体积、无数个切片、连续性和曲率问题的解决……这些是 积分的化学原料、原始汤剂，而后来的积分正是由此发展而来。那么，为什么全世界等待了这么久，微积分才诞生？

那一天，罗马军队终于攻破了这座城市。不过是短短几个小时，锡拉库萨就被烧毁了，士兵们疯狂地抢劫和杀戮。

历史学家李维（Livy）写道：“许多暴行都是在头脑发热和贪得无厌中犯下的。”即便如此，罗马军队的领袖马塞勒斯还是认为这位伟大的几何学家本应在这场战争中幸免于难。另一位历史学家则说：“他拯救阿基米德的功劳几乎和摧毁叙拉古（如今称 为锡拉库萨）的军功一样大。”

阿基米德甚至都没有注意到这座城市的沦陷。对他来说，与沙地上引人入胜的图形相比，战争中的掠夺和破坏又算得了什么呢？

阿基米德在面对凶神恶煞的罗马士兵时，到底说了什么？历史学家们对此意见不一。也许他恳求道：“请不要破坏我的圆环。”也许他怒斥道：“站远点儿，伙计，离我的图形远点儿。”也许他当时用手挡着沙地上的图形，仿佛他的思想比生命更宝贵：“冲我的脑袋来，别碰我的图！”无论真实情况是哪个，大家都一致认为是那个士兵杀害了他。

他的血流淌在沙地上，流到了那些他用手指画的沟槽中。马塞勒斯将军坚持要为他举行一场体面的葬礼，并以礼物和恩惠来慰问阿基米德的亲属，但这也无法改变这个创造“无穷灾难原则”的人死了的事实。

今天，阿基米德最伟大的遗产不在于弹弓和阿基米德之爪，而在于几何学。他清晰的论点、他对无穷的把握，以及他已经非常接近微积分的成就。或许，如果再给他一点点外力的推动，他是不是就能到达微积分领域了？那样的话，微积分在地球上出现的时间会比现在早几千年吗？

想想数学家阿尔弗雷德·诺斯·怀特海德（Alfred North Whitehead）的证词：阿基米德死于一名罗马士兵之手，象征着世界发生了翻天覆地的变化：热爱抽象科学的希腊人在欧洲世界的领导地位被务实的罗马人所取代。

务实主义并没有错。嗯……或许，还真的有？19世纪英国首相本杰明·迪斯雷利（Benjamin Disraeli）将务实的人定义为“重蹈先人覆辙的人”。根据怀特黑德的说法，罗马人就是这样一个民族。在这个获胜的文明中，你找不到战败民族的想象火花。他们的所有进步都局限于工程师的一些小小的技术细节。他们没 有足够的梦想家……没有罗马人会因为专注于数学图表而丧命。

几个世纪后，当地的叙拉古人几乎已经忘记了阿基米德的遗产。古罗马著名政治家西塞罗（Cicero）在游历锡拉库萨时有心寻找阿基米德的坟墓，他发现它“隐藏在荆棘丛中”，“一根小柱子，就在灌木丛上方”。他从墓碑上的雕刻图案认出了它，正如阿基米德所要求的，有一个球体和一个圆柱体。

如今，坟墓早已经消失，但证据仍然刻在我们的想象中——那是一种比灰尘、血液或罗马人的手工石雕更持久的媒介。

原标题：《如果没有被罗马士兵杀死，阿基米德能发明微积分吗？》

阅读原文