掷骰子预测世界杯冠军？

本文由「Light科普坊」出品

撰稿：焦述铭（鹏城实验室）

审稿专家：李炜（中科院长春光机所）

在每届世界杯足球赛开幕之际，都会有各路大咖为大力神杯的最终归属“算上一卦”，其中也少不了科学家手中的数学模型。“一千个观众中就有一千个哈姆莱特”，十个不同模型就可能预测出十个不同冠军，像巴西队，阿根廷队，法国队都是被预测的夺冠热门。

对于即将到来的2022年卡塔尔世界杯，英国一位流行病学统计研究者Matthew Penn却更看好比利时队[1,2]，要知道比利时队在世界杯历史上还从来没进过决赛。但这哥们绝不是在“瞎说”，一来人家有自己基于数据的概率模型，二来这个模型曾经在2020年欧洲杯的预测中大放异彩，当时准确地预测了意大利和英格兰会分别是冠亚军，并且预测对了八强球队中的六个。

图1：比利时（红色）在 2018 年世界杯四分之一决赛中击败巴西
图源：Кирилл Венедиктов/维基共享资源

在11月15日，Nature杂志慕名采访了这位预测大神，并公布了他使用同一模型预测的本届世界杯结果，各队夺冠的可能性大小如下：

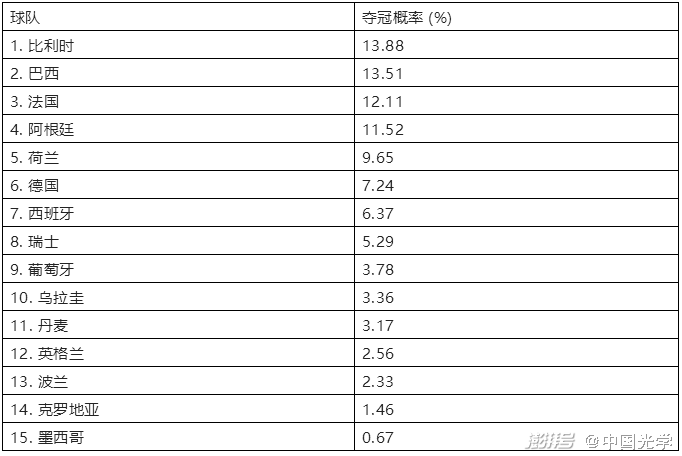
那么这些欧洲杯和世界杯的预测结果是怎么获得的呢？简单说是来自于每场比赛的掷骰子，却又不是简单的掷骰子，而是一种泊松概率分布。

我们投掷一枚普通骰子，会得到1点到6点中的任意一个，并且六种结果的可能性是相等的，称为均匀概率分布。而对于泊松概率分布，我们考虑这样一种情况：假设街边有一家生意并不怎么好的小店，每天经营10个小时，平均每天可以来30个顾客，那么平均每小时就只有3个顾客，还假设顾客都是随机选时间来的，并没有“客流高峰”，如果任意挑选其中营业的一个小时，来的顾客人数一定是3个吗？显然也不一定，这次碰巧可能一个人也没来，下次碰巧可能一下子来了十几个人。而法国数学家泊松给出了下面这一公式：

λ=3表示了平均值，P则表示了这一小时的时间段来了k个人的概率大小，e是自然常数。在泊松眼中，这家小店一小时内恰好来了3位顾客（平均水平）可能性是22.4%，而一个人没来的概率是4.98%，来了很多人的概率同样存在，但可能性很小，比如来了10个人的概率是0.08%，其它人数的概率也可以一一算出，像下图中所显示的那样。

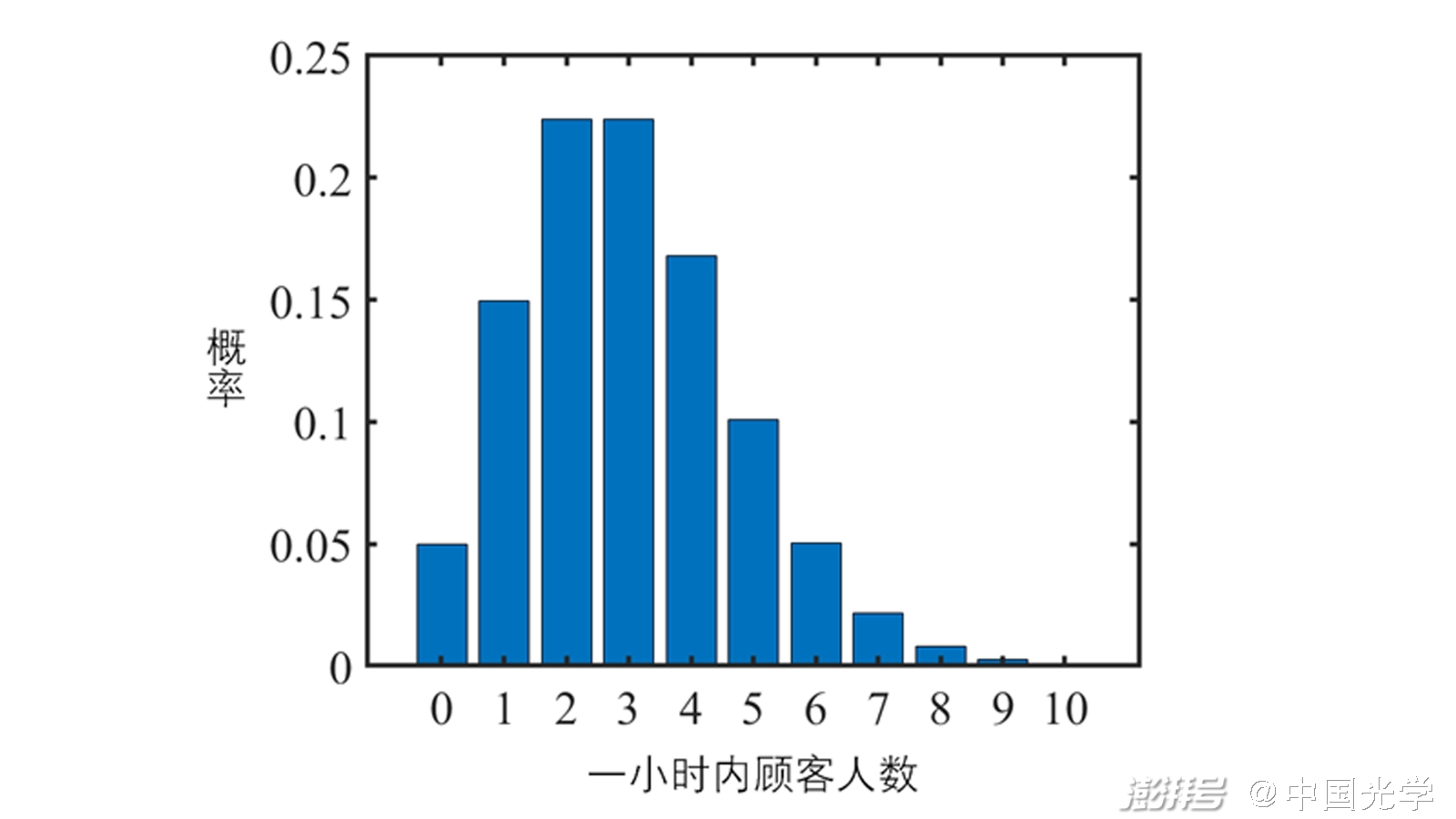
图2：平均值为3的泊松概率分布
图源：本文作者自制

在现实中，泊松概率分布其实无处不在，很多真实数据都和这一分布惊人的相似。其中包括了核物质每秒放射性衰变的次数，地震等自然灾害发生的次数，公共场所排队的人数，机器出现的故障数，每年飞机坠毁次数，某地区患病的人数，城市各区域犯罪案件发生数量，甚至是普法战争期间普鲁士士兵被马踢死的人数等等。

而在Matthew Penn的模型中，泊松概率分布用来表示了每场足球比赛中某一方的进球个数。一场比赛的胜负和比分自然同时取决于双方的实力和运气，确定性之中又充满了不确定性。

为了衡量各球队实力，模型中给每一支球队分别设置了“攻击力”和“防守脆弱性”指数，前者数值越高越容易进球，后者数值越高表示越容易丢球，防守力越弱。对此，各种网游桌游的玩家一定不会陌生，而在更遥远的时代，方便面里赠送的《水浒传》英雄卡上也都标记了每位好汉的攻击力和防御力。很显然，一等球队攻击力强，防守脆弱性低，二等球队攻击力弱，防守脆弱性低，或者反之，最差的一类球队攻击力弱，防守脆弱性高。

图3：干脆面袋里赠送的《水浒传》英雄卡
图源：赵阳（拍摄）/ Light科普坊

如果球队A和球队B比赛，按照“最合理最应该”的发挥，A队期待的进球数是A的攻击力乘以B的防守脆弱性，B队期待的进球数是B的攻击力乘以A的防守脆弱性。假设说A队攻击力是12，防守脆弱性是0.1，B队攻击力是6，防守脆弱性是0.2，两队的“正常”比分是2.4:0.6, 也就是约为2:1。但足球是圆的，我们只能认为2:1是最有可能比分，还有其它各种可能性，于是就将A队的进球数的不确定性看作一个以2.4为平均值的泊松概率分布，B队的看作是一个以0.6为平均值的泊松概率分布，各种可能比分的概率大小取决于两个进球数概率值的乘积。

当然一个最关键的问题还没有说，每个球队的攻击力和防守脆弱性的值大小到底怎么确定呢？答案是根据最近几年来各队之间的历史战绩，不断调整两个数值，使得预测的比分概率分布与实际记录的统计分布尽可能吻合。这样，在世界杯上任何两支球队之间交手时，各种比分出现的可能性都已经事先可以大致预测出来，模拟整个赛程，最后确定世界杯各队的夺冠概率也就成为了可能。

泊松概率分布在光学领域也是个“常客”，不过更是个经常制造麻烦的“刺头”。概率的不确定性给足球比赛带来的是惊喜，悬念和刺激，给光学成像带来的更多是带来难以忍受的捣乱噪声信号。

一束光可以看作是由很多个微小光子组成的，均匀照亮一张白纸后，看似纸上各处强度都很一致，但实际上纸的每个位置反射的光子数量会各不相同，而光子数量的多少也对应着光照明暗的差异。即使同一位置，不同时刻反射的光子数量也会不断有涨落起伏，都遵循着泊松概率分布。

对于相机来说，每次落到传感器上的光子数分布同样具有泊松概率的不确定性，不可避免引入了散粒噪声[3](图4左)，并且几乎无论怎样完善地设计一款相机，都无法直接去除这种噪声。根据泊松概率分布公式，光子数相比于平均数量上下起伏的波动程度大小会随着光子数平均值的平方根增大而增大，但光子数平均值正比于想要接收信号的大小，所以当光强度变大（光子数增加）时，虽然散粒噪声在变大，信号与噪声的比例(信噪比)却也会变大，最后看到的图像整体还是会更清晰。

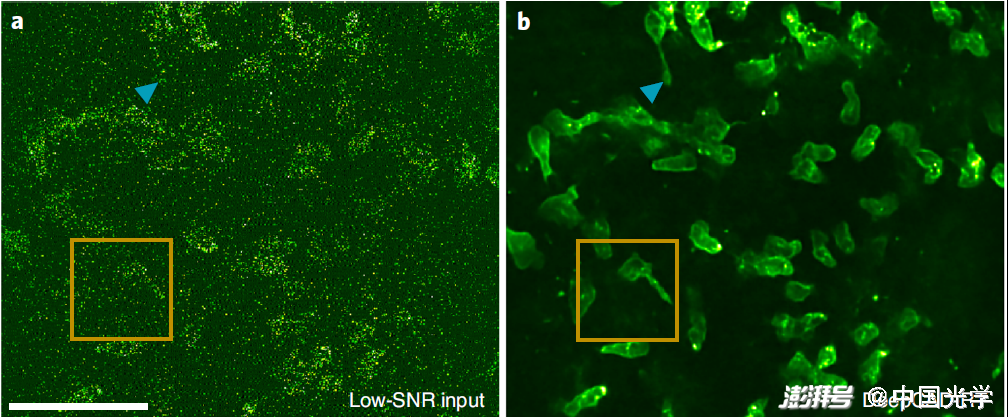
图4：荧光显微镜所观测的图像中散粒噪声(左)及人工智能算法处理后结果(右)[4]
图源： Nature Biotechnology (2022): 1-11.

然而在很多应用中，增加信号光的光子数或者强度是徒劳的，比如在户外使用无人自动驾驶汽车的激光雷达时，有时无论怎样增加激光雷达的光信号强度，比起太阳光都是“小巫见大巫”，此时去除噪声的一个办法是对没有任何目标物体的空白场景记录一次信号，作为背景噪声，之后每次记录时，都去掉这一静止不变的背景噪声。可是面对太阳光这一本身强度很大，又在以泊松概率分布不断动态变化的干扰信号，这一招也不灵验了。

而在使用X光的CT医学成像中，为了提升信噪比，加强X光照射强度也不可行，因为过量的X光剂量对人体是有害的。而即使在可见光的情况下，一些活细胞显微镜观测中，过亮的光照也足以杀死细胞，或者使细胞功能失常[4]。

2022年的诺贝尔物理学奖使得量子信息领域再次备受全球关注，其中相关的技术之一的量子保密通信可以提供理论上非常强的密钥安全性，但实际中需要满足的条件是拥有每次只生成单个光子的光源[5]，“一个也不能多，一个也不能少”，可实际中往往发射的一个激光脉冲中包含的光子数量本身也是泊松概率分布的，如果将平均值设为0.1个，有不少时候光源并没有发出光子，还会有少量时候发出两个或者更多个光子，这会使得量子通信系统没有理想中的那么高效和安全。

不过办法总比困难多，就像从混乱的进球数可能性中寻找到冠军球队的蛛丝马迹一样，面对神出鬼没的泊松概率分布噪声，研究者通过深度学习人工智能算法可以将拍到的照片中噪声完美去除，做到完好无缺的修复(图4右)。无论预测比赛比分，还是去除图片噪声，都离不开大数据作为参考，随机性的迷雾被异曲同工地层层拨开。

| 作者简介 |

焦述铭，鹏城实验室助理研究员，香港城市大学电子工程博士，从事全息三维显示算法，单像素成像，光学计算，图像处理，信息安全，机器学习等研究，曾获得香港特区政府Hong Kong PhD Fellowship Scheme和广东省“珠江人才计划”海外青年引进计划(博士后资助项目)。在Optics Letters, Optics Express, IEEE Transactions on Industrial Informatics, Engineering等期刊上以第一或通讯作者发表论文20余篇，获得2020年国际显示技术大会(ICDT 2020)优秀论文奖。担任《应用光学》和《液晶与显示》期刊青年编委，中国光学学会全息与光信息处理专业委员会委员，中国图像图形学学会三维成像与显示专业委员会委员，中国图像图形学学会三维视觉专业委员会委员。担任中国科普作家协会会员，Light科普坊科学家顾问团成员，曾在果壳网，科学大院，南方都市报，读者原创版等网络和平面媒体撰写科普文章，2013年第六版《十万个为什么》图书数学分册和电子信息分册作者之一。

本文封面图由Light科普坊提供

参考资料：

[1]Penn, Matthew J., and Christl A. Donnelly. "Analysis of a double Poisson model for predicting football results in Euro 2020." Plos one 17.5 (2022): e0268511.

[2]D. Adam, “Science and the World Cup: how big data is transforming football,” Nature 611, 444-446 (2022)

[3]https://en.wikipedia.org/wiki/Shot_noise

[4] Li, Xinyang, et al. "Real-time denoising enables high-sensitivity fluorescence time-lapse imaging beyond the shot-noise limit." Nature Biotechnology (2022): 1-11.

[5]Y. Hu, X. Peng, T. Li and H. Guo, “On the Poisson approximation to photon distribution for faint lasers,” Physics Letters A 367(3), 173-176 (2007).

阅读原文