处理双原子分子振动-转动热容量时的一个普遍性错误

原创 刘全慧 物理与工程

刘全慧教授

(湖南大学、物理与微电子科学学院、理论物理研究所)

即使大师笔法，拼凑在一起，也难成经典。

——题记

摘要

作为一个数学定理，能量均分定理无疑是正确的。但是，通常教科书用能量均分定理讨论双原子分子中的振动自由度，所得的摩尔热容量的结果却是错误的。究其原因，双原子分子中的振动和转动无法分离，当温度较高的时候，双原子分子理想气体的摩尔热容量在

有个小平台，然后以

作为渐近值，在

处不出现平台及其它特异性。

一、文献对双原子分子转动-振动热容量的通常处理

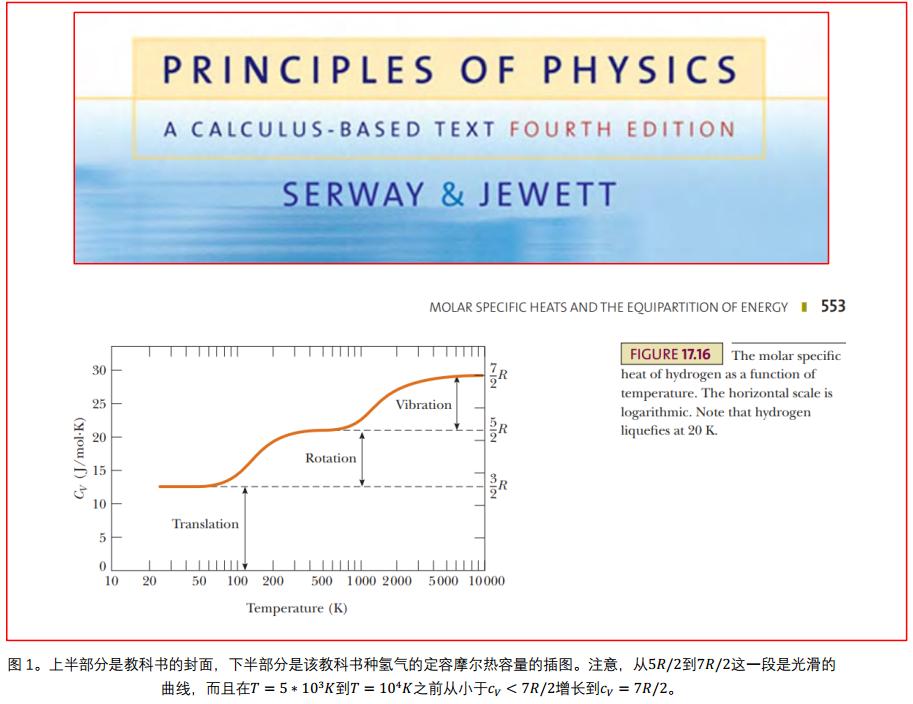
理想气体是热物理必不可少的内容，教科书中一般是首先处理单原子分子理想气体，然后是双原子分子理想气体，再根据教学需要逐渐引入更加复杂分子。当把能量均分定理应用到双原子分子理想气体时，气体的定容摩尔热容量为，

（1）

其中

分别为分子的平动、转动和振动自由度的个数。当然，能量均分定理并不完全正确。根据量子力学，较低的温度下转动自由度和振动自由度处于冻结状态，对热容量没有贡献。随着温度的升高，首先是转动自由度被激发，然后是振动自由度被激发。当全部自由度被激发的时候，定容摩尔热容量达到极大值，

（2）

把双原子分子热容量的全部可能数值和其温度区间图示出来，就是图1。这种表述也常见于我国热学教材或者大学物理教材中热学部分。

可惜的是，结果(1)(2)及图1，都认为

出现一个平台，这是不对的。根本原因在于：双原子分子转动和振动这两个运动耦合在一起无法分离，能量均分定理不适用。这个时候，即使在满足经典极限条件，也必须从玻尔兹曼统计从头计算。

接下来的第二部分将通过解析能量均分定理的证明过程，说明该定理成立的一个关键条件是不同自由度之间的运动不能出现耦合。第三部分双原子分子的振动-转动耦合及其对热容量的贡献的正确结果。第四部分是讨论和结论。第五部分是感悟。

二、能量均分定理成立的一个关键条件

最方便的讨论是从广义能量均分定理开始。以

表示玻耳兹曼系统中粒子的能量，则

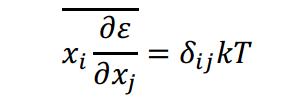
（3）

其中

分别是

个广义坐标和动量中的任意一个。 这就是广义能量均分定理。证明过程如下。

利用玻耳兹曼统计对统计平均值的定义，有

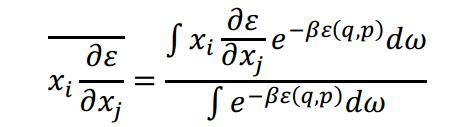
（4）

式中

空间的体积元。令

且

是除

外的其余

个广义坐标和广义动量的微分。式(4)可改写为

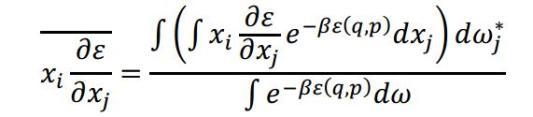
（5）

对其中的

进行分部积分，得

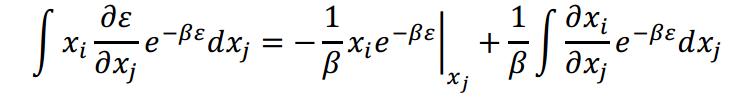
（6）

如果式右边第一项为零，再考虑到

，即有

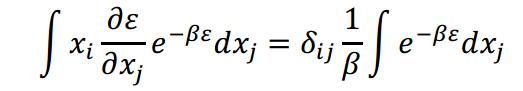
（7）

代回(5)式即得(3)式。于是广义能量均分定理得证。

假如

中含有

的项可以表为平方项，例如

（8）

其中

是

中不含

的部分且

为正常数，利用式立即得，

（9）

这就是通常的能量均分定理。

假如

中含有

的项可以表为平方项之外，还有其它部分包含在

中，即

（10）

利用式得，

（11）

立即发现，通常的能量均分定理不再成立。

因此，能量均分定理成立的一个关键条件是：分子能量表示式中的每一个平方项，只能出现一个自由度变量。如果某一个平方项中出现了不同的自由度变量，相应的不同运动间出现了耦合或者相互作用，这个平方项对摩尔定容量的贡献就不再是

。

三、双原子分子的振动-转动耦合及其对热容量的贡献

对于双原子分子，如果振动自由度被冻结了，能量表达式是

（12）

其中

为质心质量，

为约化质量，

为质心平动动能，是三个平方项的简写形式。这个时候，平动和转动这两个运动之间没有耦合，当温度足够高的时候，

（13）

如果振动自由度被激发，去掉质心平动动能，能量表达式是，

（14）

根据第二节的讨论，式中第一二两项出现了两个不同自由度的耦合，即刻画振动自由度的

和刻画转动自由度的

出现了相互作用，通常的能量均分定理不再成立。为了研究振动自由度的势能部分对能量均分定理的影响，下面计算平均值

（15）

即

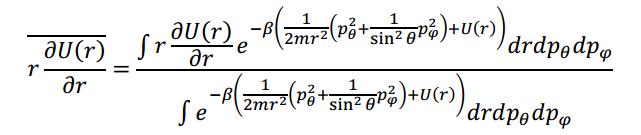
（16）

简化这个表达式，可得

（17）

如果

，立即得

（18）

这将和能量均分定理给出的数值

相差甚远。

如果势能有个平衡点

，下面计算平均值

（19）

即

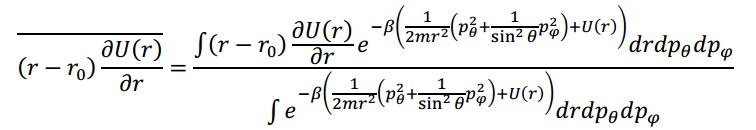
（20）

简化这个表达式，得

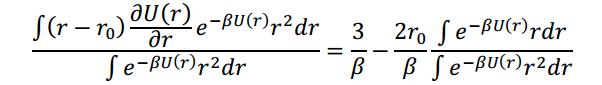
（21）

其中利用到了

，最后得，

（22）

取

（23）

立即得：

（24）

这个结果在两个极限下可以简化。低温极限下即

较大，

，（24）式给出

（25）

此时回到了通常的能量均分定理。但是，温度太低，振动自由度被冻结，这个结果其实不会出现。也就是，低温极限下，能量均分定理不适用于双原子分子的振动自由度的势能部分。高温极限时，

的变化范围较大，

，式给出

（26）

也就是，高温极限下，能量均分定理也不适用于双原子分子的振动自由度的势能部分。从可知，在双原子分子离解之前，不会出现

平台，而是在经过

之后，以

（27）

作为渐近数值，即图2所示的情况。

四、讨论和结论

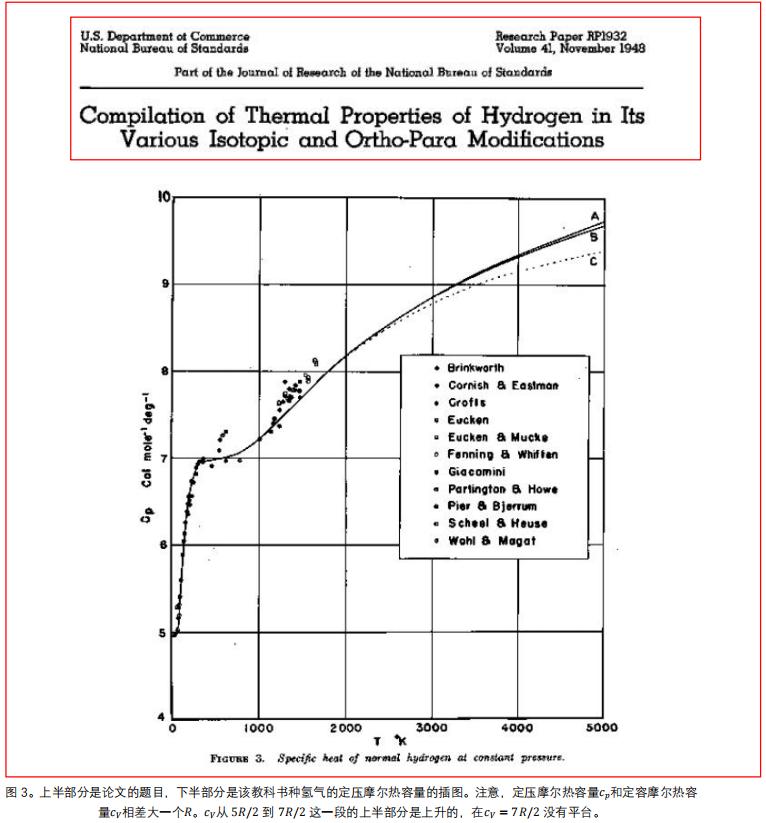
作为一个数学定理，能量均分定理无疑是正确的。一个典型的应用是，如果振动发生在固体的晶格点阵上，能量均分定理可以解释杜隆-珀蒂定律。但是，任何数学定理都有其适用范围。通常教科书用能量均分定理讨论双原子分子中的振动自由度，所得的摩尔热容量的结果却是错误的。究其原因，双原子分子中的振动和转动无法分离，当温度较高的时候，双原子分子理想气体的摩尔热容量在

有个小平台，然后

以作为渐近值，在

处不出现平台及其它特异性，参见实验曲线，图3。

五、感悟

所谓真理，是理论的真实。所谓实验结果，只是现象，现象不是真理。没有理论，实验数据可以出现相互矛盾的解释。

图2中接近

的部分之所以是错误的，是因为和理论不符合，当然也不可能和实验相符。教科书中不必采用实验曲线图3而是理论曲线图2。教科书也可以采用折衷处理，即把摩尔热容量接近

的部分画成虚线。

鸣谢：

湖南大学应用物理专业2018级的吴晓毅同学课堂上提出的一个问题并给出了初步结果， 2020级赵宇航同学也进行了一些计算并和我死磕了好一阵。就这个问题，和我的博士同学、南京大学鞠国兴教授之间展开了激烈的争论，他提供了很多文献和思路；我也曾把这个问题的初步形式放在全国热力学与统计物理教学研究会的微信群里讨论过，很多老师贡献了宝贵的思想。感谢诸位！也感谢每一位关心过这个问题的同学和老师！

刘全慧教授其他文章：

懂几何者,在物理学中无往而不利明天开始，刘全慧教授讲授狭义相对论(共四次，每次约两个小时)END

更多精彩文章请点击下面“蓝字”标题查看：

对麦克斯韦方程组拓展的评论王青教授：深入理解“拓展的麦克斯韦方程组”——2.0版王青教授：理解王中林院士“拓展的麦克斯韦方程组”“碰瓷”麦克斯韦：伽利略协变和洛伦兹协变电磁场论趣谈热点：运动介质洛伦兹协变电磁理论2021年《物理与工程》优秀论文、优秀审稿专家、优秀青年学者名单王青教授：源自苏格拉底的问题驱动式教育——在互动中共同学习和成长读后感：教育中的现实和远方王青教授：昨晚（6月9日），清华电动力学期末考试朱邦芬院士：“减负”误区及我国科学教育面临的挑战《物理与工程》2021年第6期目录乐永康：新冠肺炎疫情防控下美国物理实验教学及中美情况对比顾牡：对于重新制定的《非物理类理工学科大学物理课程教学基本要求》的认识和体会朱邦芬院士：从基础科学班到清华学堂物理班朱邦芬院士：对培养一流拔尖创新人才的思考李学潜教授：物理是一种文化李学潜教授：如何帮助物理系学生迈过从高三到大一这个坎穆良柱：物理课程思政教育的核心是科学认知能力培养穆良柱：什么是物理及物理文化？穆良柱：什么是ETA物理认知模型穆良柱：什么是ETA物理教学法吴国祯教授：我的国外研究生经历印象——应清华大学物理系“基科班20年·学堂班10年纪念活动”而写

陈佳洱，赵凯华，王殖东：面向21世纪，急待重建我国的工科物理教育王亚愚教授：清华物理系本科人才培养理念与实践葛惟昆教授：关于中外人才培养的几点思考安宇教授：为什么传统的课堂讲授模式需要改变安宇教授：其实教学就是积累的过程刘玉鑫教授：关于本科生物理基础课程教学和教材编著的一些思考沈乾若：重创理科教育的美加课程改革Henderson C：美国研究基金支持下的物理教育研究及其对高等物理教育的影响《物理与工程》期刊是专注于物理教育教学研究的学术期刊，是中国科技核心期刊，1981年创刊，欢迎踊跃投稿，期刊投审稿采编平台：

http://gkwl.cbpt.cnki.net

欢迎关注

《物理与工程》微信公众号

原标题：《处理双原子分子振动-转动热容量时的一个普遍性错误》

阅读原文