从全球数学发达中心的迁移看“数学文化与数学强国”

·“历史上数学发达中心的迁移，同社会政治、经济重心的迁移基本是吻合的。”如果未来各行各业都有更多人热爱数学，以讨论数学、研究数学为乐趣，那时我们国家的数学实力一定很强盛。

第一部分：数学强国及其启示

1、从ICM看数学强国

如何看当今有哪些数学强国，一个参考标准就是菲尔兹奖的获奖情况。

四年一度的国际数学家大会（ICM）已经正式落幕。今年，法国、美国、英国、乌克兰各一人获得菲尔兹奖。一个国家获得菲尔兹奖的情况可以很好地反映其数学实力。

图1：2022年菲尔兹奖得主（从左至右）：Hugo Duminil-Copin，许埈珥，James Maynard，Maryna Viazovska
来源：ICM官网/Matteo Fieni/Lance Murphey/Ryan Cowan/Matteo Fieni

从国籍的角度统计，菲尔兹奖获奖国籍-人数柱状图如下。蓝色代表的是获奖累计总人数，深红色代表的是其中外裔的人数。从图中不难看出前四名：美国19人、法国13人、英国8人、俄罗斯5人；美、法、英、俄四国在人数上，占据“大半个江山”；如果把俄罗斯和苏联作为一个“泛俄地区”，累计8人。而曾经同是世界数学中心的法国和德国，法国依然强劲，德国就显得有些没落。

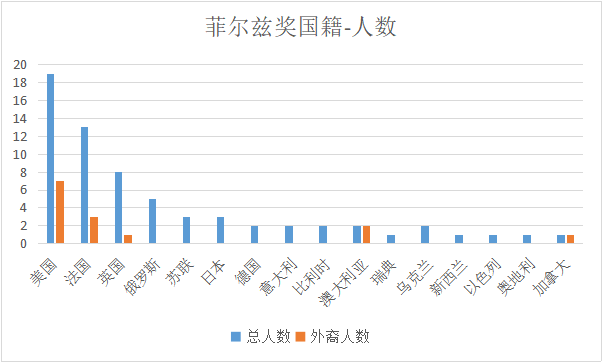
图2：历届菲尔兹奖统计情况（1936-2022）

菲尔兹设立菲尔兹奖的最初目的，就是为促进北美的数学发展。因为历史原因，二战之后美国数学崛起，德国走向没落。从图中也不难发现，美国、法国、英国作为三强，同时也是外裔获奖最多的国家。主要因为早期德国的屠杀、战败导致人才流失；苏联解体，导致人才流失；欠发达、不稳定国家和地区的人才流失。这些人才大部分流向了美国、法国和英国。为什么美、法、英、俄、德能成为数学强国？我们可以从历史中寻找答案。

2、历史上数学中心的迁移

张恭庆院士讲，“数学实力往往影响着国家实力，世界强国必然是数学强国”。李文林教授也说过，“历史上数学发达中心的迁移，同社会政治、经济重心的迁移基本是吻合的”[1]。

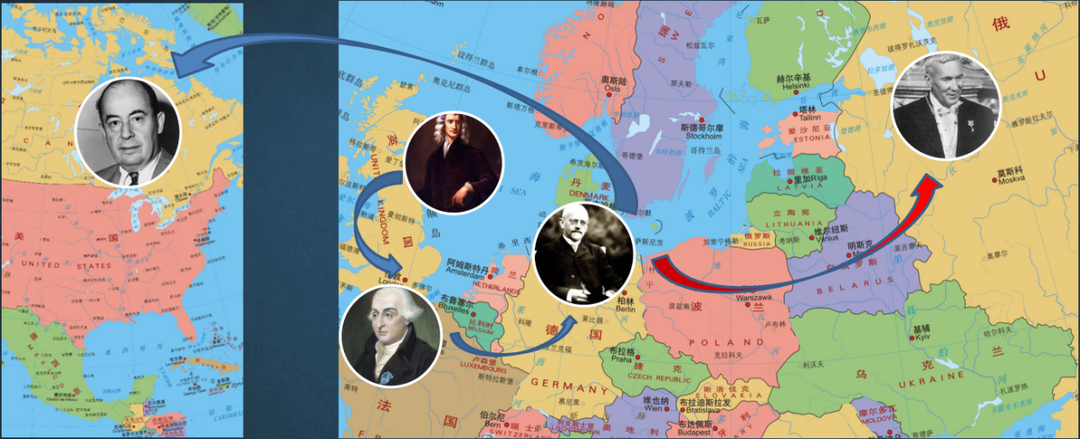
图3：近代数学史上数学发达中心的迁移

从15世纪开始数学活动的中心由于资本主义的兴起又返移欧洲，并随着资产阶级革命重心的转移而在欧洲内部不同的国家之间转移着：

·英国的资产阶级革命带来了它的海上霸权，同时也造就了牛顿学派、皇家学会的诞生；

·通过18世纪的法国大革命，法国数学取代英国而雄踞欧洲之首，巴黎在相当长一段时间内成为名副其实的“数学活动的蜂巢”；

·法国维持其数学优势直到19世纪后期，70年代以后，德国的统一运动又使德国数学起而夺魁，最终哥廷根成为全世界数学家向往的“麦加”；

·德国数学家的黄金年代，由于希特勒法西斯的浩劫而一蹶不振，二战后，美国便成为西方数学家的一片乐土了。

·苏联数学在二战前后发展十分强劲，在20世纪培育了上百位数学家，其中莫斯科大学成为诞生数学家的摇篮。

总的来说，数学的发展满足当时资本主义制度在政治、经济、军事等发展的需要。政治上，当时欧洲经历了漫长黑暗的中世纪，数学的发展在推动着自然科学进步的同时，也作为一种革命动力，加入了冲破宗教束缚的战车，有助于人们思想的解放，进一步加强资本主义制度的确立和巩固；经济上，由于各个资产阶级国家陆续开展了工业革命，数学的发展也直接或间接促进当时生产力的发展；军事上，西欧各国发展的不平衡加剧了各国之间利益矛盾而引发的战争，再加上海外殖民，需要大力发展数学来满足军事需要。这里对于苏联的社会主义制度同样适用。

3、高度重视大学数学教育和人才培养

（1）德国篇——哥廷根大学

哥廷根大学几乎培养了全球的数学家。而克莱因是哥廷根大学的实际掌舵人，也是一位帅才型数学家。

克莱因的声望吸引着世界各国，特别是美国的学生。一位英国青年向剑桥的朋友报告哥廷根数学系的情况时写道：“我们这里的国籍很杂，五个美国人，一个瑞士籍法国人，一个匈牙利人，一个意大利人，其余少数几个则有德国血统。”[2] 下面主要从三方面讲一下克莱因的数学教育。

重视教学

授课。克莱因教学极为出色，是教师们学习的好榜样。他编写的讲义，不仅文字流畅、条理清晰，而且结构严谨，对读者有很大的吸引力。上课之前他总是做充分准备，同时对讲稿中思路不清、表述不足的地方进行加工、修改，并对教材内容、数学公式、图表和引文等进行周密的安排，做到胸有成竹、一丝不苟。

克莱因讲课时，思路清晰，重点突出。他认为学生应当自己思考、分析，去完成定理的证明。学生要想掌握课堂上讲授的全部内容，课后还需要认真地复习、翻阅参考书和完成作业等，这样往往要再花几倍的时间。他的这种教学方式有效地培养了学生的自学能力以及分析问题和解决问题的能力。

克莱因很讲究板书，他在讲课过程中的板书从不马上擦掉，最后便形成讲课内容的一个完好的概括。他把每一个问题都写得恰如其位、井井有条，给人以美的感受。

重视讨论班。克莱因很重视讨论班的教学方式。他认为这种方式可以培养学生的自觉学习能力和激发学生学术研究的兴趣。他常把自己正在研究中的问题提到讨论班上来，同时把解决问题的思路介绍给学生；有时还让学生在黑板上讲解所学的论著，然后让大家提出问题进行讨论。

散步。数学系的大小事情是在每星期四下午三点的数学散步中解决的。这种散步是非正式的课程，系里的教学人员、学生都可参加。散步过程中以谈论数学问题为主，当然也包括一些系里其它的事务。

教师要求。克莱因还认为教师应具有较高的数学观点，他认为在数学中讲点数学史是必要的。

广揽人才

他广揽人才，建立实力雄厚的数学教授班子，例如希尔伯特、闵可夫斯基、诺特、外尔等大家，振兴哥廷根数学学派。

数学教改

他大力推动数学教改，基础数学与应用数学并重，并将教改推广到全德国，培养出一大批科学与技术兼通、既有深邃眼光又能解决实际问题的人才。他还大力提倡应用数学，创建了哥廷根应用数学学派。结果哥廷根在应用数学研究方面很快就跑在世界的前列。后来有些国家群起效仿，相继跟上。与此同时，他竭力促进数学、力学和其他基础学科在工程技术中的应用，并在哥廷根大学成立了应用力学系，推动了应用力学的发展。克莱因慧眼识珠，引进普朗特，哥廷根应用力学学派从此发扬光大。

（2）俄罗斯篇——莫斯科大学

俄罗斯数学从19世纪开始崛起，到了20世纪前苏联时期成为世界数学强国之一。特别是苏联于1958年成功发射了第一颗人造地球卫星，震撼了全世界。当时美国总统约翰·肯尼迪决心要在空间技术上赶超苏联。他了解到：苏联成功发射卫星的原因之一，是苏联在与此相关的数学领域处于世界的领先地位；此外，苏联重视基础科学教育（包含数学教育）也是它在基础科学研究中具有雄厚实力的一个重要原因。因此肯尼迪下令大力发展数学。

苏联科学家的论文大多都是以俄文发表的。而美国数学会、伦敦数学会联合起来，将俄国几乎所有的知名综合数学杂志以及众多的专业数学杂志一字不漏地全部翻译成英文。大量的苏联教科书被翻译成英文等多种文字在全世界发行并应用，也说明了人们对前苏联教育、科研体系的认可。直到今天，美国很多出色的数学培训机构都参考了前苏联那套体系。

纵观整个20世纪的数学史，苏俄数学无疑是一支令人瞩目的力量。百年来，苏俄涌现了上百位世界一流的数学家，而这些优秀数学家则大多毕业于莫斯科大学。

师徒传承：叶戈洛夫—鲁金—柯尔莫哥洛夫—盖尔范德

叶戈洛夫讨论班最大的成果是收获了数学大师鲁金。此人是那种承前启后的人物，本身又是实分析的大师，编写了一些经典教科书，同时又培养了诸多大师，大名鼎鼎的柯尔莫哥洛夫就是其中之一。在柯尔莫哥洛夫时代，莫斯科学派迎来它的巅峰时刻。

图4：柯尔莫哥洛夫

柯尔莫哥洛夫是一位伟大的教师，受他影响的数学家已不计其数。直接受他指导的学生数目也是十分惊人，恐怕是一个难以逾越的记录：67。其中成为苏联科学院院士的就有14人。

1932年，没有读完高中、未上过大学的盖尔范德被莫斯科大学破格录取为研究生，师从柯尔莫哥洛夫。

图5：盖尔范德

1943年起，盖尔范德在莫斯科大学组织自己的数学讨论班。他把讨论班办成了选拔合作者及培养数学新秀的中心，最终讨论班发展成为闻名全球的“盖尔范德数学讨论班”，该讨论班一直坚持到盖尔范德1990年移居美国。此后，他把讨论班这个传统也带到了罗格斯大学。

高级讨论班

举行高级数学专题公开讨论班发挥了关键作用，这在莫斯科大学习以为常。这些讨论班向所有人开放——从有才华的高中生到被禁止进入官方机构的学者，促进了代际和机构间的联系，凝聚了人心。这些公开讨论班中规模最大、最负盛名的当属盖尔范德讨论班。不少数学家的回忆录记录其盛况时“大概得有两三百人参加”。

4、放眼全国：极其关注中小学数学教育

这里还是以德国的克莱因和俄罗斯的柯尔莫哥洛夫作为主要代表。

（1）德国篇——克莱因

组织科学教育改革和普及数学知识。克莱因亲自参与制定、改进和扩大德国中学科学教育的计划；提倡第一流数学家向非数学专家作通俗讲演；组织编纂三十卷的数学辞典，以提高全社会的科学与数学水平。

克莱因的主要著作有《高等几何学》、《非欧几何学》、《高观点下的初等数学》、《关于19世纪数学发展的讲义》等。此外还有《关于黎曼几何的代数函数论》、《20面体讲义》、《自守函数论讲义》等论文。尤其令人称赞的是他编纂的三十大卷数学辞典，给数学教育工作者带来很大的方便。

（2）俄罗斯篇——柯尔莫哥洛夫

柯尔莫哥洛夫一向重视数学教育。为培养优异的少年数理人才，他开办了数学物理寄宿学校（人称柯尔莫哥洛夫学校）。他晚年从事中学数学教育改革，力图提高整个苏联的数学教育水准。他为此举办讨论班，编写教材，组织试验，亲自到中学讲几何课，耗费了无数的心血。

我们可以思考一个问题，为什么外国有那么多年轻的数学家呢？就是它长期以来，数学文化发达。一个民族的多数人从小就知道数学是怎么回事，就琢磨数学、理解数学，他就能够早一些出成果，成为数学家。

第二部分：愿景：未来中国的数学文化

今天，宿迁学院的李红铃老师在讲课中引用了顾沛老师关于“数学文化”的定义，听完很有启发。数学文化不仅包含数学的思想、精神、方法、观点、语言，以及它们的形成和发展，还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等等。

这里，我想从另一角度解读数学文化。我认为我们还需要关注国家或社会是否具备有利于数学发展的文化环境。例如我们都知道巴西的足球文化盛行，这不仅仅是因为他们足球踢得很厉害，还与足球氛围有关。在巴西，足球真正成为一种全民运动的游戏。在巴西的街头巷尾，不论是在城市还是在贫民窟，随处可见足球的身影。目前我们国家的麻将、象棋的普及程度相当高，总能在街头巷尾看见对弈和围观，但是我国对数学有兴趣的人太少了。如果有一天，我们随便在大街上找一个老太太都能侃上两句数学，那我们一定能建成数学强国。

接下来，我主要从五方面谈谈关于未来中国数学文化的愿景。

1、数学名家、科研人员更加重视数学教育

数学家也可以是数学教育家，而数学教育包括大学数学教育、中小学数学教育以及面向全社会的数学科普教育。自古以来，有诸多数学家将数学教育放在重要的位置。在20世纪初，德国数学家克莱因倡导以“函数为纲”的数学教育改革运动，英国数学家贝利制定了实用数学教学大纲，法国数学家阿达玛和勒贝格等编写数学教科书，美国数学家摩尔提倡混合数学，日本数学家小平邦彦和广中平佑在上世纪60年代对“新数运动”的批判，我国的华罗庚等对数学教育的关心……这些历史案例展现了数学家与数学教育的密切关系。数学家由于其特殊地位，在数学教育的发展过程中发挥着至关重要的作用。

新中国成立后，出现过“精英教材”的时代，诸多著名专家、学者、教授进行教材的编撰，甚至华罗庚这样的超级专家带队编写中小学数学教材。近年来，在我国也有不少数学家关注、参与数学教育改革及数学课程标准的制定工作。例如张景中院士的“从数学教育到教育数学”、王梓坤院士和徐利治教授的“MM 教育方式”（运用数学方法论的观点来指导数学教学），袁亚湘院士等大力推动数学科普教育工作。他们对数学教育的关注令数学教育工作者欢欣鼓舞。目前在数学科普层面，较好的科普平台并不多。中科院物理所微信公众号的科普做得很好，结合现实又蕴含丰富的物理知识，值得数学领域借鉴。

希望未来有更多的数学大家关注数学教育，对于数学的发展、数学学习的规律和次第有更深刻的把握，并用以指导学生。这将有利于培养出具备数学素养的学生，提高整个数学领域的研究水平。

2、数学科普作品类型更丰富、质量更高

目前，我国每年数学科普图书的出版数量已经非常可观，但是在其他方面还有比较大的进步空间。比如体量不小，但影响范围有限，县乡的中小学生很少接触；内容上侧重于初等数学，而关于高等数学的科普少，受众窄；现在也比较缺乏年轻有为的数学科普作家。

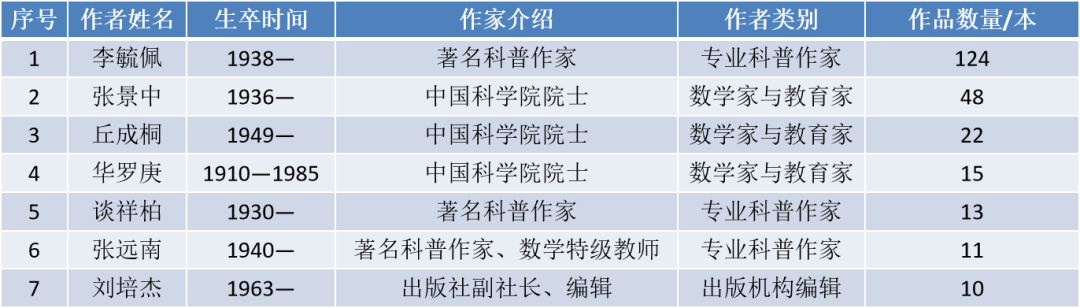
图6：出版数量超过10本的数学科普核心作者情况
来源：《新中国成立以来数学科普图书发展研究：基于丛书的分析》2021年

我们现在非常需要年轻的数学科普作家，当然参会的很多老师都有非常多优秀的作品，也希望未来能涌现更多的数学科普创作人才。

3、高校数学社团蓬勃发展

北京很多高校都有数学类社团，我认为数学社团能发挥的作用很大，它对于提高学生数学兴趣、了解数学史、学习数学思想上都很有帮助。我认为好的数学社团，它的活动可以主要包括这四个方面：日常答疑、考前辅导、竞赛培训等；举办大型数学讲座；拜访数学老教授；组织学习讨论数学思想和数学史。

我在本科期间有过3年的社团经历。当时社团每年都建设规模近两千的数学交流群，不仅面向全校学生进行数学答疑，还在学生当中建立一个高数讲师团进行考试复习答疑。我们社团还邀请到李尚志教授、林群院士和严加安院士到学校开展讲座，这是大学平台的一个优势。另外社团还组织成员每周学习讨论数学科普，如《数学史概论》和《微积分的历程》。

如今，我们“数学经纬网”也已经和不少学校的数学社团合作承办讲座，将一些名校名师的课程推广到其他学校和广大网友。高校数学社团是一个传播数学文化的非常好的实践平台，我们也希望未来的高校数学社团能够蓬勃发展。

4、大众了解数学、热爱数学、研究数学

我国很多人在谈及数学研究时，热衷于把陈景润的“1+2”挂在嘴边，却很少有人了解其具体含义。这一方面反映了四十多年前报告文学《哥德巴赫猜想》的影响力之大之久，另一方面也反映出与数学成果宣传相对应的数学思想普及程度不足。

图7：徐迟《哥德巴赫猜想》（左图），1742年哥德巴赫给欧拉的信函（右图）

我国目前进入到“全民奥数时代”。今年是中国队在国际数学奥林匹克竞赛（IMO）中第23次获得世界第一。自1985年中国首次参加奥赛以来，这30余年间，我国参赛选手共获得174枚金牌，平均单次参赛可获金牌数为4.7枚，这些数据都是世界第一。然而菲尔兹奖获得者却0人。可以说，中国有数学天分的学生很多，但是这些学生是否都发自内心热爱数学、对数学研究充满乐趣，以及未来在数学道路上能走多远，是一个值得数学教育界深入思考的问题。

图8：全民奥数时代

在中国的街头巷尾，凡有棋局必有围观，大家都喜欢琢磨讨论。而在英国会有一种现象，其貌不扬的老奶奶也讨论数学问题。之前我们与中科院数学与系统科学研究院的李文林老师有过当面的交流，他讲在英国咖啡厅遇到的一位老太太，听说他是学数学的，非常激动，向他聊起了自己中学时学数学的情景。在上午的报告中，田刚院士就介绍了一位家庭主妇玛乔丽解决五边形密铺的问题。美国数学会总部装修时，新地板就采用了玛乔丽发现的五边形密铺。可见，在国外数学也是非常“接地气”的科学，除数学家以外的普通人也乐于讨论、研究它。

5、未来可期：数学文化教育的相关政策

未来是可期的。近20年来，我们政府已陆续出台了有关数学文化教育的相关政策，足以表明国家对数学文化教育的不断重视。

2002年6月，我国正式颁布《中华人民共和国科学技术普及法》，是目前世界上唯一一部专门针对科普的国家法律。

2006年3月我国发布实施《全民科学素质行动计划纲要（2006—2010—2020）》，是新中国成立以来第一部有关提高全民科学素质的纲领性文件。

我国于2021年7月成立了中国数学会数学教育分会。

为加强对数学科普工作的引导，我国已于2021年7月成立了中国数学会数学教育分会。中国科协于2022年2月25日发布《中国科协2022年科普工作要点》，在其中提出了打造“省市县文明实践中心”联动的基层科普组织动员体系。数学教育分会的成立和基层科普组织动员体系的建立，表明了国家在提升全民科学素质特别是数学素养的决心和行动，这对于团结广大数学工作者，促进数学的发展，繁荣我国的科学技术事业具有重要的意义。

基础数学研究几乎不需要昂贵的仪器，而只需大脑和纸笔。如果未来各行各业都有更多人热爱数学，以讨论数学、研究数学为乐趣，那时我们国家的数学实力一定很强盛。

参考文献：

[1] 李文林. 数学史概论（第四版）[M]. 北京：高等教育出版社，2021.

[2] 张奠宙. 二十世纪数学经纬[M]. 上海：华东师范大学出版社，2002.

（作者王永涛，系北京航空航天大学的一名在读数学博士，在大学期间曾与同好们建立“数学经纬网”。本文系王永涛于2022年7月在河南开封举办的中国数学会第十一届全国数学文化论坛上作的报告，原题为《从数学文化看数学强国》。“澎湃科技”经数学经纬网授权刊发，略有删改。）