我在复旦学逻辑（四）

编者按：本期为“我在复旦学逻辑”系列的第四篇，我们邀请到了本科毕业生刘明君同学前来分享他在复旦与逻辑相处的时光。刘明君同学曾经选修了我们开设的数理逻辑学程，学习数理逻辑使他受益匪浅。数理逻辑学程结合了哲学学院、数学科学学院与计算机科学技术学院的优势学术资源，在与已有培养方案兼容、自由进出的前提下，为有兴趣的学生提供完备优质的数理逻辑培养计划。欢迎任何对逻辑感兴趣的同学报名参加数理逻辑学程。

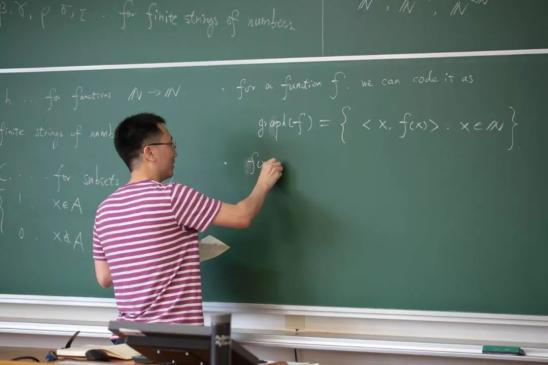
<<< 关于复旦逻辑的记忆 >>>

转眼我的大学四年生活就要过去，我也要离开复旦了。很高兴在这四年中遇到了数理逻辑学程，并且能在离开之前留下自己的一些回忆。

我和逻辑的缘分要从高中的时候开始说起。我高中的数学老师当时在教我一些离散数学，里面讲到了简单的基数，就让我对“无穷也可以比大小”这个事情非常好奇。在闲聊时，老师也和我聊起过他和逻辑的缘分，他在读大学时为了搞清楚哥德尔不完全性定理，专门去哲学系学了数理逻辑，这也为我去哲学系学数理逻辑埋下了伏笔。

还有一件丢人的事情，有一次老师讲了一个基数运算的题目，大概是说某个幂集和实数等势之类的。讲完做法之后老师说现在还没有不用选择公理证明的方法。虽然那时候我还说不出选择公理的具体内容，我还是起了兴趣，觉得就是想办法构造个函数说明双射就可以。我就回去想证明，下一周下课之后就和老师说，然后说着说着就发现自己的证明是错的，然后就回家继续想，反反复复我给了三四次伪证，但是老师都特别有耐心地听我胡说。到最后我觉得不能这样下去了，就不再乱想了。

选择公理（来自复旦集合论教材）

特别感谢老师的耐心，我从这件事里一个是学会了不要没事想着搞大新闻，第二就是让我对于如何确认一个证明是正确的有了兴趣。数学证明都是用自然语言写出来的，我们怎么可以判断证明里的一句话是不是真的可以从之前的论证中得到？正好当时还学到了Peano公理，学会了怎么构造自然数，就还想了解这种建立数学基础的工作。现在看来我倒是把数理逻辑学科开始的几个想做的事情都给集齐了。

来到复旦之后和逻辑的相遇更像巧合。刚入学的那几天，我闲得无聊翻看那本四五百页的培养手册，看有没有好玩的课。本来只是在看数学系的培养方案，考虑以后要不要选。因为真的没什么事做，我就一页一页把培养方案看到了最后，突然发现了数理逻辑学程的那一页，想起高中时候的事情，就决定要来学这个学程。但是第一个学期有个入学教育会，会上学院的老师特别警告说技科二十多学分的课程已经很满了，不要乱选课，会搞得自己挂科。我就没选第一学期的数理逻辑。

郝兆宽老师课后答疑

之后上谢锡麟老师的数分，碰到了一个存在性的命题，我又好奇这个东西是不是要用选择公理，谢老师说我得去哲学系问郝兆宽老师。当然我最后也没问过郝老师这个事情，其实这个问题也不是那么重要，只是我当时总是纠结于要避免选择公理云云。实际上完全没有必要去避免它，选择公理早就是广泛被接受的公理，研究选择公理的时候才需要想这种问题，平常需要找到一些东西就可以直接用选择公理就是了。

到第一学期其中的时候我感觉不对劲，数理逻辑这门课是整个学程的第一节课，并且只在秋季学期开，我这个学期不选数理逻辑，那我第二学期就选不了课。而且明年我还是要选各种专业课和通识课，又很可能和学程的课又时间冲突。我就赶紧买了数理逻辑的教材，开始自己看了起来。看到了学期末，我也大概把这本书前六章学完了，做好了下个学期开始正式选学程课的准备。但当时自己还是非常犯怵，害怕自己学的不对，记得好像还给杨睿之老师发过邮件问第二学期的课的难度。数理逻辑的教材名字是《数理逻辑——证明及其限度》，还有集合论的教材《集合论——对无穷概念的探索》。两本书的副标题起得特别好，直接指出了两本书的最终目标。

武丁教授2018复旦讲座现场

2018年秋季学期应该是逻辑学程最热闹的一个学期。复旦的学程工作刚刚开始，郝老师邀请到了很多老师来复旦线下开讲座。疫情之后再有大型活动只能线上参加了。最盛大的讲座是Woodin教授的讲座，借用了5301那个特别大的报告厅，当时我还什么都不懂，听了10分钟之后就开始掉线，只能看Woodin教授高兴地介绍他的终极L计划。当然我现在虽然学了这么多本科课程，也还是完全不懂终极L这些东西，或者说在讲座上能听懂著名学者做了几十年还没有做完的工作才是见了鬼，这也不是听讲座该有的期待。

第二个学期开始就算是正式进入了学程的学习。这个学期杨老师开了模态逻辑和可计算性理论。模态逻辑简单一些，学的内容大概就是一阶逻辑的一种推广。可计算性理论开始比较简单，后面就开始变难。有一个大定理，说的是五条图灵度和一阶句子的量词层级的关系，我就一直没有学会，甚至都死活记不住这几条结论。相比之下同样是计算机系的王飒学长就让人感觉在课下做足了功课，完全掌握了这个定理。但是之后杨老师带着我们“开火箭”，讲avoiding cone那些图灵度的偏序性质还是非常令人兴奋的，虽然只是学到了一些皮毛，也可以看出来图灵度构成了非常复杂的偏序结构。这些事情远远超出我们可以计算的范围，但是我们可以在数学的角度上证明这些性质。

杨睿之老师正在授课

这个学期姚宁远老师组织了伪有限结构的讨论班，也欢迎本科生来参加。我就又厚着脸皮报名了。到了光华楼2403之后发现一共只有几个人，本科生只有两三个人。姚老师讲课非常关心我们几个本科生有没有听懂，在第一次讨论班上花了很多时间来讲超积。这是我第一次听到超积的定义，完全不能在几十分钟里学会这个东西，后面利用超积构造的伪有限域的内容就更是完全跟不上思路。第二次课人就开始少了，我大概是第三四次开始接受了自己水平不到位的现实，开始不去的。现在感觉的话，姚老师特别好，愿意给我从头开始讲一遍，但是自己基础知识还不够扎实，又没在平常的时间多看看这个东西，还是趁早退出，学些不会打倒自己的东西好，也不要耽误讨论班的速度。

姚宁远老师的讲义

大二的时候又学了集合论和模型论。我集合论学得好些，学的东西和习题大多都能做出来，但也有一些麻烦的习题需要想比较长时间才能想到。我有个习惯是在吃饭散步之类的时间想事情，印象比较深的是有个题大概是要证存在和实数等势那么多个至多实数大小的线序，做法还是有些复杂，就一边想这个问题一边去春晖。吃完烧烤就大概想了个构造，赶紧回宿舍写了下来。没有什么特别的，就是单纯的做出题的快乐。模型论就难一些，而且因为不是学程的课，只有五个人选。我模型论其实学的很差，但是和学长学姐讨论还是感觉很有收获，特别是张体云学长，感觉他真的什么都会。

学程里面只要求选五门课，去掉数分、抽代之类数学系的课，大概会有三门左右是逻辑的课程，但是我大概是有收集的爱好，基本上对着几位老师开课的列表挨个学了一遍。但也只敢说是学了个皮毛，而且自己记性又不好，现在也只能说个大概。感谢几位老师为本科生准备了这么多课程，有些课程是在我入学之前老师们就一直开的，有些是后来才开起来的。但是老师们每年都坚持开课，没有因为选的人少就停掉。而且听说外系上课时间会有冲突之后，老师们也把一些课安排到晚上来方便大家选课。当然，复旦的课太多了，不管安排在什么时段都会和其他课冲突，外系的专业课也很可能是年年都和想上的课冲突。感觉就算老师们再怎么操作也没办法完全错开，而且有些课也是哲院的专业课，为了其他系的排课时间而到处调也非常不合适。只能说如果真的有想选的课的话，总是能挤出时间安排上的。

范畴论讨论班

第二年之后本科课差不多都学完了，但是自己比较懒，听集合论进阶的大基数又变得吃力，后来就没有参加后续的各种讨论班，主要是听了些感兴趣的报告和参加了一次暑期学校。说是听报告，实际上更像是追星。很多时候老师们讲得很清楚，我也觉得这个方向非常有趣，但是听过去也就过去了，没有专门选择哪个方向深入学习下去。后来还有周佳楠同学组织的范畴论讨论班，也让我了解到了不同视角下的逻辑和数学。

非常感谢郝老师组织逻辑学程还有几位老师的辛勤付出，祝数理逻辑学程越办越好！

原标题：《我在复旦学逻辑（四）》

阅读原文