你也能懂的质能方程E=mc²

提到爱因斯坦，很多人的第一反应就是E=mc²。

没办法，质能方程看起来“太简单”了：左边的E代表能量，右边的m代表质量，c是光速，都是中学生就能看懂的物理量。而且，这个方程看起来太神奇了，它告诉我们一般物体都蕴含了巨大的能量，原子弹那毁天灭地的力量就是最好的证明。

又简单又神奇，不传播你传播谁？

但是，很多人容易忘记一件事：质能方程是狭义相对论的结论，需要站在狭义相对论的立场上才能精准地把握它。否则就容易望文生义，再类比、推广一下，后果就很可怕了。

比如，有人认为质能方程的意思是“质量可以转化成能量”，或者说“物质可以转化成能量”。延伸一下，物质代表“有”，能量代表“无”，质能方程暗示着“有无相生”，接下来欢迎进入太极物理频道……

也有人认为质能方程是在说“质量是能量的一种形式”。延伸一下，我们的物质本质上都是能量，一切都是能量，一切都是虚无，色即是空，接下来欢迎进入相对论佛学频道……

这种误解以及可怕的延伸，我还可以列很多。要不是建了那么多社群，见识了各种各样的人，我真难以想象质能方程会有如此丰富的“内涵和外延”。

不过，想想也不奇怪。毕竟谁都可以谈一下质能方程，谈的人多了，想法自然就多了。而且，质量亏损这个名字也很容易把大家往歪路上引。

那么，我们就来好好看一看质能方程，看看E=mc²到底是怎么回事，看看它是如何从狭义相对论推导出来的，以及如何正确地对待质能方程。

01从狭义相对论出发

因为质能方程是狭义相对论的产物，所以，想搞清楚质能方程就得先搞清楚狭义相对论。

什么是狭义相对论呢？

我在《相对论诞生：爱因斯坦是如何创立狭义相对论的？| 主线》里详细描述了狭义相对论的诞生过程，看完文章的朋友肯定都知道：狭义相对论的核心是洛伦兹协变性。

它跟牛顿力学的核心区别是：狭义相对论的物理定律在洛伦兹变换下保持数学形式不变，而牛顿力学的物理定律在伽利略变换下保持数学形式不变。至于尺缩、钟慢、双生子之类的效应，都是狭义相对论的一些简单结论。

质能方程E=mc²也是这样。

也就是说，只要我们认为物理定律应该在洛伦兹变换下保持数学形式不变（狭义相对论精神），我们就能推出质能方程E=mc²，而不需要其它的假设和限制。

因此，只要狭义相对论成立，质能方程就成立，它的适用范围是极广的。有些朋友认为质能方程只在核反应里才有效，这显然不对，因为狭义相对论并不是只在核反应里才有效。

那狭义相对论在哪些地方成立呢？是不是像有些人认为的，狭义相对论只在高速（近光速）情况下成立，在低速情况下就必须使用牛顿力学？

不不不，也不是这样的逻辑。

狭义相对论跟牛顿力学并不是互补的关系。牛顿力学只在低速时适用没错，但狭义相对论不仅在高速时适用，在低速时也同样适用。而且，在低速时它的精度比牛顿力学还要高。

也就是说，狭义相对论不管在低速、高速时都成立，牛顿力学只是狭义相对论在低速情况下一个还算不错的近似。既然狭义相对论的适用范围那么广，质能方程的适用范围自然也很广，而不是只局限在核反应里。

但是，爱因斯坦并不需要知道核反应里质量和能量的关系，他直接从狭义相对论的基本原理出发，就无可辩驳地得到了E=mc²。这是最让人震惊的地方，也是理性的巨大胜利。

接下来，我们就来看一看，看看为什么只要坚持狭义相对论的基本原理，只要坚持物理定律在洛伦兹变换下保持数学形式不变（洛伦兹协变性），我们就能得到质能方程E=mc²。

02动量守恒定律

再来看看E=mc²，公式的左边出现了能量E，看到能量我们就会想起能量守恒定律。既然是定律，那我们就要问了：你可不可以在洛伦兹变换下保持数学形式不变啊？如果可以，那就欢迎进入狭义相对论的世界；如果不行，那就从哪来回哪去，一边玩去。

不过，考虑到能量的种类太多太杂，我们先来看看更简单的动量守恒定律。

在牛顿力学里，动量的定义是mv（质量乘以速度），在不受外力或合外力为0时，两物体碰撞时动量守恒。

比如，两个质量都为m的小球以相等的速度v迎面撞上，碰撞后两个小球黏在了一起。如果以某个小球的运动方向为正（假设为向右），那这个小球的动量就是mv，另一个小球的动量就是-mv，碰撞前动量之和就是mv+(-mv)=0。

根据动量守恒定律，碰撞后小球的总动量也应该为0。而碰撞后它们又黏在了一起，变成了一个质量为2m的大球，所以碰撞后的速度就必然为0（不然总动量就不为0了）。

两个质量相等、速度相反的小球迎面相撞，碰撞后两个小球黏在一起并保持静止。这个事情很容易理解，不管是用牛顿力学的动量守恒定律来计算，还是根据常识来判断都没错。

但是，我们关注的并不是碰撞本身，而是：动量守恒定律是定律么？

这个问题好像很奇怪，动量守恒定律当然是定律了，不然这名字是瞎叫的么？

但是，我希望来到这里的读者，对定律要有更深层的理解。前面说了，狭义相对论和牛顿力学的核心区别，就是前者的物理定律在洛伦兹变换下保持数学形式不变，后者的物理定律在伽利略变换下保持数学形式不变。

那么，当你把动量定义为mv，当你在说动量守恒定律的时候，这个定律是在洛伦兹变换下保持数学形式不变呢，还是在伽利略变换下保持数学形式不变？如果是前者，那这条动量守恒定律就是狭义相对论下的定律；如果是后者，它就是牛顿力学下的定律。

当然，我们很清楚，把动量定义为mv是牛顿力学里的做法。所以，这样的动量守恒定律必然是牛顿力学下的定律，它必然能在伽利略变换下保持数学形式不变。

下面我们来简单地验证一下。

03伽利略变换

要验证动量守恒定律是否可以在伽利略变换下保持数学形式不变，我们就要先搞清楚什么是伽利略变换？搞清楚当我们在说一个定律在伽利略变换下保持数学形式不变时，我们到底在说什么？

其实，伽利略变换也好，洛伦兹变换也罢，都是联系两个参考系的东西。变换嘛，就是把一个参考系的物理量变到另一个参考系里去。

比如，我在300km/h的高铁上，觉得前面的椅子速度为0，列车员正以5km/h的速度往车头走，这是高铁系的测量结果。

那么，如果我站在地面，地面系测量椅子和列车员的速度又会是多少呢？有同学立马会说：“我知道，从地面上看，高铁上椅子的速度是300km/h，列车员的速度是300+5=305km/h。"

如果我问他这样算的依据是什么，他会觉得这还要什么依据，这不是天经地义的事情么？当然要有依据，物理学是一门非常严密的科学，做什么都要有理有据。

我们现在讨论的是同一个东西（椅子、列车员）在不同参考系里的速度，这就涉及两个参考系之间的变换，是一件很严肃的事情。如何把这两个参考系里的物理量联系起来？答案就是前面说的伽利略变换、洛伦兹变换。

在牛顿力学里，我们用伽利略变换联系两个惯性系，那伽利略变换到底长啥样呢？

假设我们在地面系S建立了一个坐标系（x,y,z,t），现在有一辆火车以速度v沿x轴正方向匀速运动。我们在火车系S’里也建一个坐标系（x’,y’,z’,t’），为了简化问题，我们让这两个坐标系一开始是重合的。

坐标系建好后，空间中发生了任何事件，地面系和火车系都会记录下这个事件的时空信息（x,y,z记录空间信息，t记录时间信息）。我们想知道的就是：地面系和火车系记录的时空信息之间有什么联系？

不同的变换会给出不同的答案，伽利略变换的答案是：

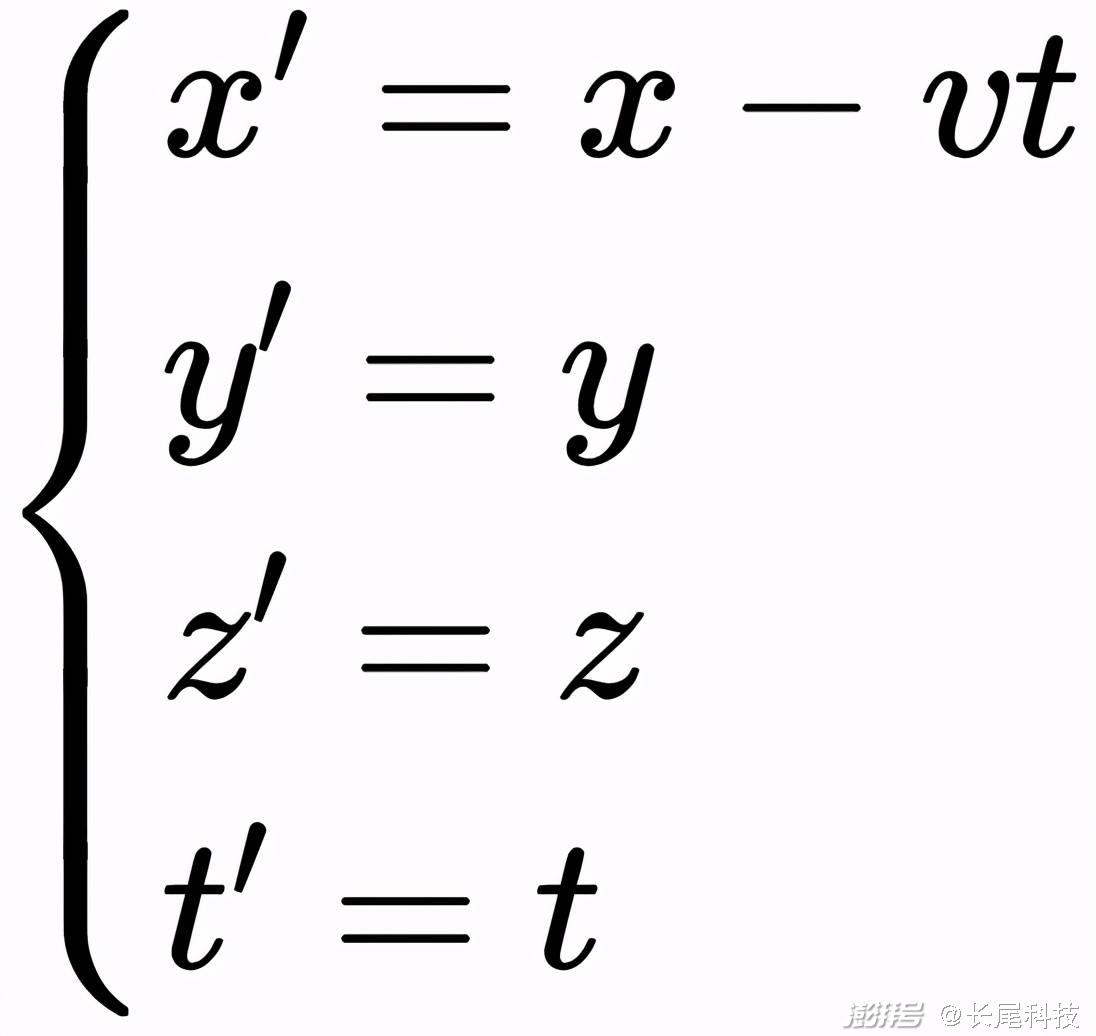
我们知道，牛顿力学里的时间是绝对的，所有参考系的时间都一样，所以伽利略变换里有t'=t。因为t‘代表火车系的时间，t代表地面系的时间，t'=t不就是说大家的时间都相等，时间是绝对的么？

再看空间，因为火车只沿x轴正方向移动，所以火车系和地面系在y轴和z轴的坐标都一样，x坐标的关系x'=x-vt也不难理解，琢磨一下就明白了。

有了坐标和时间的关系，我们很容易就能求出火车系的速度u'和地面系的速度u之间的关系：u‘=u-v。这个就不推了，不清楚的可以看看《相对论前夜：牛顿和麦克斯韦的战争》，里面有更加详细的推导。

伽利略变换的速度关系是u‘=u-v，这就意味着：火车系测量的速度等于地面系测量的速度减去火车相对地面的速度。

比如，在速度v=300km/h的高铁上，如果高铁系测量列车员的速度u'=5km/h，地面系测量列车员的速度u就应该满足：5=u-300，u确实等于5+300=305km/h，跟我们的直觉一样。

但是，我们要清楚地认识到：这些推理都是建立在伽利略变换的基础上的。

因为我们采用了伽利略变换，所以两个惯性系之间的速度才可以这样叠加。火车系测量的速度是5km/h，地面系的结果是300+5=305km/h，这不是什么天经地义的事情，而是伽利略变换的结果。

04牛顿力学的定律

有了这个认识，我们再思考一下：当我们说动量守恒定律是牛顿力学里的定律时，我们到底在说什么？

在牛顿力学里，动量的定义是质量乘以速度，也就是mv。我想看动量守恒定律是不是定律，就是要看在一个惯性系（比如火车系）里成立的动量守恒定律，用伽利略变换把它变到另一个参考系以后，它是否依然成立。

因为质量是一个不变量，不管在哪里都不变。所以，不同惯性系之间动量的差别就体现在速度v上了。

还是以小球的碰撞为例，假设两个质量都为m的小球以速度v迎面相撞，碰撞后两个小球黏在一起并保持静止。取向右的方向为正，从地面系看，碰撞前两个小球的动量分别为mv和-mv，碰撞前总动量为0。碰撞后，两个小球黏在一起并保持静止，所以碰撞后的动量2m×0=0，也是0。

因为碰撞前的总动量等于碰撞后的总动量（都是0），所以，地面系确实认为存在动量守恒定律。

但是，我们看动量守恒定律是不是牛顿力学下的定律，并不是只看这个定律在地面系是否成立，还要看用伽利略变换把它变到另一个惯性系之后，它是否依然成立。

因此，我们要换一个参考系，看看新参考系里的碰撞过程是否依然满足动量守恒定律。为了计算方便，我们就把新参考系选在从左往右运动的小球身上，也就是站在速度为v的小球上再来看这个问题。

在地面系，两个小球碰撞前的速度分别为v和-v，碰撞后两个小球黏在一起，速度为0。那么，在新参考系里，碰撞前后小球的速度又分别是多少呢？

在牛顿力学里，我们使用伽利略变换的速度叠加公式u‘=u-v联系两个惯性系之间的速度。也就是说，在原参考系里速度为u的物体，在新参考系里速度就是u‘=u-v。

因此，对于碰撞前速度为v的小球，在新参考里速度为v-v=0；碰撞前速度为-v的小球，在新参考系里速度为-v-v=-2v；碰撞后速度为0的小球，在新参考系里的速度为0-v=-v。

也就是说，同样的碰撞，新参考系看到的是：两个质量为m的小球，一个速度为0（以它为参考系，速度当然为0），一个速度为-2v（对面的小球），它们碰撞之后黏在一起，变成了质量为2m，速度为-v的大球。

那么，在新参考系里动量守恒定律还成立么？我们再来验算一下：碰撞前两个小球的动量分别为m×0=0和m×（-2v）=-2mv，碰撞后黏在一起的大球的动量为2m×（-v）=-2mv。

看到没有，新参考系里碰撞前后的动量都是-2mv，依然相等。所以，在新参考系里动量守恒定律依然成立。

当然，这里我们只验证了一个新参考系。但是，你完全可以根据伽利略变换的速度叠加公式，证明只要把动量定义为mv，动量守恒定律在一般情况下都成立。

这样，我们才敢理直气壮地说：如果把动量定义为mv，动量守恒定律的确是牛顿力学里的定律。因为你用伽利略变换把动量守恒定律变到任何惯性系，它都成立。

那么，到了狭义相对论里呢？

05洛伦兹变换

在狭义相对论里，联系两个惯性系的不再是伽利略变换，而是全新的洛伦兹变换：

变换的细节我们先不细究，不过你可以看到：在洛伦兹变换里，火车系的时间t'和地面系的时间t不再一样（t'≠t），它们之间有个巨复杂的关系。

也就是说，在狭义相对论里，时间不再是绝对的，不同惯性系的时间并不一样，每个惯性系都有自己的时间。

再看看火车系和地面系的x坐标之间的关系，也是一个非常复杂的式子。所以，不难想象，从洛伦兹变换推出的速度叠加公式肯定就没有伽利略变换的那么简单。

中间的推导过程我就省了，洛伦兹变换下的速度叠加公式是这样的：

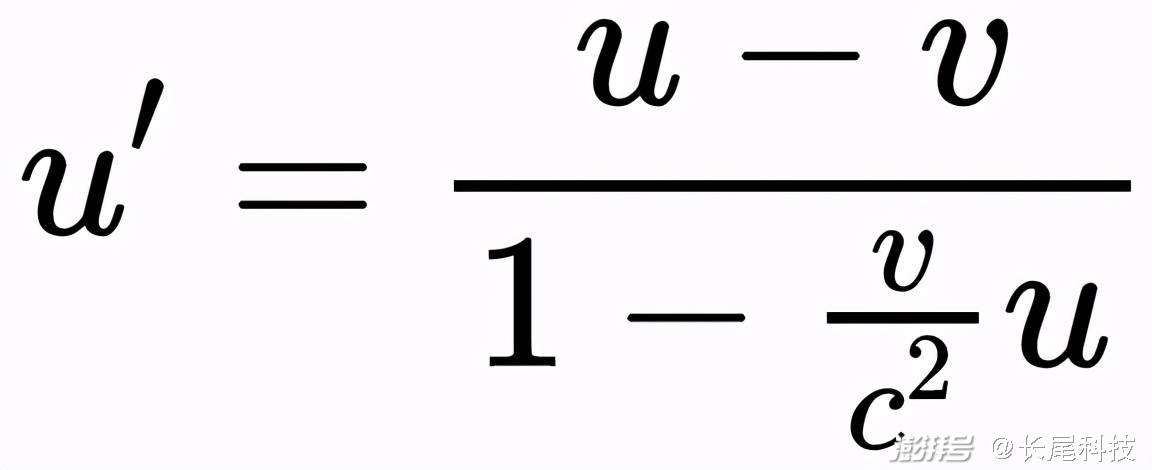
怎么样，比伽利略变换下的u'=u-v复杂多了吧？

但是，仔细观察一下就会发现，如果v远小于光速c，分母的v/c²就约等于0，分母就变成了1，于是这个速度叠加公式就回到了伽利略变换下的u'=u-v。因为牛顿力学是狭义相对论的低速近似，所以伽利略变换自然也是洛伦兹变换的低速近似。

在牛顿力学里，我们使用伽利略变换导出的速度叠加公式，所以可以用300+5=305km/h表示地面系测量的列车员速度。但是，我们在狭义相对论里使用的是洛伦兹变换导出的新速度叠加公式，那结果肯定就不再是305km/h了。

也就是说，如果火车系测量列车员的速度为5km/h，我问地面系的结果是多少？牛顿力学给出的结果是305km/h，这是用伽利略变换算出来的；狭义相对论认为这个结果不等于305km/h（当然也极为接近这个数字），因为它是用洛伦兹变换算出来的。

如果你问谁算得更准确，那当然是狭义相对论的结果更准确，但牛顿力学的结果也跟它极为接近。因为火车的速度v和列车员的速度u都太小了（相对光速c），所以洛伦兹变换的速度叠加公式的分母1-vu/c²基本上等于1，于是基本上就等于伽利略变换的结果。

但是，如果火车的速度接近光速，分母1-vu/c²就会远小于1，那得到的结果就跟伽利略变换完全不一样了，所以牛顿力学就不能用了。

通过这个例子，相信大家对伽利略变换和洛伦兹变换都有了一定的了解，也明白不同变换下的速度叠加公式是不一样的。具体的计算过程可以不用搞得太清楚（亲自推一遍当然更好），但道理一定要明白。

06狭义相对论的定律

知道了洛伦兹变换，我们再来看这个问题：在狭义相对论里，动量守恒定律还是定律吗？

当我们在说这句话的时候，我们的意思是：如果把动量仍然定义为mv，那动量守恒定律在洛伦兹变换下还能保持数学形式不变么？如果动量守恒定律在一个惯性系里成立，我用洛伦兹变换把它变到另一个惯性系以后，它还成立吗？

具体的计算我就不做了，稍微想一下就知道答案肯定是否定的。

因为我们已经证明了：如果把动量定义为mv，动量守恒定律在伽利略变换下是可以保持数学形式不变的，这样动量守恒定律才步入了牛顿力学的殿堂。

然而，现在动量的定义（mv）没变，联系两个惯性系之间的变换却从伽利略变换变成了洛伦兹变换。既然伽利略变换能让动量守恒定律保持数学形式不变，那换了变换以后肯定就不一样了啊。

也就是说，如果我们依然把动量定义为mv，在洛伦兹变换下，新参考系的动量守恒定律必然不再成立。

要验算也很简单，洛伦兹变换下的速度叠加公式是这样的：

还是刚才的小球碰撞问题，我们可以用同样的方法把新旧惯性系碰撞前后的速度都算出来，再看看动量是否相等。

谁算谁知道，答案必然不相等。

于是，我们就面临一个非常棘手的问题：如果我们在狭义相对论里依然把动量定义为mv，那么，经过洛伦兹变换以后，新参考系里的动量守恒定律就不再成立。如果动量守恒定律无法在洛伦兹变换下保持数学形式不变，那它就没有资格成为狭义相对论里的定律。

也就是说，如果我们继续沿用牛顿力学的动量定义（mv），那狭义相对论里动量守恒定律就不再成立。

怎么办？

解决方案也很明显：要么，我们放弃动量守恒定律，认为狭义相对论里动量守恒定律不再成立；要么，我们修改一下动量的定义，让新定义下的动量守恒定律在洛伦兹变换下依然可以保持数学形式不变，从而保住它在狭义相对论里的定律地位。

很显然，闭着眼睛我们都知道要选后者。

动量守恒定律这么重要的东西，你说放弃就放弃了？为了坚持动量的定义（mv）而放弃动量守恒定律，这种行为太愚蠢了。如果动量守恒定律不再成立，我要动量有何用？

07新的动量

所以，为了保住狭义相对论里的动量守恒定律，我们需要重新定义动量。重新定义的目的，就是让新的动量守恒定律具有洛伦兹协变性，让它在狭义相对论里能继续以定律自居。

那么，我们要把新动量定义成啥样，才能让它具有洛伦兹协变性呢？这个倒不难，因为洛伦兹变换是明确给出了的，我们只要凑出一个新动量，让动量守恒定律在洛伦兹变换下依然可以保持数学形式不变，而且在速度远小于光速时能够回到牛顿力学的定义就行了。

这个过程我略了，感兴趣的自己去试一下。最后，为了保住狭义相对论里的动量守恒定律，我们必须把动量定义成这样：

可以看到，当v远小于光速c时，分母就会变成1，此时的动量就回到了牛顿力学的定义mv。而且，你试一试，这样定义动量，确实可以让动量守恒定律在洛伦兹变换下保持数学形式不变，皆大欢喜。

到这里，我们就完成了从牛顿力学到相对论力学升级的第一步。为了让动量守恒定律具有洛伦兹协变性，我们修改了动量的定义。

但是，力学量又不止动量一个，物理定律也不止动量守恒定律一个。你考虑了动量守恒定律，那能量守恒定律要不要考虑？你改了动量的定义，那动能的定义要不要改？

改，当然要改，一个个排队慢慢来！

为了让动能不跟新的动量发生矛盾，为了让能量守恒定律也能顺利入驻狭义相对论，我们需要同步修改动能的定义。

而接下来，就是见证奇迹的时刻：一旦开始修改动能的定义，你会发现质能方程E=mc²竟然神奇地冒出来了。

08新的动能

狭义相对论里的动能要怎么改呢？当然是照着牛顿力学慢慢改。

在牛顿力学里，动能的定义是mv²/2。一个质量为m的木块静止在地面，它的动能为0，我用一个恒力F推这个木块，木块移动了距离S，速度均匀加速到了v。

我在《什么是高中物理？》的第25节跟大家算过：一个物体在恒力F的作用下会以一定的加速度做匀加速运动。根据牛顿第二定律，这个力F和物体的质量m以及加速度a之间的关系是：F=ma。而一个物体以加速度a从0加速到v，运动的距离S可以表示成：S=v²/2a。

如果我们算一下力F在空间上的累积（也就是力F做的功）F·S，会发现它刚好就等于物体增加的动能mv²/2：

也就是说，合外力对物体做的功等于动能的改变量，这就是中学的动能定理。也因如此，我们在牛顿力学里可以用合外力F和位移S的乘积F·S来表示动能增加的大小，如果物体一开始动能为0，那F·S就是物体最终的动能。

那么，牛顿力学里这个关于动能的计算方式可不可以搬到狭义相对论里来呢？

大抵还是可以的，毕竟狭义相对论在低速情况下还要回到牛顿力学，所以许多东西都会保持一定的一致性。比如，狭义相对论里的动量虽然不再是mv，但是基本形式上还是质量m乘以速度v，只不过加了一个相对论特有的系数。

因此，我们在狭义相对论里就暂时用F·S计算动能好了。位移S好说，但问题是：这个力F要如何表示？

在牛顿力学里，力F的常见表示有两种：一种是根据牛顿第二定律F=ma来算；另一种是对F=ma做一个微小的变形，把加速度a按照定义表示成Δv/Δt，然后把m和Δv组合成动量的改变量Δp（p=mv），然后F=ma=mΔv/Δt=Δp/Δt。

也就是说，对于力F，我们既可以把它表示成质量m和加速度a的乘积，也可以把它表示成单位时间内动量的变化量，也就是动量的变化率Δp/Δt。然而，狭义相对论里的新动量我们已经找到了，那就直接用动量的变化率Δp/Δt表示F，再用F·S计算物体的动能吧，省时省力。

然后，我们要意识到一件事：前面我们都假设力F是恒力，认为物体在做匀加速运动，这是一种特例。

我们要计算物体的动能，要推导质能方程，当然不希望它只在这种特殊情况下才成立。所以，我们要考虑更一般的情况：如果力F和位移S都在变，我们应该如何计算它们的乘积？

地球的表面是弯的，但在小范围内我们可以认为它是平的。同理，在足够小的范围内，我一样可以认为力F和位移S的大小不变。如果用ds表示这个微小的位移变化，用F·ds表示力F在这个微小位移里做的功，那么，把0到S所有的功累加起来就能得到总动能E。

写成数学表达式就是这样：

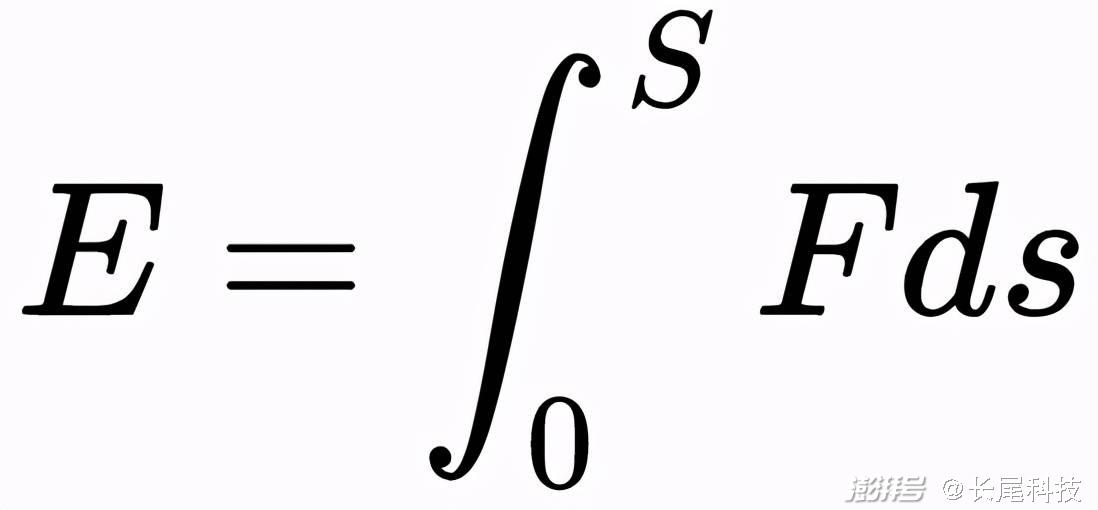
很显然，为了保证结果的一般性，我们这里动用了微积分。这个具体的计算过程我不想多讲，因为但凡学了微积分，会分部积分的同学都知道怎么算。如果你不会微积分，这个计算过程我也没法在这里给你科普，我只能建议你先看看我的《你也能懂的微积分》，再找本微积分教材看看。

更为重要的是：这个计算过程并不会影响你对质能方程的理解。

因为这只是一个纯数学计算手段。人们之所以误解质能方程，并不是因为不知道这个公式的形式是E=mc²，而是无法理解这个方程背后的物理意义和物理背景。

如果你跟着我的思路来到这里，知道为了让动量守恒定律满足洛伦兹协变性，我们不得不重新定义了动量，进而需要重新定义动能。你就会知道质能方程到底是怎么来的，就算看不懂中间的计算过程，也不会影响你对质能方程的理解。

这里，我就放一张新动能的推导图片，你能看懂就看，看不懂也没事。当然，如果你暂时看不懂，但是为了能看懂而去学习微积分，那自然是极好的。这里也没多少微积分的知识，关键就是一个分部积分。计算思路也非常简单，就是用狭义相对论里新动量的变化率代替力F：

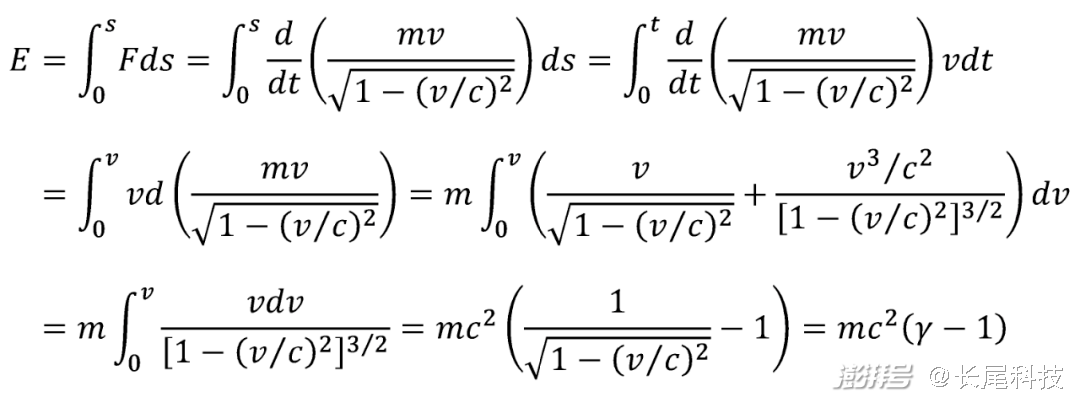
我把结果放到倒数第二步：

也就是说，一个物体的动能E在狭义相对论里可以表示成这样：括号外面是mc²，括号里面是相对论因子减去1。

我们把中间那一大串东西称为相对论因子（也叫洛伦兹因子），因为相对论里经常会用到它，所以我们就用一个特殊符号γ来表示这个相对论因子：

这样，你再看看狭义相对论里的新动量，是不是就相当于在牛顿力学的动量mv上乘了一个相对论因子γ？也就是说，狭义相对论里的新动量可以简写成p=γmv。

同样，上面的动能表达式一样可以通过相对论因子γ简写为：

在这个式子里，m依然是我们熟知的质量，是一个不随速度和参考系变化而变化的物理量。而这个E，就是因为有力F作用在物体身上，物体因为运动而具有的动能。

这个动能的形式很有意思。

在牛顿力学里，动能的表达式是mv²/2，只有一项；到了狭义相对论，动能的表达式竟然有两项。而且，后一项mc²竟然跟物体的速度v没有关系，只跟物体的质量m有关，只有前一项γmc²才会随着速度的增大而增大（因为γ会随着速度的变大而变大）。

这有点拔出萝卜带出泥的味道，原本我们只是在正正经经地计算狭义相对论的新动能。现在你倒好，你算出的新动能里竟然还有一项跟速度无关的mc²，单位还跟能量一样。

仔细看看这个新动能，如果物体的速度v为0，相对论因子γ就等于1，那动能就变成了E=mc²-mc²=0。静止物体的动能为0，很符合我们对动能的认知。

如果物体的速度开始增大，相对论因子γ就开始大于1，第一项γmc²就在增大，它跟mc²的差值也会不断增大，结果就是动能不断增大。

这给人的感觉，就好像是物体静止时具有mc²的能量，当物体开始运动时，我们用γmc²减去物体静止时具有的能量mc²就得到了物体的动能。所以，爱因斯坦面对这个式子时，创造性地把mc²解释为质量为m的物体静止时具有的能量，简称静能。

如果我们把mc²解释为物体的静能，而E是物体的动能，那静能+动能自然就是物体具有的总能量。于是，γmc²就成了物体具有的总能量（动能+静能）。

这样解释的话，是不是一切都合情合理了呢？

09质能方程

复盘整个过程，我们到底做了什么？

我们只是坚持狭义相对论的基本原理，认为物理定律在洛伦兹变换下应该保持数学形式不变，也就是认为物理定律应该具有洛伦兹协变性。

然后，为了让动量守恒定律具有洛伦兹协变性，我们修改了动量的定义。动量修改了以后，动能自然也得跟着改。然而，令谁也没有想到的是：当我们把这种符合狭义相对论精神的新动能（E=γmc²-mc²）计算出来以后，发现它竟然带了一个尾巴mc²。

接着，爱因斯坦认为mc²应该是物体静止时具有的能量，也就是静能，γmc²是物体的静能和动能之和，也就是物体的总能量。

整个过程，我们唯一引入的就是狭义相对论的基本原理，也就是认为物理定律应该具有洛伦兹协变性，然后就发现狭义相对论的新动能把静能mc²带出来了，这太意外了！

于是，我们就从狭义相对论里自然而然地推出了质能方程：E=mc²。

不知道爱因斯坦看到这个结论后是什么反应，这只是牛顿力学向相对论力学升级过程中的一个小步骤，结果却发现能量和质量之间竟然有E=mc²这样一种神奇的关系。

这个结论看起来是如此的不可思议，因为真空光速c是一个非常大的数字（3×10^8m/s），平方一下就更大了。根据质能方程，一个半斤重的苹果蕴含的能量将高达525万吨TNT当量，大致相当于350颗广岛原子弹爆炸释放的能量，这太夸张了。

但是，E=mc²又是直接从狭义相对论的基本原理直接推出来的，如果质能方程错了，那就是狭义相对论错了。而爱因斯坦对狭义相对论的信心是极强的，所以，他在写完《论动体的电动力学》的三个月后，就完成了质能方程的论文。

10回到牛顿

习惯了将动能视为mv²/2的人可能不太习惯E=γmc²-mc²这种新动能表达式。但是，因为牛顿力学是狭义相对论的低速近似，所以它在低速条件下依然可以回到大家熟悉的mv²/2，不信我们来试一试。

把相对论因子γ进行泰勒展开，就得到了这样的结果：

泰勒展开就是看你想近似到什么程度，你不是说牛顿力学是相对论力学的低速近似么？那相对论力学要低速近似到什么程度才会变成牛顿力学呢？泰勒展开会告诉我们答案。

如上图，我们对一张真实照片进行了“泰勒展开”。一阶近似下就是随便描了一个轮廓，我们可能看了个寂寞；二阶近似下可以看清楚一些细节，图片变清楚了一些；三阶近似下，细节就更清楚了，更接近原图……

只要你开心，你可以无限阶近似下去，近似的阶数越高，图片就越接近原始图片。同理，我们对相对论因子γ进行泰勒展开，它就被分成了无穷多项的叠加，你可以按照自己的需求采取相应的近似水平。

我们说牛顿力学是相对论力学的低速近似，这个低速是相对于光速而言的。当速度v远小于光速c时，v/c就是一项很小的项，（v/c)²以及更高次项就是更小的项了，可以选择性忽略。

那么，如果我们只取前两项，也就是取γ=1+（v/c)²/2，再把γ代入狭义相对论的新动能：E=γmc²-mc²=mc²（γ-1）=mv²/2。不多不少，刚好就回到了牛顿力学的mv²/2。

也就是说，牛顿力学的动能只是狭义相对论动能的一个二阶近似。

因为mv²/2只是一个近似值，所以它必然会丢失一些信息。只是，万万没想到，它丢失的信息里居然包含了物体静止时具有的能量mc²。一旦我们通过更加精确的狭义相对论把这个丢失的信息找了回来，就会发现任何质量为m的物体都含有mc²如此巨大的能量。

其实，静止的物体具有能量一点也不奇怪。

一堆火药放在那里，你肯定知道它有能量，甚至能算出这堆火药爆炸时会释放出多少能量。与此同时，你也知道火药爆炸释放的只是部分化学能，并不是它的全部能量。现在，我们第一次有办法把它的全部能量算出来了，途径就是质能方程E=mc²。

质能方程把质量和能量联系起来了。那么，在这种新视角下，我们应该如何看待质量和能量的关系呢？

11质量与能量

再次回到狭义相对论的动能表达式：

回想一下，爱因斯坦是如何解释这个式子的？爱因斯坦想：既然E是物体的动能，那么γmc²就是物体的总能量，mc²是物体静止时具有的能量，简称静能。

注意，我们是先得到了动能E，是先有能量，先有总能量γmc²和静能mc²，然后再考虑如何衡量能量的大小。因为c是常数，所以就只能用质量m来衡量静能的大小，这个次序不能乱。

于是乎，质量就成了能量的量度。

因此，如果物体吸收了一点能量，它静止时的能量增加了，质量也会增加；如果物体释放了一点能量，它静止时的能量减少了，质量也会减小。

所以，把质能方程写成m=E/c²反而更容易理解它的含义（爱因斯坦一开始就是这么写的）：你想知道一个物体的质量是多少吗？那就用它静止时的能量除以c²吧，于是我们才说质量是能量的量度。

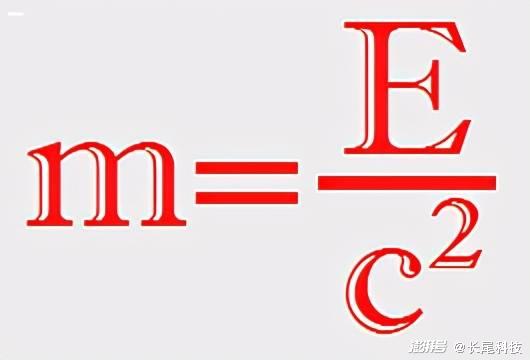
一个物体静止时的能量是多种多样的，可以有内能、化学能、核能以及各种势能。但是我不关心种类，你把它们都加起来，除以c²就能得到物体的质量m。

为什么我要如此小心翼翼地描述这一段呢？因为只有极少数人在看到质能方程E=mc²后会认为它是在说“质量是能量的量度”，许多人的第一反应是：质能方程意味着“质量可以转化成能量”。核反应里出现了质量亏损，就是一块“实实在在”的物质丢失了一块质量，然后它们转化成了“虚无缥缈”的能量。

这是一种非常常见，但危害极大的误解。顺着这种误解，稍微发散一下就能搞出太极相对论、佛学相对论之类的东西。你以为原子弹释放了能量，是因为原子弹爆炸时丢失了一块东西，然后这部分质量转化成了能量？

不不不，原子弹爆炸释放能量的过程，跟一般的火药爆炸没什么不同，只不过前者释放的能量比较多，后者释放的能量比较少而已。原子弹爆炸释放了能量，所以度量原子弹能量的质量会减少；火药爆炸释放了能量，所以度量火药能量的质量也会减少。

这就是一个普通的能量转化过程，体系的一部分能量（原子弹的核能，火药的化学能等）通过爆炸转化成了动能和其它能量。于是，原子弹和火药的能量E减少了，度量这个能量的质量m也相应减少了，并且遵守E=mc²，仅此而已。

这也是我比较讨厌“质量亏损”这个词的原因，它太容易让人误解了，太容易让人误以为质量只在核反应中才会减少，让人误以为核反应就是“质量转化成了能量”。

没有什么质量转化成了能量，只有质量是能量的量度，质量就是度量一个物体静止时具有多少能量的。

我知道，不管我在这里说什么，你都难以接受为什么我们不能说“质量转化成了能量”，你不认为这样有什么不妥，甚至觉得它理所当然。而且，就算我让你强行记住这个结论，你后面还是会忘的，毕竟大家都习惯用自己习惯的方式思考。

所以，我们就来深入地扒一扒，看看你在说“质量转化成能量”时，你到底在说什么？看看为什么很多人会这样想，以及最重要的：为什么质能方程E=mc²不能这么理解？

12牛顿的质量

在牛顿时代，大家认为宇宙万物都是由微小的实物粒子（原子）组成，认为宇宙就是一堆粒子的集合，各种物理现象只是粒子间的排列组合和运动变化，而粒子的运动规律则由牛顿力学给出。

在这样的语境下，人们认为组成物质的基本微粒是不可摧毁的，自然界的各种变化只是它们的排列组合，并不会摧毁粒子本身。到了18世纪，化学家们在一定精度内发现化学反应前后物质的总质量不变，也就是大名鼎鼎的质量守恒定律，这就更加佐证了这种观点。

因为化学反应只是原子间的排列组合，如果原子的种类和数目都没变，那原子的总质量就不变，质量自然就守恒了。

一旦我们认为“一个物体的质量等于组成这个物体的所有微粒质量之和”，质量基本上就被当成了物质的代名词。因为，你潜意识里会觉得：只要是物质，肯定就由一些实物微粒组成，它的质量自然就等于所有微粒的质量之和。

那能量呢，能量在这种语境下又扮演了什么角色？

还是看化学反应，我们认为化学反应就是原子间的排列组合。比如木炭燃烧，在化学家眼里就是木炭里的碳原子和空气中的氧原子重新组成了二氧化碳分子，这个过程释放了能量，但燃烧前后原子的种类和数量都没变，所以质量不变。

也就是说，化学家认为虽然木炭燃烧释放了能量，但它们的质量不会变。在这种语境下，质量和能量明显是不同的东西：质量是组成物质的所有原子质量之和，能量不过是原子在重组过程中释放出来的副产品。

正因为牛顿语境下的质量和能量是如此的不同，我们在第一次看到质能方程E=mc²，第一次听说在核反应里会发生违反质量守恒定律的“质量亏损”时，才会认为这是“质量转化成了能量”，是组成物质的实物粒子实实在在地被摧毁了（质量减小），然后神奇地转化成了能量。

但问题是，质能方程E=mc²并不是牛顿力学的东西，而是狭义相对论的天之骄子啊。

相对论和量子力学是20世纪物理学的两大革命，它们颠覆了牛顿力学的许多观念。物质不能再简单地看作一堆实物粒子的集合，质量不再是组成物体粒子的质量之和，化学家发现的质量守恒定律也不再成立……

总之就是，时代变了，世界变了，一切都变了，原来的“质量转化成能量”自然也得跟着变。所以，如果我们想搞清楚为什么不能再那样思考，就得先搞清楚牛顿的观念是如何被打破的？

13电磁场的挑战

狭义相对论是爱因斯坦在协调电磁理论和牛顿力学的过程中建立起来的，所以它的论文就叫《论动体的电动力学》（公众号后台回复“狭义相对论论文”获取原论文）。

我们也知道，在19世纪建立电磁大厦的过程中，有两个人的作用至关重要，他们是法拉第和麦克斯韦。

法拉第创造性地提出了“场”，用电磁场来描述电磁现象。麦克斯韦则用优美的数学语言把法拉第的思想表现了出来，得到了能够描述一切经典电磁现象的麦克斯韦方程组。

这些历史大家都很熟悉，但是很多人没有注意到：法拉第提出的电磁场，其实是一个超出牛顿物理图景的概念。

什么意思？在牛顿的观念里，物质是由基本微粒组成的，那电磁场是由什么微粒组成的呢？很显然，电磁场并不由什么微粒组成，这看起来就跟牛顿的物质观发生了冲突。

于是，有些人就主张电磁场只是描述物质的一种数学手段，不具有物理上的意义，也就是不认为电磁场是真实的物质，这样牛顿的物质观就不用对它负责了。但是，很快人们就发现不能这么干，因为电磁场具有能量。

为什么电磁场具有能量呢？

举个例子，我从北京向武汉发射一束电磁波，因为电磁波的速度有限（光速），它从北京到武汉需要一段时间。那么，当电磁波离开了北京，却又还没到武汉时，能量去哪了？此时的能量既不在北京，也不在武汉，那就只能在电磁场里。

于是乎，电磁场就理所当然具有了能量。一个东西具有能量，那它肯定就有物理上的意义，也就是说它是真实存在的物质。如果电磁场是物质，而它又不由实物微粒构成，那就真的跟牛顿的观念冲突了。

但人们还不死心，虽然电磁场是真实存在的物质，但我们还是可以把电磁场和电磁波看作某种实物粒子衍生出来的现象，这样它们的基础就还是牛顿的实物粒子。

比如水波，虽然它是真实存在的，但水波其实是许多水分子有规律的运动衍生出来的现象，它的基础还是水分子这种“微粒”。那么，如果我们认为电磁波跟水波一样，也是由于某种微粒的振动引起的，这不就符合牛顿的观念了么？

按理说，这种想法是非常自然的，毕竟水波、电磁波都是波。但问题是，当我们说水波是由水分子的振动引起时，我们的确看见了水，所以说“水是水波的介质”没什么问题。

但如果你说电磁波也是由某种介质的振动引起的，那这种介质是什么？光就一种电磁波，光可以在太空、真空中传播，而这里似乎什么都没有，不存在什么介质。你总不能说电磁波是由某种介质的振动引起的，但又说不出这种介质是什么吧？

是，电磁波的确有可能存在介质，只是我们还没发现，没发现并不代表它不存在。但是，你也要明白这么做的巨大风险：这是在假设一种看不见、摸不着，目前任何实验都观测不到，却又在太空、真空中广泛存在的介质。

虽然一听就不怎么靠谱，但想到只有这样才能不违背牛顿的观念，人们（包括麦克斯韦、赫兹）就纷纷接受了，并将这种介质命名为以太。也就是说，如果我们把电磁波看作以太的振动，就像把水波看作水的振动那样，它就可以与牛顿的观念和平共处了。

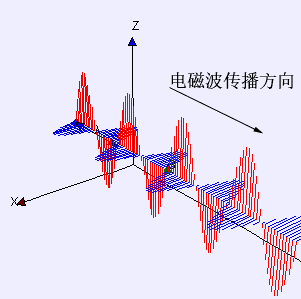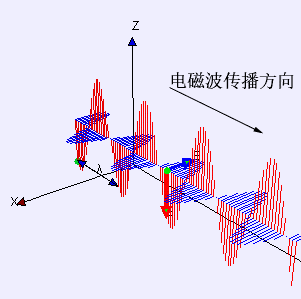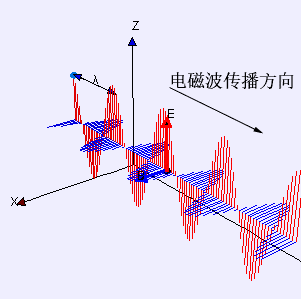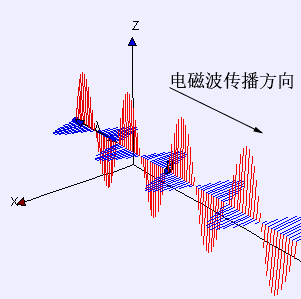
然而，我们都知道爱因斯坦在狭义相对论里把以太仍了，也就是把作为电磁波介质的以太仍了。他认为并不能把电磁波看作以太的振动，电磁波不需要介质，它跟水波有本质的区别。

那有人就要问了：如果电磁波没有介质，它是怎么传播出去的呢？

我反倒想问一句：你凭什么觉得只要是波，就一定要有介质呢？你觉得水波、声波都是通过介质传出去的，所以电磁波也要有介质？

没道理啊，没理由说张三李四是这样，就要求王五也这样。更重要的是，你认为波都有介质，其实就是认为所有的波都跟水波一样，都是通过相邻介质点的力学作用传出去的。但我们已经说了电磁波跟水波不一样，那就不能套这个逻辑了，更多细节可以看看我的《相对论诞生：爱因斯坦是如何创立狭义相对论的？| 主线》。

因此，到了狭义相对论，我们是彻底无法再把电磁波当作某种介质（以太）的振动了，无法再把它还原为某种微粒的衍生现象了，这就跟牛顿的物理图景彻底冲突了。

于是，我们现在就有两种东西：一种是实物微粒，比如分子、原子、质子、中子等，它们看上去可以由更基本的微粒组成；另一种就是无法看成实物微粒的电磁场。

如何把它们统一起来呢？

很显然，牛顿力学是办不到的，我们需要狭义相对论和量子力学才能统一它们。这种包含了狭义相对论、量子力学以及场论思想的全新理论，就叫量子场论。这是一种全新的物理图景，大家熟悉的粒子物理标准模型就是在这上面建立起来的。

怎么统一实物粒子和场呢？无非就是两种思路：要么认为粒子更基本，场是粒子的某种衍生物（牛顿物理干不了这事，现代物理学里倒是有人这么考虑，比如温伯格）；要么就认为场更基本，粒子是场的某种衍生物。

量子场论的主流思想是后一种，也就是认为场更加基本，粒子只是场的激发态。比如，电磁场是更基本的，电磁场的激发态就是光子；质子场是更基本的，质子场的激发态就是质子，以此类推。

量子场论认为万物皆场，场是更加基本的东西。粒子只是这种量子化场的激发态，场与场之间的相互作用决定了要发生的一切。具体细节这里就不多说了，后面科普量子力学时再细说。

总之，到这里大家就应该清楚了：牛顿的物理图景已经崩塌了，物质并不是由坚不可摧的实物粒子组成的。在更现代的量子场论里，场反而是更加基本的东西，粒子只是场的激发态。

如果你记住了这一点，质能方程E=mc²就非常容易理解了。因为质能方程最难以理解的地方，就是你非要用牛顿的观念，来理解这个已经完全超出了牛顿物理学的东西。

量子场论是狭义相对论和量子力学联姻的产物，因此必然能跟质能方程相容。我这里并不要求你理解量子场论，只要你能意识到不能再用牛顿的观念来思考质能方程，后面的一切就都好说了

打了这样的预防针，我们再来看看经常跟质能方程同时出现的质量亏损。

14质量亏损

进入20世纪，人们发现了一件“奇怪”的事情：组成原子核的核子质量之和，竟然比原子核本身的质量要大。

什么意思？我们知道原子核是由质子和中子组成的，比如氘核就是由一个质子和一个中子组成。按照原来的观念，我们肯定认为氘核的质量等于一个质子的质量加上一个中子的质量。但实验结果却是：一个质子和一个中子的质量之和比氘核的质量要大。

为什么？

我们对这个结果表示惊奇，是因为它跟牛顿的观念不一样。我们认为一个物体的质量应该等于所有组成物体的微粒质量之和，认为一个氘核的质量应该等于一个质子加上一个中子的质量。但结果却是一个质子（1.6726×10^-27kg）和一个中子（1.6749×10^-27kg）的质量之和（3.3475×10^-27kg）比一个氘核（3.3436×10^-27kg）的质量要大。

而且，我们还知道：质子和中子结合成氘核释放的能量E，跟减少的质量m之间刚好满足E=mc²。

于是，很多地方就用质量亏损来解释这个事，说质子和中子组合成氘核时发生了质量亏损，亏损的质量就按质能方程释放能量。

从牛顿的观念来看，这样考虑是非常自然的。因为质量减小了，肯定就意味着损失了一部分组成物质的“真材实料”，而它刚好又按照质能方程释放了一定的能量，这可不就是损失的质量转化成了能量么？

但问题是，质能方程是狭义相对论的产物，我们不能再用牛顿的观念去思考，因而不能说是“质量转化成了能量”。

那问题到底出在哪？我们应该如何看待质子和中子结合成氘核这个现象？如果不是核原料损失了一部分质量并转化成了能量，那又是什么呢？

问题的关键就在于：单独的质子是质子，跟中子一起组成氘核的质子还是质子，它们并没有什么不同。既然质子的成分都是一样的（两个上夸克和一个下夸克组成），并没有在跟中子组合成氘核的过程中损失什么，你说它质量亏损到底是亏损了什么？

是原来的质子由三个夸克组成，组成氘核之后的质子就损失了一个夸克，只由两个夸克组成了？或者是，你觉得原来的质子是由100个什么微粒组成的，组成氘核的质子就损失了1个微粒，只有99个微粒了？

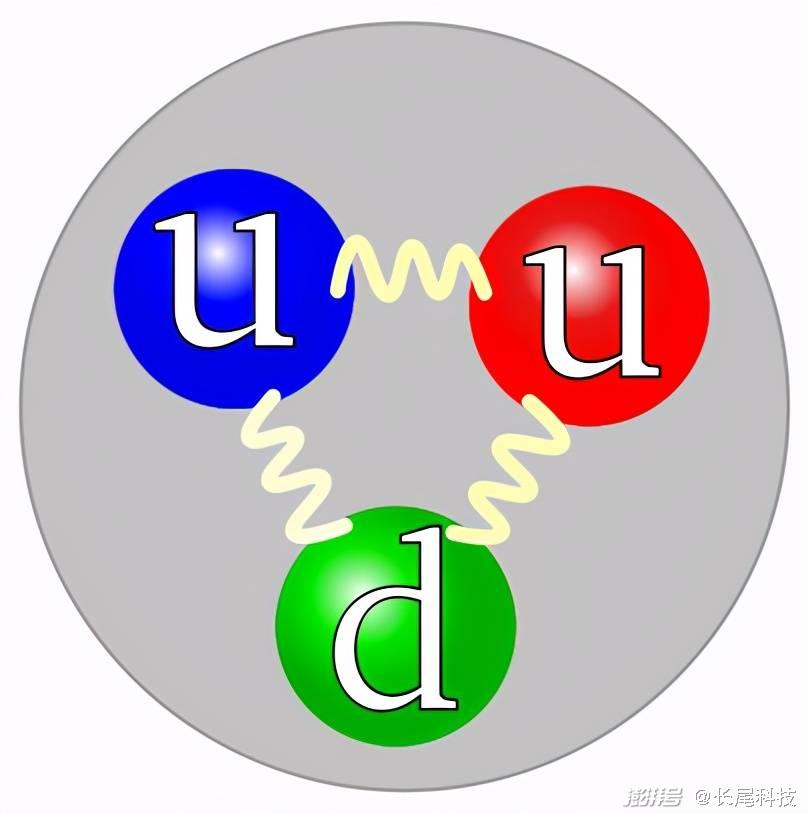
显然，不可能是这样。质子有质子的内部结构，如果它的内部结构发生了变化，那就不是质子了。就像一个质子和一个中子组成了氘核，但如果增加了一个中子，那就不叫氘核，而是氚核。

既然单独的质子叫质子，氘核里的质子也叫质子，那它们就应该是一样的，质子并没有缺胳膊少腿，中子也一样。既然质子和中子都没有损失什么成分，那它们质量亏损到底是亏损了什么呢？它又能亏损什么呢？

出问题了吧？仔细一推敲，你就会发现这个逻辑是行不通的。

但是，在核反应里确实发生了质量亏损啊。质子、中子和氘核的质量都能查到，确实是前两者加起来比后者大，质量确实损失了一部分啊，这到底是怎么回事呢？

大家认为化学反应前后质量守恒，认为两块砖头一起称的质量应该等于单独称的质量之和，为什么质子和中子组成氘核之后质量就减少了呢？难道核反应比较特殊，有它独特的规律？

15核反应特殊吗？

核反应它一点也不特殊！

质子和中子组合成氘核，它是核子（组成原子核的粒子，包括质子、中子以及它们的反粒子）的重新组合，化学反应是原子的重新组合。一个是核子的重组，一个是原子的重组，有什么本质的区别？

核子间的相互作用主要是强力，原子间的相互作用主要是电磁力，除了强力比电磁力要强一些以外，核反应和化学反应没什么太大的不同。

甚至，两块磁铁在磁力作用下吸在了一起，这个过程跟核反应、化学反应也没什么本质的区别，无非就是把核子、原子换成了磁铁，是不是这个道理？

如果核反应没什么特殊，那质子和中子组成氘核释放出能量，碳原子和氧原子组成二氧化碳分子（木炭燃烧）释放出能量，两块磁铁吸在一起释放出能量（没错，的确释放了能量，不然磁铁碰撞时的声音是哪来的？）的过程就应该是类似的。

如果质子和中子组成氘核的核反应会发生质量亏损，那木炭燃烧会不会发生质量亏损？两个磁铁吸在一起会不会发生质量亏损？

有些人可能有点懵，因为他印象里的“质量亏损”是一个非常高级的名词，是一个违背了质量守恒定律的东西。这种反直觉的新玩意，只有全新的相对论与核反应才能与之相配，一般的化学反应怎配享有如此待遇？把两个磁铁放到这里来就更过分了。

而且，中学化学也讲过，化学反应前后物质的总质量是不变的。两个磁铁吸在一起，根据直觉，前后的质量就更加不可能变了。所以，根据直觉和常识，他绝不相信化学反应、磁铁吸在一起也会发生质量亏损。

但是，我上面的推理也很有道理啊，核反应也好，化学反应、磁铁吸在一起也好，都是两个小东西组成了一个大东西，并且都释放了能量。区别无非就是核反应释放的能量大，化学反应释放的能量中等，磁铁吸在一起释放的能量少，并没有什么本质的不同。

还有，质能方程E=mc²是爱因斯坦从狭义相对论的基本原理推出来的，所以，狭义相对论成立的地方质能方程也应该成立。那么，狭义相对论就只在核反应里成立？化学反应和磁铁相吸就不遵守狭义相对论了么？显然不是啊。

因此，从直觉和常识出发，我们觉得只有核反应才会发生质量亏损，亏损的质量和释放的能量满足质能方程。从逻辑和推理出发，又似乎是核反应、化学反应、磁铁吸在一起的过程都会出现质量亏损，亏损的质量跟释放的能量之间都满足质能方程。

直觉和逻辑发生了冲突，我听谁的？

当然是逻辑，科学从来就不是为了符合你的直觉而建立的。你要说直觉，亚里士多德的理论最符合直觉了，牛顿的都很反直觉，更别说相对论了。

所以，我们应该相信核反应、化学反应、磁铁吸在一起的过程中都发生了质量亏损。

如果化学反应也有质量亏损，那亏损的质量m跟化学反应（比如木炭燃烧）释放的能量E之间也会满足E=mc²。只不过，化学反应释放的能量E比较少，而光速c又很大，所以根据E/c²算出来的亏损质量m就非常小，小到平常根本察觉不出来，于是化学家们才总结出了质量守恒定律。

至于磁铁，它们吸在一起时释放的能量就更少了，亏损的质量也就更小。所以，我们就更加不会察觉分开的磁铁与吸在一起的磁铁在质量上会有什么不同了。

这样，我们就能以一种统一的逻辑解释所有的事情，既不与理论相冲突（从狭义相对论推出的E=mc²是普适的，核反应、化学反应、磁铁都应该遵守），也不跟实验相冲突（核反应容易观测到，化学反应、磁铁不太容易观测到）。

那问题的关键就来了：如果这种逻辑是对的，如果核反应、化学反应甚至磁铁吸在一起释放能量时都发生了质量亏损，而我们又不能像牛顿那样认为是组成物质的“材料”少了一块，那它到底亏损了什么？为什么它的质量会减少？

这就涉及到一个非常关键问题：在狭义相对论里，我们应该如何看待质量？

16质量是能量的量度

木炭燃烧时，碳原子和氧原子结合成二氧化碳分子，这个过程释放了能量，相应的质量也亏损了一点。这个结论已经不奇怪了，我们奇怪的是：它的质量为什么会减小？

如果我们还用牛顿的观念思考这个问题，你就会发现怎么也想不通。你觉得一个物体的质量是组成这个物体的所有粒子质量之和，然而碳原子、氧原子组成二氧化碳分子时，原子的种类和数量都没有变，但总质量却减小了。整个过程除了释放了一定的能量之外，并没有发生其它的事情。

似乎是能量减少了一点，质量就会减少一点，就好像质量不是用来衡量组成物质的微粒，而是用来衡量能量的多少似的。

没错，这正是问题的关键：在狭义相对论里，质量确实变成了一个衡量体系能量多少的量。你静止时有多少能量，对应的质量就是多少，它们的关系由质能方程E=mc²给出。质量不是别的什么东西，它就是能量的量度，这才是一切问题的关键。

以前，我们老觉得质量是物质的代名词，觉得一卡车砖头的质量等于每一块砖头的质量之和，所以每一个分子的质量就应该等于所有组成它原子的质量之和。我们是如此地相信还原论，相信所有的物质都可以还原为一个个基本粒子，相信物质的质量等于所有组成物质粒子的质量之和。

而这，正是我们理解质能方程的最大障碍。

现在我们要改变观念，物质的质量不再是组成它基本粒子的质量之和，而是用来度量能量的。物质的能量固然包含了组成物质的基本粒子的能量，但它还包含了基本粒子之间因为相互作用而具有的能量，比如各种势能。

比如，什么叫重力势能？我搬起一块石头，石头就增加了一定的重力势能。因为石头和地球之间存在引力，当石头离开地面后，石头和地球之间就存在这样一种能量。石头落地后，重力势能减少了，度量能量的质量自然也跟着减小了，减少的能量E和质量m之间满足E=mc²。

质子和中子组成氘核的情况也一样，无非就是把质子和中子换成了地球和石头，把质子和中子之间的强力换成了地球和石头之间的引力，一个释放了重力势能，一个释放了核能。

因此，只有我们认为“质量是能量的量度”，而不再是牛顿观念里物质的代名词，不再是衡量物质所包含基本粒子的质量之和时，我们才能逻辑一致地看待上述所有问题，才能非常自然地解释质量亏损。

为什么质子和中子组成氘核之后，它们的质量会减小？因为独立的质子和中子具有一定的能量，而质量是能量的量度，所以质子和中子组成的系统就具有一定的质量。质子和中子组成氘核后释放了一定的能量E，系统的总能量减少了，度量能量的质量m自然也减小了，它们之间满足E=mc²。

木炭燃烧变成了二氧化碳，碳原子和氧原子组合成二氧化碳分子时释放了能量E，于是度量能量的质量m自然也减小了，它们之间依然满足质能方程E=mc²。

我用力拉开两个磁铁，其实是往磁铁组成的系统里注入了能量，磁铁的能量增加了，度量能量的质量自然也跟着增加了。所以，分开的磁铁会比吸在一起的磁铁更重，你用多大能量把磁铁拉开，它们的质量就增加了这个能量除以光速c的平方。

我们用力压缩一个弹簧，弹簧的能量增加了，度量弹簧能量的质量自然也增加了。所以，压缩的弹簧比松开的弹簧更重。

一个手电筒发出了一束光，因为光带走了一部分能量，所以手电筒的能量减少了，度量手电筒能量的质量自然也减小了。于是，发光手电筒的质量会一直慢慢减小。

但是，如果我们把手电筒放在一个铁箱子里，虽然发光手电筒的质量在不断减小，但手电筒发出的光并没有逃出箱子，所以手电筒和箱子的总能量并没有减少。于是，手电筒和箱子的总质量也不会发生变化。

为什么要举这么多例子？当然是帮你快速洗脑。

我们在牛顿的世界里浸泡了太久，已经形成了极大的思维惯性。当我们在谈论物理，谈论自然界的各种现象时，潜意识里就会从牛顿的角度来思考问题，所以我们会觉得相对论和量子力学很奇怪。所谓奇怪，无非就是跟固有的观念不一样，在这里就是跟牛顿的观念不一样。

17新的图景

我们要不断提醒自己：现在的物理图景已经不再是牛顿那样了，宇宙并不是一堆微粒的集合，一个物体的质量也不是组成物体实物微粒的质量之和。

如果你觉得“让人不这样思考”比较难，那可以接触一下量子场论，试着从量子场的角度来看待这个世界。毕竟，让人忘掉熟悉的旧观念很难，但是，一旦接受了新的观念，旧观念自然就忘了。

量子场论首先是一种场论，它的核心思想是：宇宙并不是由什么“实物粒子”构成的，而仅仅是由场构成，一切都是场。所谓粒子，不过是这些量子化场的激发态。

然后，量子场论是量子力学和狭义相对论联姻的产物。为什么我们要让量子力学和狭义相对论联姻呢？因为处理微观粒子要用量子力学，处理高速（近光速）运动的物体要用狭义相对论。那么，如果你想处理高速的微观粒子，就必须同时使用量子力学和狭义相对论，也就是它们联姻后的量子场论。

也因如此，当我们用量子场论看问题时，我们其实也是在用狭义相对论看问题。而质能方程又是狭义相对论的结论，所以量子场论的图景跟质能方程是相容的。

毕竟，如果一切都是场，没有什么“实物粒子”，那自然就不存在什么“实物粒子被摧毁了变成能量”的说法。如果一切都是场，各种物理现象就只是场与场之间的相互作用，不存在谁被摧毁了，自然也不存在什么代表物质的“质量”转化成了能量。

这样，“质量转化成能量”就完全站不住脚了。

而前面我们也说了，场是有能量的，场和场之间的相互作用自然会涉及能量的变化。能量在不断变化，度量能量的质量自然也会不断变化，它们的桥梁就是质能方程。

这样，我们就可以非常自然地接受“质量是能量的量度”这个观念了，而这，才是打开质能方程E=mc²的正确方式。

18不动的质量

不过，需要注意的是，我上面说的"质量是能量的量度"，指的都是物体静止时的能量，并不涉及物体的动能。

我们知道动能是跟参考系有关的，在一个参考系里是静止的物体（动能为0），在另一个参考系里可能就是运动的（动能不为0），动能并不一样。

因此，如果把动能考虑进去，速度的增加就会导致动能的增加，能量增加了对应的质量也会增加。这样，物体的质量就会随着速度的增加而增加，也就是所谓的动质量。

但是，我非常不希望引入动质量。物理学要把握变化世界里不变的东西，质量原本是跟物体的运动状态无关的，你现在让它随着速度的变化而变化，何必呢？动质量又不是非用不可，我的文章从头到尾都没有动质量，不一样可以讲质能方程么？

我知道，有些地方是从动质量开始讲质能方程的。他们先定义动质量，再把狭义相对论的新动量定义为动质量和速度的乘积，然后去算新动能。

这样读者就会很困惑，你凭什么把新动量定义为动质量和速度的乘积？难道狭义相对论就是用动质量替换掉原来的质量，剩下的照搬？然后各种脑洞大开，胡思乱想。

在这篇文章里，我只是坚持狭义相对论的基本原理，要求动量守恒定律在洛伦兹变换下保持数学形式不变，然后自然就得到了新动量：

这样逻辑上就非常自然。在这个新动量里，质量m依然是不随物体的运动状态而改变的质量，动量是一个速度的函数，而不是动质量和速度的乘积。

另外，我们再看一看狭义相对论的新动能：

爱因斯坦认为mc²是物体静止时的能量，E是物体的动能，所以γmc²就是物体的总能量（动能+静能）：γmc²=E+mc²。

现在我们说“质量是能量的量度”，如果这个能量指的是物体静止时的能量mc²，那质量就是（静）质量；如果我们把动能E也加进来，认为能量是总能量γmc²， 那得到的就是动质量。

也就是说，动质量和总能量在某种程度上是在描述相同的东西。然而，总能量是一直都存在的，并且是个非常重要的守恒量。如果已经存在一个守恒的总能量，为什么还要引入会导致混乱的动质量呢？

因此，我在文章里提到的质量通通都是（静）质量，完全不用动质量这种东西，也省得大家胡思乱想，最后把自己带沟里去了。

当然，虽然学界的主流是舍弃动质量，但也有少数学者认为动质量依然有存在的必要，这个我就不多说了，感兴趣的自己去查。

19结语

写到这里，文章差不多就可以收尾了。

通观全文，大家会发现质能方程的推导还是很简单的，只要遵守狭义相对论的基本原理，E=mc²就会自动地从动能表达式里冒出来。

真正困难的，还是理解质能方程背后世界观和物质观的转变，理解从牛顿到狭义相对论的转变，理解从“质量转化成能量”到“质量是能量的量度”的转变。

虽然相对论和量子力学革命已经过去了百年，但牛顿的观念还是深深地烙在许多人的心里。毕竟，我们在中学都要学习牛顿力学，只有少数人会系统地学习相对论和量子力学，而这方面的科普又比较少。

所以，习惯于用牛顿的观念去理解质能方程并不奇怪。

但话又说回来，毕竟如今已经是21世纪了，相对论和量子力学已经极大地改变了牛顿的世界观和物质观。如果你对后牛顿时代的物理学不感兴趣也就罢了，如果感兴趣（比如质能方程），就一定要注意牛顿观念的局限性。

我们不能总是从牛顿的角度来考虑这些后牛顿时代的物理学，否则，我们不仅无法掌握这些内容，还会误入歧途。

如果你能很好地理解质能方程，就能很好地理解狭义相对论，也能很好地理解从牛顿到现代物理的转变，这是一块非常好的试金石。

所以，现在你明白质能方程E=mc²了么？