下载客户端

大视场全息AR显示：锥形全息光学元件

2022-03-24 11:11

来源：澎湃新闻·澎湃号·湃客

撰稿 | 望舒

近期，元宇宙（名词解释>）概念的兴起，极大的推进了增强现实（AR）和虚拟现实（VR）技术的发展。为了进一步提升 AR 显示中用户与现实场景交互的 3D 沉浸式体验，解决辐辏和调节冲突以及视疲劳等问题，人们引入了全息显示（名词解释>）技术，该技术可以完整的重建出3D物体的波前信息，获得双眼视差（名词解释>）和连续运动视差（名词解释>），被认为是理想的 3D 显示技术之一。

然而，目前常见的全息 3D 显示所用的全息图都是平面的，如图 1 所示，用户只有在全息图正前方才能观察到完整的 3D 再现像，其他角度的视场都是受限的，甚至从全息图侧面、顶部、底部和正后方完全无法观察到全息再现像。这种限制源自于全息图的形状，在传统的平面全息图中是难以避免的。虽然有不少研究者提出了柱面全息图和球面全息图来克服这种限制，但是由于加载全息图的关键器件空间光调制器（名词解释>）难以实现非平面的结构，因此很难与柱面和球面全息图的理论达成共鸣，从根本上解决平面全息图的局限性。从实用的角度出发，如何在平面全息图的基础上实现大视场全息 3D 显示，成为了全息 AR 显示中最核心的问题之一。

图1：平面全息图的可视区域范围

基于此问题，日本大阪产业技术研究所 Yusuke Sando 和日本宇都宫大学光学研究中心的 Daisuke Barada 等人设计了一种锥形结构的全息光学元件（HOE）（名词解释>），并对它重构出的大角度发散球面波质量和光谱反射率都进行了研究。

他们介绍了这种锥形 HOE 的制作过程，并详细说明了基于费马原理的全息图计算方法，同时，他们利用锥形 HOE 透明的光学特性，通过全息 3D 再现像和现实场景的虚实融合实验，实现了大视场全息 AR 显示效果，其水平视角达到了 140°，垂直视角达到了 30°。

近期，该成果以 “Holographic augmented reality display with conical holographic optical element for wide viewing zone” 为题在线发表在Light: Advanced Manufacturing。

论文主要分为四部分内容：锥形 HOE 的光学性能研究、基于锥形 HOE 的大视场全息 AR 显示原理和实验、锥形 HOE 的制作以及基于费马原理（名词解释>）的全息图计算方法。

锥形HOE的光学性能研究

作者们首先研究了锥形 HOE 将垂直入射的平面波转换为向外发散的大角度球面波的原理和过程，如下图 2 所示，其中红色箭头代表入射的平面波，绿色箭头代表出射的发散球面波。球面波的最大发散角是由 HOE 记录过程时使用的物镜数值孔径(NA) （名词解释>）所决定的。经测量，设计的锥形 HOE 在仰角 θ 从 40° 到 80° 的范围内都能检测到发散球面波。

图2：锥形HOE的光学特性

此外，作者们还测量了他们设计出的锥形HOE的衍射效率和波长选择性。其中， HOE 的衍射效率和仰角 θ 有很强的相关性，在 θ 为 60° 的时候达到峰值。在这个峰值的条件下，他们测量了该 HOE 的光谱反射率，得到了在 532 nm 波长附近的尖峰，带宽约为 11 nm，刚好对应了锥形 HOE 记录时所使用的光波长。以上这些测量结果对他们实现大视场全息 AR 显示提供了必要的参考。

基于锥形HOE的大视场全息AR显示原理和实验

基于这种锥形 HOE，他们设计了一种大视场全息 AR 显示方法，其原理如下图3所示，激光通过透镜1形成准直光束，经计算全息图（CGH）调制后通过透镜 2，再经过反射镜反射后在透镜 2 的傅里叶平面上滤除掉杂散光，然后垂直入射到锥形 HOE 表面，从而以较大反射角反射到观察者眼中。如果基于锥形 HOE 的来设计和计算全息图，观察者就可以看到在锥形 HOE 内部重建的虚拟图像。

图3：基于锥形HOE的大视场全息AR显示系统

为了验证这种方法的可行性，如图 4 所示，作者们以线框立方体作为被记录物体计算全息图，以一个插在黏土里的螺钉作为现实场景，设计了一组大视场全息显示和现实场景虚实融合的光学实验。他们从不同的角度捕捉全息 3D 再现像，验证了大视场全息 AR 显示效果，如图 5 所示，随着观察角度的变化，全息再现像也发生了适当的变化。经过测量，该系统的水平视角达到了 140°，垂直视角达到了 30°。

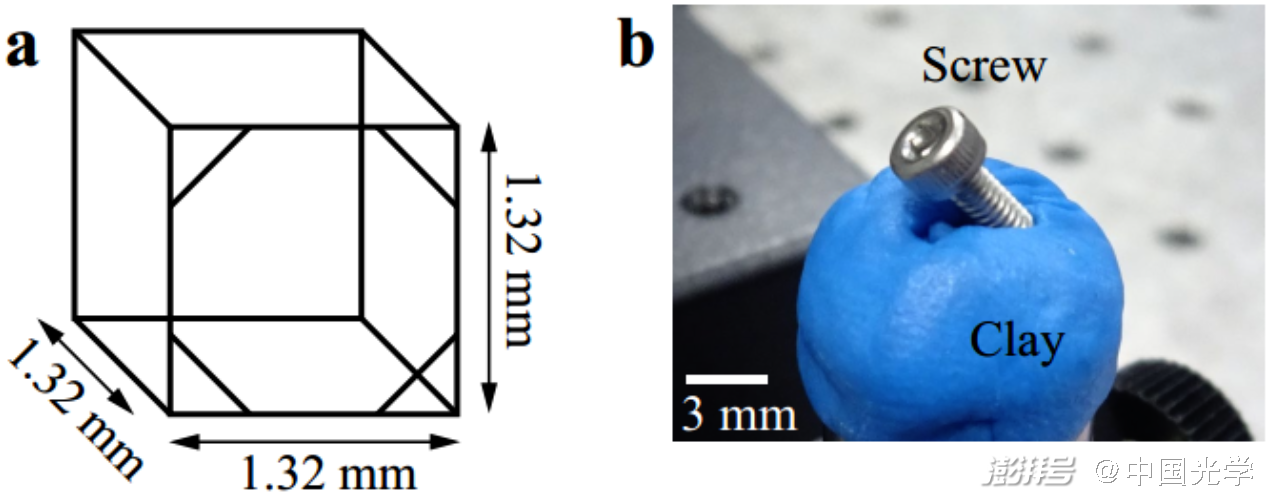
图4 所使用的虚拟3D物体和现实场景物体

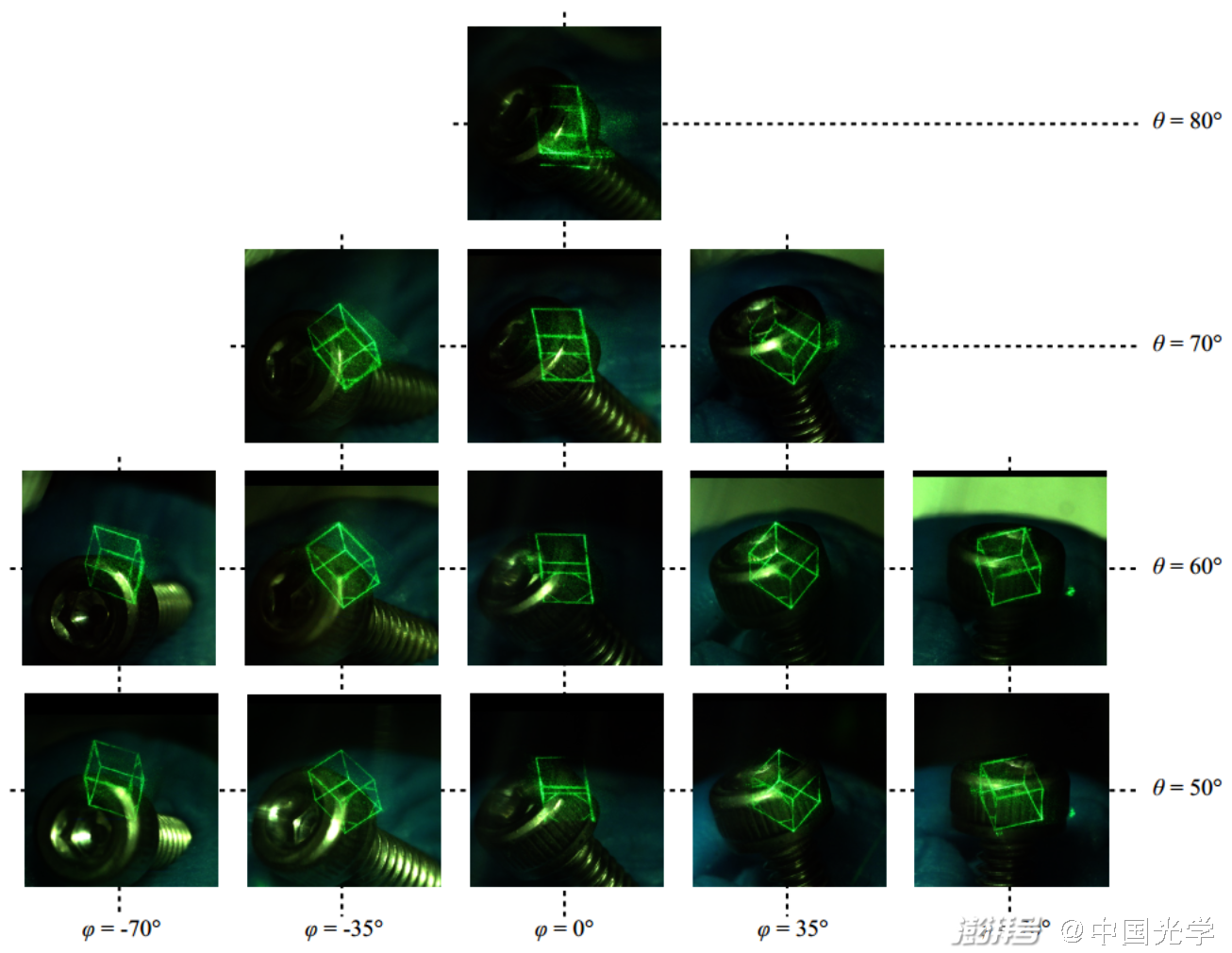
图5：大视场全息AR显示效果

在实验过程中，作者们还发现有些全息再现像发生了形变，畸变程度随重建位置和观察方向的不同而不同。他们认为这种畸变是由光学系统的误差导致的，尤其是锥形 HOE 的光学特性，这种误差有待进一步评估和修正。

同时，作者们还分析到，虽然他们提出的方法主要优势在于较大的观看视角，但是这个视角的最大范围还是要受到一些因素的限制。

其一是锥形 HOE 记录过程中使用的物镜参数，直接决定了 HOE 的最大发散角；

其二是入射波前照射在锥形 HOE 的区域范围，在图 3 所示的光学系统中，为了扩大横向观看视角，需要缩小计算全息图的像素间距或者使用大焦距的透镜。然而，与传统全息 3D 显示一样，再现像尺寸大小和视角大小之间仍存在制约关系，如果使用了大焦距透镜，就意味着再现像的尺寸被减小了，反之亦然。因此，增大计算全息图的空间带宽积是实现大视角和大尺寸的必要条件。在这点上，由于该系统所使用的的都是平面全息图，在进行多个空间光调制器拼接方面是有优势的。

此外，由于锥形 HOE 是旋转对称结构，水平视角原则上能达到 360°，该系统的水平视角仅有 140° 的原因是由于在透镜 2 的傅里叶平面上设置了空间滤波器来滤除掉杂散光，这也导致了锥形 HOE 仅有一半的区域被照射。如果利用复振幅编码来优化全息图算法，就可以优化掉空间滤波器从而使系统的水平视角达到 360°。

锥形HOE的制作方法

作者们简单介绍了锥形 HOE 的制作方法，其制备原理如图 6 所示，利用分束镜产生两束相干的平面波，一束作为参考波，另一束通过物镜形成发散的球面波，两束光波在空间中发生干涉效应，形成的干涉条纹被记录在锥形的光致聚合物的薄膜中。

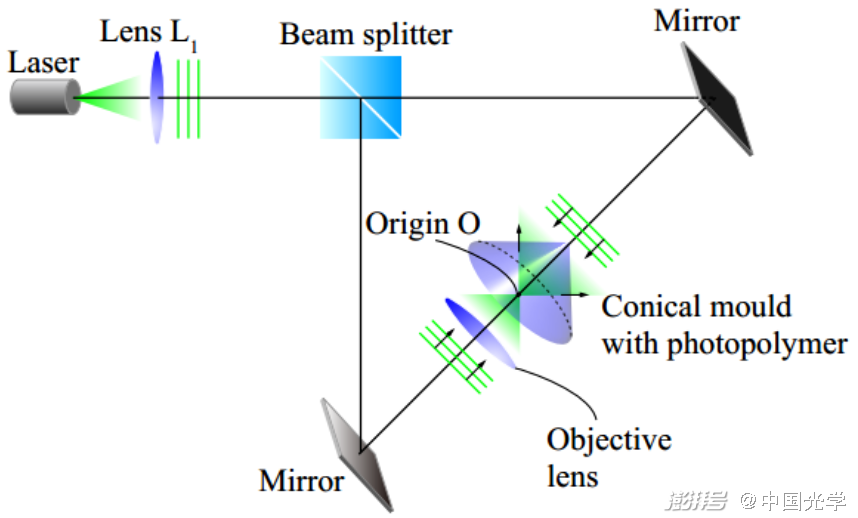
图6：锥形HOE的制备原理

基于费马原理的全息图计算方法

最后，作者们介绍了适用于这种锥形 HOE 的全息图计算方法，与以往传统的全息图算法不同的是，该系统的全息图的计算过程必须考虑到锥形 HOE 上的反射，因此基于几何光学中的费马原理，作者们推导出了新的全息图计算方法，如下图 7 所示，其中，重点是计算从物点 S 经过锥形 HOE 上反射点 R 到全息面像素 M 之间的光程。