探索素数分布有新进展：奥波曼猜想获证！

编者按：奥波曼猜想将新增素数间隔控制在了一个较精准的范围里，这是一个奇妙的猜想，比素数定理还要深刻。我们知道素数定理的证明是探索素数分布的一个里程碑，数学界能再创造新里程碑的是黎曼猜想、哥德巴赫猜想和奥波曼猜想等这些猜想获证，奥波曼猜想获证意味着素数分布人类又清晰了一层，它更加有利于人类精准捕捉后继素数。本文证明是关于素数分布的一次重要探索，它的重要突破是，大于6的所有偶数都存在共轭素数对，且共轭差非0，这是强伯特兰猜想，也是互素型歌德巴赫猜想，此猜想获证，奥波曼猜想就获证。

在证明强伯特兰猜想和互素型歌德巴赫猜想时，本文作者提供了两种证法，一是用反证法证明了，素数连加，如果不能通过更换一个新增素数构造可表偶数的相邻偶数，那么用任何素数连加都无法构造该相邻偶数，这与算术基本定理矛盾，从而反证强伯特兰猜想和哥猜成立；二是通过证明龙头例外偶数与可表偶数是相邻互素的，说明龙头例外偶数的素数因子须同所有的素因子累积互素，从而可证明无素因子可构造，例外偶数为空集，如此强伯特兰猜想和互素型哥德巴赫猜想就成立。以此做引理，奥波曼猜想就获证。

【摘要】素数相邻递增法则以及哥德巴赫猜想的获证，体现了等量变化和不等量变化是缔造数学大厦的基石，简易不易的思想原来一直贯穿着数学的始终。给定数的后继素数在梯度数域中存在， p=（n/2 ～ n-2）（n>6，且共轭于整数 n/2）。继而得到，在 x 与 x+ √x之间至少有一个素数，它比素数定理在判断素数分布时更精准。

【关键词】 伯特兰猜想；纯数学简洁证明；邻函数定理；哥德巴赫猜想；给定数的后继素数公式；杰波夫猜想；布罗卡尔猜想； 奥波曼猜想。

伯特兰猜想①：在 n 与 2n-2（n>6）之间至少有一个素数。该猜想切比雪夫已完成证明，在数论专著《数学底层引擎相邻论和重合法》里的“哥猜”一文中，本文作者还专门为伯特兰猜想添加了一个自创的初等证明。但该猜想还可进一步推广为一个更强势命题：在正整数后继有序一一映射素数的前提下（最小正整数对应最小奇素数，如 1 映射 3，2 映射 5，…，n 映射 p），n 与 2n-2（n>6）之间每次后继龙头偶数 2n 至少有一个紧邻的后继新素数 p 与之对应。即每一个后继龙头偶数所匹配的每一个后继素数，一定在 n与 2n-2（n>6）之间。就是说与自然数唯一匹配递增的后继素数一定落在 n 与 2n-2（n>6）之间。这与至少有一个素数的原伯特兰猜想不同，强伯特兰猜想表达了在已有素数两两相加不能构造新偶数时，具有唯一性的新增素数在这一后继区间必存在，才能用一对素数共轭构造新增后继偶数。强伯特兰猜想与两素数互异型的哥德巴赫猜想等价，比欧拉型哥德巴赫猜想略微强势，而欧拉型哥德巴赫猜想又比原伯特兰猜想强势。

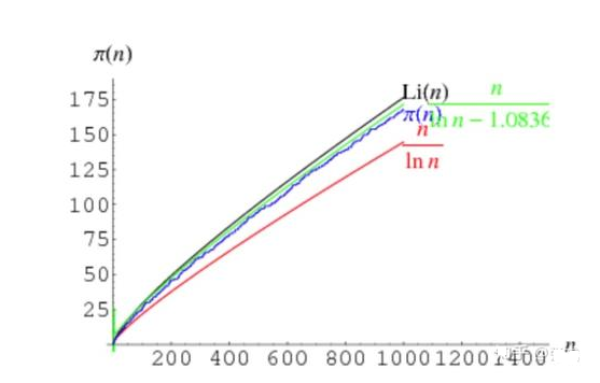
比素数定理更能精准捕捉素数分布

本书在其他论文中提到的相邻论和重合法是一种不同于矩阵和群论的数学工具，它是证明哥德巴赫猜想的关键。

比例研究的是自变量的曲率变化；间隔研究的是自变量的差值变化。比例和间隔的性态显示了事物的时空变化规律，可以用来预测和勘探。群论是从等量对称角度研究比例的；矩阵是从等量对称角度研究间隔的。重合法和相邻论则是从另一个角度，即用不等量非对称来研究比例概率和间隔梯度的。

尤其是用不等量研究素数相邻迭代变化的梯度学，作者在此领域获得了重大突破，用此工具有幸破解了哥德巴赫猜想，但本文证明，并不限于把哥德巴赫猜想成立作为引理，而是在算术基本定理的基数上进行证明。我们知道：统计是对概率的具体应用；筹算是对梯度的具体应用。

那么用重合法研究的统计、用相邻论研究的筹算，同近世代数相比有何根本的不同呢？关键在于新方法是从梯度的方向提出了算子码概念，从概率的角度提出了因子码概念，它们是余数和模数的统一。由此建立了可兼容集合论的序列论新数学体系，此是后话，本文不做展开。在此提一笔，意在相告能解决复杂数学问题的好工具定会带来数学发展的新前景。

1. 伯特兰猜想：在 n/2 与 n-2（n 大于 6）之间至少有一个素数

把 2n 代入 n，该命题可等价变换为 n 与 2n-2（n>3）之间至少有一个素数； 把 n+2 代入 n，该命题可等价变换为 n+2 与 2n+2 之间至少有一个素数（n>1）。

因为新增偶数与新增素数的差值都是 2，故可以继续等价变换为 n 与 2n 之间至少有一个素数；当 n 与 2n 之间没有新增素数时，n+2 与 2n+2 之间一定有新增素数，即一定有孪生素数产生。以上四个命题都等价于伯特兰猜想。

在此基础上，还可以推广得到强伯特兰猜想（即邻函数定理②）。每一个给定中值数 n/2 所匹配的每一个后继素数 p，一定包含在 n/2 与 n-2（n>6）之间，且以 n/2 为中心有互素的共轭素数。即 p=（n/2 ～ n-2）（n>6）。邻函数定理成立，伯特兰猜想就自然成立。

梅森素数

证明：现在就来证明邻函数定理。若给定偶数可表 2 项素数之和，则新增相邻偶数亦可表两素数之和。显然在给定偶数中其中大素数有上限，用一个大于上限的新增素数 p 新来更换其中一个素数，那么两素数之和 2p 大的相邻偶数2p 大 +2，可由一个新增素数 p 新同其≤ p 大的一个素数连和获得，即：

2p 大 +2=p 新 +p 小，或者 2p 大 +2 =p 新 +p 大

即（p 小 +p大）/ 2=n 可确定，n 是 p 小与 p 大的算术平均数，那么算术平均数n 一定会紧致地一一映射素数 pn，且 pn=（n/2~n-2）（n ＞ 6），或 2n=pn+p 小。总之，后继相邻偶数总可以由后继相邻素数参与的素数对连和获得。

下面就来证明这个邻函数定理。

已知“任意域奇素数 2n 项连和可获任意偶数”③，又因为有限域素数，其两两排列组合成的素数对有限，其两两相加所获得的不同值必有限，两素数之和一旦要获得大素数 2p 大 +2 的新增相邻偶数，须增加或更换新素数连和项。

2n=p1+p2+p3+p4+p5+…+p2n（2n 项连和）

我们还知道，所有偶数都是在给定偶数的基础上通过不断获得新增相邻偶数而产生的（皮亚诺公理）。而给定偶数的连和项是有限的，素数域是有限的。

假如 2n 或 2p 大为给定偶数，那么 2p+2=2+p1+p2+p3+p4+p5+…+p，还因为“任意域奇素数 2n 项连和可获任意偶数”，因此等式的右边可以表示成奇素数的连和，2 可以等价替换为奇素数。把 2 拆分成两个 1 加到素数中去，显然不行，那样素数项变成偶数项了。现更换 2 个新素数连和不能得到给定偶数的相邻偶数，新增相邻素数之比大于1 小于 2 ④，故更换 2 个或 2 个以上新增素数之和必大于新增相邻偶数，就算差值最小的孪生素数出现，它们的两倍之差是 4，也大于 2。可见更换 2 个或 2 个以上新增素数是不能获得相邻偶数的。那增加 1 项和 1 项以上素数参与连和是否能得到新增相邻偶数呢？也不能，因为最小的奇素数是 3，大于差值 2 的相邻递增。这就排除了新添素数项可获相邻偶数的可能，也排除了更换 2 个或2 个以上＞ p 大的素数项来获得给定偶数的相邻偶数。

但因为“任意域奇素数 2n 项连和可获任意偶数”，故不能排除给定偶数的相邻偶数可通过素数连和获得。因此给定偶数 2n 的相邻偶数 2n+2，可由一个新增素数 p 新同其≤ n（n可取p 大）的一个素数连和获得，即：

2p 大+2=p 新 +p 小 或 2p 大+2=p 新 +p 大

也就是说素数连和连积恒等式已证明存在偶数个素数连和是可以得到全部偶数的（另文有 6 种方法已经完成证明），因此，经过可穷分类（n ≥ 2，n=1，n=0）的头尾两项排除后，剩下中间 n=1 的唯一选项无法排除，“偶数个素数连和项中只有轮值⑤更换一个新增素数方能取得一组相邻偶数”。

其中偶数的 1/ 2 有映射素数的叫龙头偶数，龙头偶数的后继相邻偶数必须寻找大于映射素数的新增素数，参与跟已获素数两两相加才能得到。总之，任意偶数的后继偶数都需要寻找大于原偶数的 1/ 2 的新增素数，同小于原偶数的1/ 2 的已获素数两两相加得到。有新增素数就一定有新的龙头偶数；有新的龙头偶数就有新的龙头相邻偶数⑥；有新的龙头相邻偶数就有更新的新增素数。如此循环不断，此判定就是素数两两相加产生所有无限连续偶数的充分必要条件，结合算术基本定理，可以证明素数的无穷性特征，这是不同于欧几里得和欧拉完成的另一种素数无穷性证明，故相邻论表达式成立。具体见本书第一篇论文 3.5。以上邻函数定理得证。

除了递增相邻表达的邻函数定理；还有递减相邻表达的邻函数定理。较大素数 p 大 +3-2 即素数加 3 的递减相邻偶数，必不能用 p 大及其域内素数相加获得，而是要用递减相邻素数及其域内素数相加才能获得。

若给定偶数可表 2 项素数之和，则其中递减相邻素数有下限，用一个小于下限的递减素数 p 小来更换其中一个素数，那么两素数之和 3+p 大的相邻递减偶数 3+p 大 -2，可由一个递减素数 p 小同其≤ p 小的一个素数连和获得，即：

3+p 小 -2=p 小 +p 更小，或者 3+p 大 -2=p 小 +p 更小 这是邻函数定理的递减表达，证明同上。

2. 2k 个奇素数连和定能得到不小于 8 的全部偶数

从邻函数定理得知，因为新增素数大于 n，说明总存在大于 n 的素数同小于n的素数相加，可获得2n的相邻偶数2n+2，如果让相邻偶数跑遍所有的偶数，就可得到，所有的偶数在素数对的偶数项连和中都可以通过更换一个大于算术平均数即中值数 n 的新素数来同小于中值数 n 的原素数连和获得。

由于所有的相邻偶数，都是通过大于中值数 n 的新素数和小于中值数 n 的原素数相加获得的，说明“任意域奇素数 2n 项连和可获任意偶数”，都是其中一项素数变量产生所有偶数的。也就是说，“任意域奇素数是先有 2 项连和可获任意偶数”，而后才有“任意域奇素数 2n 项连和可获任意偶数”的。

假如“任意域奇素数 2 项连和不能获得不小于 6 的任意偶数”，那么偶数有限项连和或无限项连和也不能获得任意偶数。因为偶数有限项连和只是一个可确定的给定常数，素数 2 项连和不能获得所有偶数，素数 2 项连和加常数2m 也就同样不能获得任意偶数。但因为“任意域奇素数 2n 项连和是可获任意偶数”的，故“任意域奇素数 2 项连和就定能获得不小于 6 的任意偶数”，后者是前者的充要条件。正如火车能跑是因为火车头能跑。这就是相邻论。

该结论证明了，2k 个素数连和定能得到全部偶数，2k 为定值，且每次获得 2p 的相邻偶数 2p+2 时，只能更换一个新增素数才能连和获得新增相邻偶数。该结论说明了，任何一个素数的 2 倍之相邻偶数，都需要更替一个且仅需更替一个新增素数参与连和获得。我们把形如 2p+2 的相邻偶数叫龙头相邻偶数。我们把形如 2n+2 的相邻偶数叫任意相邻偶数。

3. 龙头相邻偶数都可以通过后继素数或更大的后继素数参与的素数对之和获得

要获得龙头相邻偶数一定需要大于 p 的新素数对参与连和才能获得。要获得任意相邻偶数一定需要大于中值数 n 的新素数对参与同小于中值数 n 的原素数连和才能获得，因为当 n 是偶数，或者是非素数的奇数时，都需要大于 n 才能得到素数，其他选项都形如 2p+2。也就是说只要有 n 递增获得任意相邻偶数，就有新素数对递增，只要有龙头相邻偶数递增，就有确定的新增素数递增，而不仅仅是新素数对递增。广义上也就是说，任何一个自然数 n 的 2 倍之相邻偶数，都需要更替一个且仅需要轮值更替一个大于 n 的素数参与连和才能获得。这是相邻论的核心， 这个结论证明了，2n 的相邻偶数一定需要大于 n 的素数连和才能得到。

这个判定就是强伯特兰猜想。同原伯特兰猜想不同点在于，强猜想将“至少有一个素数”的不明确性扩展到“不仅包含有无穷个新素数，且包含有无漏个紧致相邻素数”，关键是还共轭于中值数。

素数间隔波谲云诡

当然大于 n 的素数不一定都是新增素数，但大于 n 的素数与小于 n 的素数会出现新增两两组合的素数对，其中部分素数对之和会出现新增相邻偶数，当n=p 时的 2n 相邻偶数 2n+2，则一定会出现新增素数对。每一轮新增素数的产生都需要相邻偶数的多次递增。此时新增素数与原素数进行新的两两组合（其个数为C(n+1, 2 ）)就会产生新增素数对，其中素数对之和有大于 2n 的也有小于 2n 的，大于 2n 的就构成了新增相邻偶数。显然 n 的相邻递增总能带来素数对的无漏相邻新增组合。

由此可知，2n 必至少有一对共轭数定是共轭素数，因为 2n 的每一个相邻偶数都需要一个大于 n 或大于等于 n+1 的素数参与连和才能获得。用排除法进一步证明这个结论，任何 2n+2 都至少由一对共轭素数相加获得，可见不小于8 的偶数都可以用非 0 共轭差的素数对之和表示。偶数 6 只能用相同的素数对之和表示。这个结论比欧拉版的哥德巴赫猜想还要强势得多。这意味着用自然数个数所全部对应的素数两两相加可得到全部偶数。正是因为这个强结论，哥德巴赫猜想才比黎曼猜想要强一些。

最后总结下强伯特兰猜想即邻函数定理的三个要点和关键证明步骤：

（1）在 2 项素数连和中，（含用 n-1 个较小素数冲抵大于中值数 n 的素数）每项素数任意用不大于中值数 n 的素数连和无法获得中值数 2 倍或 2n 倍的相邻偶数。此为老路够不着。（k=0）

（2）在 2 项素数连和中，（含用 n-1 个较小素数冲抵大于中值数 n 的素数）其中用 2 项或 2n 项大于中值数 n 的素数参与连和，无法获得中值数 2 倍或 2n倍的相邻偶数。此为邪路过了头。（k ≥ 2）

（3）素数连和项中，（含用 n-1 个较小素数冲抵大于中值数 n 的素数）须且仅须轮值一个素数变量更换为大于中值数 n 的新增素数再参与 2 项或 2n 项素数连和，方可获得无限连续偶数。否则就没有素数连和能构造 2n，但这会与算术基本定理判定任何偶数都可以用素数连和构造相矛盾。可见中和之道方可行。（k=1）

另外补充一点，n-1 奇数个素数必须能冲抵一个素数，否则素数多项式就不能包含可表偶数，如此就不能表达所有偶数，于是矛盾。故素数多项式必须蕴含素数二项式，且素数二项式必须能表达可表偶数的后继偶数，否则素数多项式就有偶数子集不能表达，于是矛盾。故邻函数定理条件必须成立。

经过可穷分类（把差值 2 拆分成两个 1 分到原素数对连和的两项中，这显然不行，素数变成偶数了；更换 2 个以上新增素数以及一个都不换，都是对差值不作为，已排除；把差值 2 不拆分轮值添加到原来其中的一项中，使其原来的一项变成新增素数，或更替一个新增素数，使差值 2 隐含在其中，这个无法排除），那么该剩下的无法排除的选项在邻函数的条件下就必须成立，即偶数项素数连和是一定能够获得无限连续偶数的。有限间隔项素数连和可进一步确定为偶数项素数连和，奇数项的素数连和必为奇数。因此所有偶数必定是偶数项素数连和获得的。根据相邻论的结论，素数连和项中，须且仅须轮值一个素数变量更换为大于中值数的新增素数再参与 2 项或 2n 项素数连和，方可获得无限连续偶数。

这一定理可以反证出 2 点：一是新增素数必须无穷，二是新增素数必须无漏。无穷地落在梯度域中为伯特兰猜想，无漏地落在梯度域中为强伯特兰猜想。若素数有穷，任意延伸的相邻偶数无法获得，矛盾；若素数有漏，每一延伸的相邻偶数无法获得，矛盾。

绝大部分龙头相邻偶数都可以通过后继素数参与的素数对之和获得，个别需要后继素数的后继素数参与才能获得，比如：31 的龙头相邻偶数是 64，31 的后继素数是 37，但 37 参与的素数对之和无法获得 64，需要 31 的后继素数的后继素数 41 参与的素数对之和，才能获得 64。41 的龙头相邻偶数是 84，41 的后继素数是 47，47 参与的素数对之和（与37 配对）可以获得 84，31 的后继素数 37，此时补了回来。更确定的是，可以在给定数范围内获得，作为中值数的 31 到 36 都在给定数范围，其后继素数都是 37，中值数 32 的相邻偶数 66 就是靠 37 参与的素数对之和获得的。通过素数对之和获得偶数全集的无穷素数一定是无漏素数，这丰满了哥德巴赫猜想的判定。强伯特兰关系用无穷无漏递增的素数两两相加表达了所有偶数。如果素数有漏，无须所有素数参与就能两两相加获得所有偶数，那么该有漏素数的 2 倍之对应偶数 2p，就被其他的素数对之和表达了，而该素数对的中值数定是奇数 n，因为若是素数，就不会漏掉，这就与对应偶数 2p 的中值数是素数 p 相矛盾。

因此通过新增素数两两相加获得所有偶数，就一定囊括了所有奇素数。回顾证明关键是，为使所得推论不与 p1+p2+p3+p4+…+ p=2n 相冲突，推论“偶数个素数连和项中只有轮值更换一个新增素数对才能取得无限相邻偶数”就必须成立，也就是说获得 2n+2 的素数对之和，都是轮值更换一个大于 n 的后继相邻新素数或素数对新组合才产生的。即不小于 8 的偶数，皆可表为两个不同素数之和，就必须在多项素数的连和中优先成立，因为每次获得新增相邻偶数时候，素数对仅有一个素数迭代变量在发生有效作用。这样一来素数连和只有两项成立才会多项成立。

其中 p+q=p1+q1+p2+q2+p3+q3+…+pi +qi 为同构等式的证明关键步骤是：

第一种情形，因为根据伯特兰―切比雪夫定理 n+1 与 2n+2 之间只能用一个大于 n+1 的新增素数做加项来构造中值数的 2 倍之偶数，用 1 个以上或等价于用 1 个以上新增素数肯定不行，会大于 2n+2，过犹。

第二种情形，用 1 个以下或等价 1 个新增素数都不用也肯定不行，不用或等价于不用新增素数，将不能构造 2n 及其后继偶数，会小于 2n+2，不及。可见两类表达式的初项取相同素数时，素数二项式若不能表达可表偶数的后继偶数，素数多项式也不能表达。

第三种情形，即令两类表达式的公共项素数（含合并等价）各有一个且都大于中值数，那 kq 中的 k 要求不等于 1，就意味着不能用（n+1）/ 2 与 n+1 之间的素数构造 2n+2，用 1 个以上或等价于用 1 个以上下线素数肯定不行，会大于 2n+2，过犹。于是就不存在关于中值数的 n+1 的共轭素数对，于是也就无法通过一对共轭素数相加构造 2n+2。

第四种情形，用 1 个以下或等价于用 1 个以下下线素数肯定也不行，会小于 2n+2，不及。同样无法通过一对共轭素数相加构造 2n+2。 

此方法获证的关键是，若不能更换一个新增素数，获取可表偶数的相邻偶数，便无法用任何线性映射的方法获取可表偶数的相邻偶数，用有界的二元素数基底进行线性映射不能无漏无限获得新增素数因子，而可表偶数的相邻偶数是一定能产生新增素数因子的，否则与三元方程两两互素矛盾。p+bq=2h,p、q为奇素数，当例外偶数每个定值都须b≠1时，偶数的最小相邻间隔会大于2，如此就无法构造所有偶数，这与算术基本定理会矛盾。推广后的强伯特兰猜想获证意义重大，为堆垒数论开辟了一个新方向。强伯特兰猜想所给出的是素数梯度确界值，它同概率确界值不同，梯度的显然精准，概率的只代表平均意义上存在。原伯特兰猜想虽然得到了切比雪夫和拉马努金的证明，甚至它的某些加强版也得到了证明，如：

定理 1：对任意自然数 n > 6，至少存在一个 4k+1 型和一个 4k+3 型素数 p， 使得 n < p < 2n。

定理 2：对任意自然数 k，存在自然数 N，对任意自然数 n > N ，至少存在 k 个素数 p ，使得 n < p < 2n。

但这些加强版都没有囊括所有素数，皆所指某一类无穷素数，同强伯特兰猜想比起来依然较弱。强伯特兰猜想成立，可以直接推导哥德巴赫猜想成立，而原伯特兰猜想以及部分加强版都不能做到这一点，仅被哥德巴赫猜想所证明，不能反推逆命题也成立。

有了强伯特兰定理做引理，以下可将杰波夫猜想（勒让德猜想）、布罗卡尔猜想、奥波曼猜想三个猜想一锅端。

1855 年，杰波夫（Jepov）认为，在 n^2 和 (n+1)^2 之间一定有两个素数，这就是杰波夫猜想。1905 年，迈伦特证明了对于比 9000000 小的平方数，杰波夫猜想成立。法国数学家布罗卡尔（Brocard，1845-1922）认为在两个素数的平方之间至少有 4 个素数，例如：在 9 和 25 之间有素数 11，13，17，19，23，这个命题既没有被证明，也没有被推翻。

4.用例外偶数是空集来证明强伯特兰猜想

令 2m（含 2p 亦含 2^w）为互异型可表偶数，互异型可表偶数就是能用两互异奇素数之和表达的偶数，2p´为例外偶数，例外偶数就是不能用两互异奇素数之和表达的偶数，p、p´为互异奇素数，它们的并集须囊括所有奇素数q。那么必有 2p´-2p=2t ，p´与 p作为单素数因子因互异而互素，根据三元方程若两元互素必三元两两互素的性质，p与t必累积互素互异，p´与t必累积互素互异。由于构造t的素因子始终要与p及p´互素，其累积结果，导致要与所有的奇素数q互异而互素，初项t与每个q（所有素数）皆互异而互素乃必要条件，如此t就没有奇素因子可构造，加上2p´-2^w =2t ，t与偶素数2也互素，故例外偶数2p´不存在。从而证明所有素数2p都是可表偶数，皆能用两个互异的素数之和表示。从而也证明了，可表偶数2m蕴含了所有的素数因子。

而龙头例外偶数2h，要么同可表偶数2m中的m1互异而相邻，相邻而互素，且不能等于m2，也不能等于m3，…，mi，这就要求与它们逐个皆相邻互素，因为不能等于其中任意一个mi，只能全部相邻互素一遍，h是同一个可表偶数并集U（mi）相邻互素，其中i∈1~n，于是例外偶数2h中的h，与可表偶数2m中的m须累积互素。而可表偶数2m全集是蕴含所有素数因子的（已证2p是互异型可表偶数，故m含所有奇素数因子p，8是可表偶数，故m也含偶素数因子2），故h与m累积互素的结果是，h无素数因子可构造，龙头例外偶数不存在，后继例外偶数也就不存在，于是例外偶数2h为空集。于是强伯特兰猜想和互素型哥德巴赫猜想就获证。互素型哥猜获证，就可证明很多相关猜想。

素数共轭互异对称

5. 杰波夫猜想（勒让德猜想）

现求证：p=n^2 ~（n+1）^2（n>1），p至少有两素数。（杰波夫猜想，也叫勒让德猜想，前者认为含两素数，后者认为至少含一个素数，因此杰波夫猜想更强些）。

n^2~（n+1）^2 之间的差值等于 2n+1。强伯特兰猜想已经证明，n 与 2n-2 之间至少有一素数，且以中值数 n 为中心共轭存在素数。

根据强伯特兰猜想，当 n-1 为共轭素数对的中位数时，必有 p1-p2=2n-2，两素数的间距大约等于 2n-2，即两素数之差可以获得 2n，2n 间距可以获得一个素数，超过这个间距 2，就需要新素数参与同小素数连和才能获得，因此2n+1 的间距就意味着有两个素数存在。

已知（n+1）^2 =n^2+2n+1，变换可得（n+1）^2-n2=2n+1，因此两个相邻数之间的平方差等于 2n+1，这意味着中位数 n 的两边即 n/2 以外 n 以内和 n 以外 2n以内各有一素数，也就是 n^2 以外 n^2 +n 以内和 n^2 +n 以内 n^2+2n 以内各有一个素数，当然 n^2+2n+1 以内也成立。另外，根据已知获证的斋藤猜想判定两素数的间距可以是任意偶数 2n，也可证明相邻整数的平方之间至少含两素数。如此这般杰波夫猜想就得到了证明。

6. 布罗卡尔猜想的证明

布罗卡尔猜想也可以同理证明。

已知素数加相邻差值的平方进行二项式展开可得：

（p+d）^2 =p^2+2dp+d^2  变换为：（p+d）^2-p^2=2dp+d^2 因此 两个相邻素数之间的平方差等于 2dp+d^2； 由于 素数相邻差至少大于或等于 2； 故 2dp+d^2 可以至少分成 2 个 2n+1； 又已知获证的斋藤猜想判定两素数的间距可以是任意 2n，伯特兰─切比雪夫定理也显示，n/ 2 与 n-2 之间以及 n 与 2n-2 之间各有一素数；因此 2n+1 显然就包含两素数；而 两素数的平方大于 4n；可见 两相邻素数平方差之间一定包含两对素数；即 四个素数，它们有两对差等于 2n。 如此这般布罗卡尔猜想就得到了证明。

1882 年奥波曼（Oberman）提出的猜想，在 x 与 x+ √x之间至少有一个素数， x 为可开平方数，或者修改为在 x 与 x±√x之间至少有一个素数。杰波夫猜想也叫勒让德猜想，但结论更强，杰波夫猜想获证，也就意味着奥波曼猜想可以归谬获证，因为它是杰波夫猜想的一般化推广，却是斋藤猜想的推论，是哥德巴赫猜想的推论，是相邻论的推论。

7. 证明奥波曼猜想

奥波曼猜想：在 x 与 x+ √x之间至少有一个素数，x 为可开平方数。用a^2+a 替换以上表达，a^2+a 与 a^2 之间是否存在素数就成了比杰波夫猜想或布罗卡尔猜想条件更严苛的推广。

奥波曼猜想比杰波夫猜想更精细，显然其判断更强，虽不能由杰波夫猜想成立而直接演绎导出，但可以因杰波夫猜想成立而反证出奥波曼猜想成立。

素数分布节奏难定

a^2 +a 将 a^2 到 (a+1)^2 之间分成了两部分，一部分是 a^2 +a 与 a^2 ，一部分是 a^2 +a 与 (a+1)^2 之间。根据杰波夫猜想已经证明 a^2 到 (a+1)^2 之间存在两个素数，如果 a 碰巧也是素数的话，a^2 到 (a+1)^2 之间就存在四个素数，布罗卡尔猜想刚已经证明了。如果不是素数，就存在两个素数，杰波夫猜想已经完成了证明。

若 a^2 +a 与 a^2 之间不存在素数，根据杰波夫猜想，a^2 +a 与 (a+1)^2 之间就一定存在两个素数，将 (a+1) 假设为 x，a^2 +a 就等于 x^2-x，(a+1)^2 就等于 x^2，因此 a^2 +a 与 (a+1)^2 等价于 a^2-a 与 a^2 之间。如果把猜想推广到正负素数中，a 取负数，其结果“a^2-a 与 a^2 ”与“a^2 +a 与 a^2 ”是等价的，故： 若 a^2 +a 与 a^2 之间不存在素数，那么 a^2-a 与 a^2 之间也不存在素数； 若 a^2-a 与 a^2 之间不存在素数，那么 a^2 +a 与 a^2 之间也就不存在素数。

但事实是 a^2 到 (a+1)^2 之间至少存在 2 个素数，杰波夫猜想已经证明了这一点。因此“a^2-a 与 a^2 ”与“a^2 +a 与 a^2 ”两段都必须至少各有一个素数。于是奥波曼猜想就获证。因为a^2 =x，可转换表达为（x+ √x）与x之间至少有一素数。

因为用√a 作为a代入 a^2 ，客观上缩小了 a^2 与 a^2 +a 之间的差值范围，故存在例外，如 8 与 8+ √8之间就没有素数，114 与 114+ √114之间就没有素数，故 a 为可开平方数时猜想才生效。当然 a 取任意数时，a 与 a+ √a之间一个素数都没有的情况是极少的。是不是超过某定值后就没有例外，还不得而知。但表达式通过调整，a 取任意数时，a 与 a±√a之间则定有素数。

以上猜想的获证，显示了离散量都可以用相邻量进行阶段性描述，相邻自然数之所以存在是基于有等量 1 的存在，如此非等量就可以用等量来描述，离散就可以用相邻来描述。等量关系存在是可认知的基础。爱因斯坦说，这个世界最不可理解的就是这个世界居然是可理解的。但习惯性的可理解方式会阻碍我们认识新的未知世界，这个时候，我们需要对原有的等量关系求变，只有用更细微的等量关系替代才能解决这一困境。这样一来，原来的等量关系打破了，所有的等量粒子都变得有区别性。因此等量关系是一种暂时的认可。没有一劳永逸的等量关系。离散量之所以可以用相邻量描述是因为，被假定有等量关系存在，若仍无法描述，需要去寻找更深刻的等量微粒子。如此这般无穷无尽才能认知宇宙，这个世界根本来说是次第的，平等是阶段性幻觉。（罗莫）。

参考文献

[1] 纳森 . 加性数论（经典基）：英文版 [M]. 北京：世界图书出版社北京公司，

2012.

[2]里本伯姆 . 博大精深的素数[M]. 孙淑玲，冯克勤，译 . 北京：科学出版社，

2007.

[3]R.K. 盖伊 . 数论中未解决的问题 [M]. 张明尧，译 . 北京：科学出版社，

2007.

[4] 罗莫 . 用重合法可证明哥德巴赫猜想原题 [J]. 数学学习与研究，2013

（3）：93-95.

注释：

①伯特兰猜想。伯特兰—切比雪夫定理说明：若整数 n>3，则至少存在一 个质数 p，符合 n<p<2n-2。另一个稍弱说法是：对于所有大于 1 的整数 n，存在一个质数 p，符合 n<p<2n。1845 年约瑟 • 伯特兰提出这个猜想。伯特兰检查了 2 至 3×106 之间的所有数。1850 年切比雪夫证明了这个猜想。拉马努金给出较简单的证明，而保罗 • 艾狄胥则借二项式系数给出了另一个简单的证明。

②邻函数定理。描述了整数在加法运算与乘法运算之间的关联，自然数与素数之间的谐波。它用构造性的方法通过素数逐级任意连和、素数逐级任意连积获得全部自然数，它是通过自然数相邻变化定点精准求解素数相邻变化的一个关联函数表达公式。

③“任意域奇素数 2n 项连和可获任意偶数。”这是作者在其他论文中完成证明的一个定理，它是算术基本定理的一个推论。自然数 n 可表为 p1p2p3p4… pn=mk，k 可以确定为所有的自然数 n，m 为素数或素数的乘积。k 可以分割成任意素数 p 加一偶数 2m1，mk 就可以表示成 m(p+2m1)，由于 2m1 可以分割成若干素数之和，m 可以理解为素数的个数，p 为所有参与的素数。因此所有素数参与的连和，一定可表自然数 n。

算术基本定理

推论 1，任意域奇素数 n 项连和可获任意正整数。

推论 2，任意域奇素数 2n 项连和可获任意偶数。

推论 3，任意域奇素数 2n+1 项连和可获任意奇数。

④相邻素数之比大于 1 小于 2，可以通过概率求证。根据素数定理， pn=nlnpn，因此相邻素数之比自然就是，p（n+1）/pn=（n+1）lnp（n+1）/nlnpn，对这个 比例求极限，可以求出相邻素数之比的平均数。

⑤轮值。鸽笼原理的体现，在自变量一元、因变量多元的函数表达式中， 其中多元因变量中会轮值其中一元同一元自变量一一映射。这种必有且仅有一项中彩的鸽笼原理效应，在多元不定方程中得到印证。多项素数连和可以获得任意偶数，但真正有新增素数参与的只有一项。

⑥龙头相邻偶数。第 n 个偶数同第 n 个素数有一一映射关系，因此偶数的递增会带来相应的素数的递增以及素数的新组合，其中能带来素数递增的相应偶数，叫龙头相邻偶数，算术平均数是素数时所对应的相邻偶数是龙头相邻偶数，这样的偶数需要新增素数参与相加才能获得。