费马猜想真有简洁证明： 本原解化约律和幂尾数周期律

编者按：这是一篇关于费马猜想的简洁证明，作者证明了两个引理，一个是洛书定理，即幂尾数周期律，同时还证明了本原解化约律，这是一种回归本质范畴的优化运算规则，就是把解集归属到更大范畴中去，找到解集成立的必要条件是幂尾数周期律。由两个引理可直接推出费马猜想成立。该猜想的证法，后来发现跟怀尔斯的证明很相似，怀尔斯是通过证明谷山-志村猜想以及弗赖猜想（已获证的肯.黎贝定理）来完成证明费马猜想成立的，谷山-志村猜想讲的是，椭圆方程若有解（M-序列）必可模形式（E-序列），也是将解集归属到更大范畴中去。其简化归属过程是证明关键，它是通过三大方法整体实现的。一个是科利瓦金方法，另一个是弗莱切方法，再一个是岩沢理论，三者协同完成了约化归属映射的证明。弗赖椭圆方程不可模形式，故弗赖椭圆方程不是有解的椭圆方程。

本文作者给出的证明，也用到三个方法，碰巧与怀尔斯的三个方法功能类似，一个是一次方的三元方程升幂后必变不等式，另一个是二次方的三元方程升幂后必变不等式，再一个是三元不等式除了一次方的升幂会变成有解方程外，其它的升幂后仍是不等式。本文作者的证法妙在找到了如何归简的思路，然后通过排除无法归简的集族，从而得到命题的精准证明。看得出这个证明方法与证明希尔伯特第八问题的思路是一致的，都是通过寻找最简本原解来解决问题的，其实同怀尔斯的解题思路也非常吻合。作者解决希尔伯特第八问题的文章最近发布在澎湃新闻上引起巨大反响，不到3天阅读量50多万，累积3篇过100万点击，可见读者对相邻论和重合法甚为关注，它不是一个仅解决孤立问题的方法，相反，它可相邻迭代指向不断升级的“通用性”，“普适性”，是解决数学难题的核心引擎。

重合法持还原论世界观，还原论指导我们，欲知“万物之理”，首先要由外而内一层一层地去探究事物的本性，再由内而外一层一层地建构宇宙的秩序，凡所给对象可同构同态认知，在数学领域大多有通项表达式（真相只有一个）。而相邻论则持演生论世界观，演生论告诉我们，在不同的尺度下，宇宙万物有着不同的本性；不存在唯一的“万物之理”（通用和普遍须不断升级），因为宇宙万物都是在演化的进程之中“涌现”出来的，而“涌现”是不确定的和不可一劳永逸预测的，凡所给对象可互异互素认知，在数学领域并无通项表达式，但存在相邻迭代表达（真相不止一个）。重合法有统一的周期律，而相邻论则有互异的约化律，所给对象皆可“阴符”于一个前继的更大范畴中，或皆可“阴符”于一个后继的更小范畴中。“阴符”就是暗合，就是约化，互异本性之间存在着梯度归属。怀尔斯证明费马猜想的一个最大收获是，诞生了高阶数学归纳法，由E-序列可探寻M-序列，由M-序列可探寻E-序列，由前继序列可探究后继序列，由后继序列可探究前继序列。也就是说可确定的集合概念定是潜在的普遍概念。

【摘要】 用洛书定理①的幂尾数周期判定法则，以及不等式和方程的维度升降法可证明费马猜想成立，印证了当年费马自称有一个巧妙证明只因《算术》一书的边角太小而写不下之类的话。另用此工具可进一步证明比尔猜想②，这是怀尔 斯③的模形式和椭圆曲线工具目前所不能完成的。

【关键词】 费马猜想；比尔猜想；巧妙证明；洛书定理；幂尾数周期律；一次与二次三元方程升幂变换 三元不等式升幂变换；费马无穷递降法。 

用洛书定理的幂尾数周期判定法，以及不等式和方程的维度升降法可证明费马猜想成立，印证了当年费马自称有一个巧妙证明只因《算术》一书的边角太小而写 不下之类的话。另用此工具还可进一步证明比尔猜想和考拉兹猜想成立，这是怀尔斯的模形式和椭圆曲线工具目前所不能完成的。作者发现的该方法与费马小定理及费马无穷递降法有异曲同工之妙。它与重合法和相邻论也是一致的，幂尾数周期判定规则和费马小定理是重合法，不等式和方程的维度升降法和无穷递降法以及数学归纳法是相邻论。重合法找到公共交集，找到全体并集，找到公约周期，找到连续同类；相邻论找到公共交集通往完美并集的梯度，找到离散异类，找到次第超越，找到化约律。 

此法果真很有威力，费马当年自称有一个巧妙证明原来不是吹牛！嘲讽费马吹牛的段子很多，例如：“我有一个巧妙证明，可惜我要下飞机了，没时间说”，“我有一个巧妙证明，可惜我妈喊我吃饭了，下回说”。其实费马真有卖关子的习惯，很多同时代的数学家都很恼火费马对数学发现的保密，不像现代人，一有发现，就想着立马向公众表白，生怕晚了丢了首发权。费马不在意这些，是否能发表，能否被承认，人家压根儿无所谓，他喜欢享受天下皆暗我独明的乐趣，直到他乐意了，他才抛几个数学发现出来，与大家共乐一番。因此费马没吹牛的概率极大。怀尔斯所完成的证明，所用数学工具，不是他那个时代具有的，于是就怀疑费马吹牛，这个理由不足，要知道缔造新工具的工具皆来自旧工具，用旧工具直接造出最新工具，不是不可能的。当然他也说过错话，但真的比假的概率大，在这个问题上相信他多点比怀疑他多点更符合数学精神。

本文发表在《数学学习与研究》2015 年第15期，2015年3月修改于深圳。后收录于 2017 年5月出版的《深圳基础理论原创文集》（数学物理卷）一书中，此文为科普版。但保留了完整的证明步骤，绝不学费马，用“我有一个巧妙证明，可惜这是科普版，没法严谨表达”来搪塞，而是既有严谨表达，又有故事叙说。多点数感，多点直觉来帮助读者理解数学形式化语言。

1. 整数的幂尾数在4数周期内循环

考虑到洛书的数独图所呈现出来的幂尾数体现了4周期规律，故把这一发现命名为洛书定理，就像不同模数不同余数的未知数可用孙子算法解决于是叫孙子定理一样，尽管现代算法是独立发现的，我们还是要尊重古人的首次发现权。

那洛书定理的现代数学表达是怎样的呢？ 用模运算表达就是：

偶数的情形（2 幂数左旋，8 幂数右旋）： （2mod10）n ≡（2 or 4 or 8 or 6）mod10； （8mod10）n ≡（8 or 4 or 2 or 6）mod10； （4mod10）n ≡（4 or 6 or 4 or 6）mod10； （6mod10）n ≡（6 or 6 or 6 or 6）mod10； （0mod10）n ≡（0 or 0 or 0 or 0）mod10。

奇数的情形（3 幂数右旋，7 幂数左旋）： （3mod10）n ≡（3 or 9 or 7 or 1）mod10； （7mod10）n ≡（7 or 9 or 3 or 1）mod10； （9mod10）n ≡（9 or 1 or 9 or 1）mod10； （1mod10）n ≡（1 or 1 or 1 or 1）mod10； （5mod10）n ≡（5 or 5 or 5 or 5）mod10。

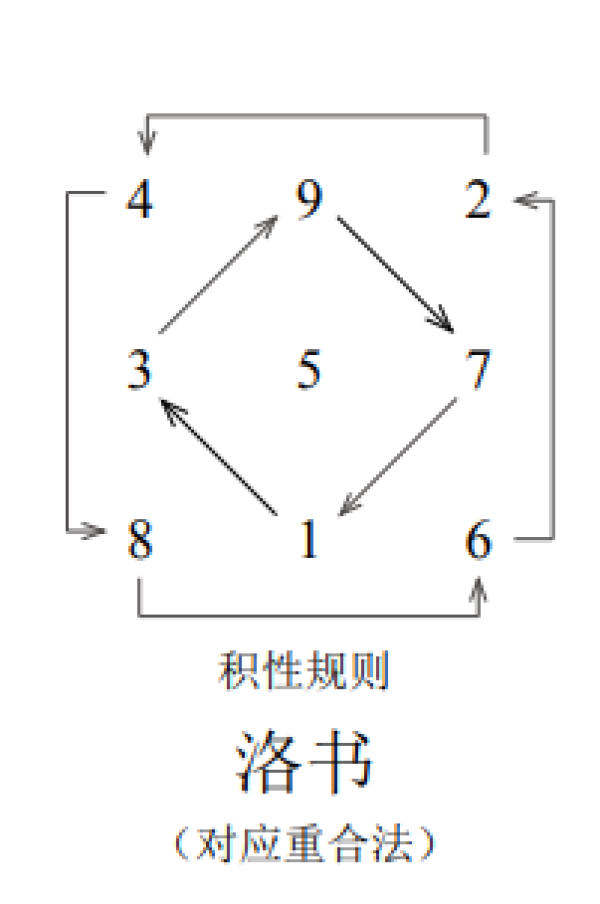
证明该定理很容易，根据乘法口诀表，我们进行排列组合得到：5 为个位 数的奇素数只有 5 一个，其他 5 为个位数的正整数都能被 5 整除。由于除 2 外 的所有素数都是奇数，所以奇素数的个位数就只能是 3、9、7、1，所有奇合数 与奇素数都是奇素数或自乘或互乘的结果，故奇数的幂数尾数除 5 外，是 3、9、 7、1，偶数的幂数尾数除 0 外，剩下的是 2、4、8、6。即所有整数的幂尾数都在4数周期内循环。

有了以上洛书定理的发现，就可以用来证明费马猜想、考拉兹猜想以及比尔猜想了，后两个猜想这里暂且不表。

2. 幂尾数周期判定法 

费马大定理虽然已经被怀尔斯所证明，但不是最简洁的证明方法，有130页。该定理断言：整数域方程 x^n +y^n = z^n ，当n ＞ 2 时，不存在正整数解。表述跟哥德巴赫猜想一样都很简单，但难住了世人 350 多年。现用最简洁的方法进行证明。

数学家发现，1 指数的费马方程有任意整数解，而当 x，y，z 互质且三元解中含5因子时，存在毕达哥拉斯（Pythagoras）③整数方程即2指数时的费马方程有整数解；三元解中都不含5因子时，存在毕达哥拉斯整数不等式：

z ^2 ＜ x^ 2 +y^2 或 x^ 2 +y^2 ＜ z^ 2

整数域毕达哥拉斯方程 x ^2 +y^2 ＝ z^ 2 ，存在本原解（核心解，即三元互质时的解）。其他解都是核心解乘任意公因数。

方程的本原解（核心解）必须满足：

 gcd（x，y，z）=1，gcd（x，y）=1，gcd（x，z）=1，gcd（y，z）=1。

方程的互质解必须满足：左边2项和右边 1 项中必有且仅有一项为偶数，因为奇数的n次方还是奇数，偶数的n次方还是偶数。方程必须左边一偶，右边一奇加一奇，或者左边一偶，右边一奇减一奇，且相互之间互质，即毕达哥拉斯方程和费马方程若有互质解必须 x，y，z 两两之间互质。

当各元指数 n=4k+2 或 4k+4 时，一奇一偶相加相减可得到5因子奇数或一奇一奇相加相减可得到5因子偶数，5因子数只有5结尾数或0结尾数。

指数为偶数2k+2时的费马方程一奇一奇的9、1尾数相加减或一奇一偶的9、 1 和 4、6 相加减都不会获得指数为 2 的同余数 9、1 和 4、6，只能获得指数为 2 的同余数0和5。若有解必有一元解含5t因子数，t 为正整数。而在 5t 因子数仍无解，则方程就无解。

指数为偶数 2k+4 时的费马方程一奇一奇的1尾数相加减或一奇一偶的1和6 相加减都不会获得指数为4的同余数1和6，只能获得指数为4的同余数0和5。若有解必有一元解含5t因子数。而在5t因子数仍无解满足等式，则方程就无解。

综合指数 4k+2 和指数 4k+4 的情形，偶指数的费马方程若有解必须有一项 拥有5t解，若无5t解则无通解。这是偶指数费马方程定理。若有解存在模形式（拥有5t解），若无解不可模形式。前者类似谷山-志村猜想的一类特例，后者类似弗赖猜想的一类特例。这个类型特例就是幂尾数周期律。下面将从幂尾数周期律出发，深挖出本原解约化律。

3. 不等式维度升降法 

那 5 因子数的本原解在毕达哥拉斯方程中存在，在指数大于2的费马方程中是否继续存在呢？ z 和 y 不取 5t 时毕达哥拉斯方程已证，都是不等式。即方程 x ^2 +y^2 =z^2 或者 y^2 –x^2 =z^2 在没有5因子数的两组解时，一定是不等式，刚已完成证明。毕达哥拉斯方程是二次方的费马方程，当指数更大时，5t 解能否继续存在？我们在毕达哥拉斯有解方程 3^2 +4^2 =5^2 或者 13^2 –12^2 =5^2 或者 20^2 +21^2 =29^2 的基础上进行分类。总的来说有以下四种代表形式：

第一种“奇减偶”等于5尾数的；第二种“奇加偶”等于5尾数的；第三种“奇减奇”等于0尾数的；第四种“奇加奇”等于0尾数的。那就在以上四种情况下递增指数，看是否还存在 5t 解，以下进行分析证明。

第一种和第三种情况。当 t 是奇数时，是第一种“奇减偶”等于 5 尾数的情况；当 t 是偶数时，就是第三种“奇减奇”等于 0 尾数的情况。现将 y ^2 –x^2 =（5t）^2 ，在真实有解等式的两边同时乘以 5t，得到： y^ 2（5t）–x^2（5t）=（5t）^3 。 此时 5t 是毕达哥拉斯方程的非互素解，要变成互素解，就得将左边的两项 5ty^2 ，5tx^2 进行更换。 5ty^2 因子项的底数变大，5tx^2 因子项的底数也同时变大，都大于 5t，那么 方程就变成了不等式。 5ty^2 因子项的底数变大于 5t，5tx^2 因子项的底数也同时变小于 5t，那么左边会更大。 将 5ty^2 因子项的底数变小，5tx^2 因子项的底数也同时变小，都小于 5t，那么方程就变成了不等式。 5ty^2 因子项的底数变小于 5t，5tx^2 因子项的底数也同时变大于 5t，那么左边会更小。总之在此基础上方程两边要获得增加的互素因子，就只能得到不等式。

因为更换办法只有四种选项，皆导致不等式的产生，不更换则不可能是互素解，  即（5t）^3 ＞ y ^3 –x^3 或 y ^3 –x^3 ＞（5t）^3 。不更换方程三元非互素没有本原解；更换吧，方程又变成了不等式。

另外两种情况，将（5t）^2 =y^2 +x^2 两边乘以 x（其中x ＞ 1），得： xx^2 +xy^2 =x（5t）^2 变换后得： xx^2 =x（5t）^2 –xy^2 要使方程互素，右边 5 因子项中的 x，以及右边 y 因子项中的 x 就要换成互素数，而一换，等式就被破坏。 y和5因子项中的x都变大，右边两项的和就变大，或者5因子项中的x变大， y 中的 x 变小，相减后趋大，故会得到（5t）^3 –xy^2 ＞ x ^3 ，不等式成立。

再看不等式方向相反的另一种情况： y和5因子项中的 x 都变小，或者 5 因子项中的 x 都变小，y 项中的 x 变大， 故会得到 x^ 3 ＞（5t）^3 –xy^2 ，不等式成立。即不等式（5t）^3 ＞ y ^3 +x^3 或 y ^3 +x^3 ＞（5t）^3 都是成立的。不等式成立，意味着原方程无整数解。本原解 5t 也不能满足等式要求。

当无5t 解时，根据 x^ 2 +y^2 ＜ z^2 或者 y ^2 –x^2 ＜ z^ 2 ，同理的方式可证明：当无5t解时，不等式升幂后 x^ 3+y^3 ＜ z^3 或者 y ^3 –x^3 ＜ z^ 3仍成立。前一个两边乘以y，后一个两边乘以x，即其中一项升幂，其它两项增减更换后升幂，因大边换大仍大，小边换小仍小，故升幂后不等式仍成立。故2次方的三元不等式，升幂后所得到的3次方的三元不等式仍成立。

于是乎得到重要结论：若有 5t 解，指数为3时的费马方程定无整数解，若无 5t 解，指数为3时的费马方程亦定无整数解。

用数学归纳法继续证明，推广到指数为 n 时也成立。 假设不等式（5t）^n ＞ y^ n +x^n 或 y^ n +x^n ＞（5t）^n 成立； 即指数 n>2 时费马方程没有5t 解；那么（5t）^（n+1） ＞ y ^（n+1） +x^（n+1）或 y ^（n+1） +x^（n+1） ＞（5t）^（n+1）也是成立的。

假设不等式（5t）^n ＞ y^ n –x^n 或 y^ n –x^n ＞（5t）^n 成立； 那么（5t）^（n+1） ＞ y ^（n+1） –x^（n+1） 或 y^（n+1） –x^（n+1） ＞（5t）^（n+1） 也是成立的。 以下证明之。

将不等式（5t）^n ＞ y^ n +x^n 的两边乘以5t，右边的两项5t 换成非5尾数较小量的 y 和 x，不等式仍成立，即（5t）^（n+1） ＞ y ^（n+1）+x^（n+1） 成立。 将不等式 y^ n +x^n ＞（5t）^n 的两边乘以 x，左边的 y 项换成较大量，5t 换成较小量，不等式仍成立，即 y^（n+1）+x^（n+1） ＞（5t）^（n+1）成立。

将不等式（5t）^n ＞ y^ n – x^n 的两边乘以 5t，右边两项 y 和 x 中的 5t 换成非5尾数的较小量，不等式仍成立，即（5t）^（n+1） ＞ y ^（n+1） – x^（n+1） 成立。

将不等式 y^n – x^n ＞（5t）^n 的两边乘以 y，左边的 x 项换成较小量，5t 换成小量，不等式仍成立，即（5t）^（n+1） ＞ y ^（n+1） – x ^（n+1） 成立。

以上费马方程5t及其他解导致不等式产生的四种可穷分类情形皆证明了迭代递推命题成立。加上费马方程指数 n=3 时无5t及其他整数解的首项判定成立， 故费马方程无 5t 及其他解的命题得证。

而用幂尾数周期判定法已证，无5t解在偶指数费马方程中必无通解，加上刚已证有5t解则偶指数费马方程会变为不等式，即大于2的偶指数费马方程一定无解。

于是现在假设大于2 的 n 指数时成立，递推项 n+1 指数时就有两种情形： 一是看奇指数2k-1 时是否成立； 二是看偶指数2k时是否成立。

奇指数 2k-1 可迭代求证出（2k-1）+1时成立，因为2k是偶指数，已证是成立的； 偶指数2k可迭代求证出 2k+1时也成立，即偶指数通过不等式维度升降可 变换为奇指数，故可知偶指数时的递推也是正确的。

不等式维度升降法的原理是，不等式的大边乘以较大量，小边乘以较小量，不等式仍成立，只是在多项式中添加了一个小小技巧，就是用不等量替换等量，不等式关系仍成立。如此得到 next 项也成立的数学归纳法递推证明，才使大于 2 的 n 指数时费马方程没有通解成立。

奇偶两者合并，即指数大于 2 时的正整数域都无整数解。这就证明了指数大于 2 的费马方程无整数解是成立的。费马猜想中的幂指数表明这是一个有序列集合概念的命题，可用数学归纳法证明，因为序列集合概念，可抽象出全称普遍概念。每递增一个指数都映射一个空集解，符合递推法则。

4. 费马当年可能完成的巧妙证明 

其实费马的无穷递降法就是数学归纳法，费马曾经用它来证明指数为 4 时方程无解，欧拉也利用无穷递降法来证明指数为3时方程无解。无穷递降法不仅可用于证明局部命题，还可以用于证明全局命题。用假设来推导命题无穷递降，直到与初项 n=4 时相符。其中初项 n=4 时可按费马的思想巧妙地证明方程无整数解成立，总之用他的体系证明费马猜想是绰绰有余的。他证明指数为 4 时的费马方程成立其实方法很多，以下就是他有可能使用的证法。

根据费马小定理 a ^（p-1） =1（mod p），必存在 w^4 +w=5^m，w与5互素，即 w ^（5-1）=1mod5，而指数为4的费马方程是 x^ 4 +y^4 =z^4 。

方程右边一个模 5 余 1， 方程左边两个模 5 余 1， 左边合并就会模 5 余 2，5 乘以任意整数都不会尾数得 1，于是方程左右矛盾，可见指数为 4 的费马方程不是等式，而是不等式。

从而证明了：指数为 4 时的费马方程无整数解。 当然其中一个不互素时，可能存在 5 因子解，但前文已证，此时会变成不等式。根据费马小定理和欧拉定理a^Φ（n） =1（mod n），还可以证明更多的偶指数费马方程无整数解。

可见从别的角度使用洛书定理，也可以得出指数为4的费马方程无整数解。至于推广到n维成立，费马则借助了无穷递降法。可见费马小定理加无穷递降法就能证明费马猜想成立。初项成立，最为关键！

费马的无穷递降法是这样反证的：假设指数为n的费马方程有整数解，因为高维有整数解那低维就定有整数解，高维无整数解那低维不一定无整数解，故指数为 n-1 的费马方程也就当然有整数解，理由是指数为n时有解，那么定有匹配的解集｛x ^n ，y^ n ，z^ n ｝和指数为 n-1 的费马方程必有整数解，如果没有， 添上解集后，使用不等式升降变换⑤（当年的费马应该懂得该方法），n 维的费 马方程就成不等式，故可反证降低 1 维后的费马方程仍有整数解。 继而指数为 n-2 的费马方程也有整数解，最后可递降到指数为 4 时的费马方程，也有整数解，但这一结果与指数为 4 的费马方程无整数解相矛盾，可见 原初假设有问题。故指数 n 不小于 4 的费马方程皆无整数解就得证。至于指数 为3的费马方程情形，可补充继续证明。 指数为3时是欧拉完成的，也是按费马的无穷递降法完成证明的。大致思路如下。

现证明 x ^3 +y^3 ＞ z^3 或 z^ 3 ＞ x^ 3 +y^3 是成立的不等式。把小自然数 1 到 10 代入 到不等式穷举成立，再假设 z=c 时不等式是成立的，可推理得到： x^ 3 +y^3 ＞（c-1）^3 也是成立的 因为不等式的小边变更小，不等式仍成立。

可再假设 x=a 时 z^ 3 ＞ a^3 + y^3 是成立的，可推理出： z ^3 ＞（a-1）^3 + y^3 也是成立的 因为不等式的小边变小，不等式仍成立。故如此无穷递降下去都是不等式， 故原方程无整数解。 还可以假设 z=c 时费马3次方程有解是成立的，然后证明 z=c-1 时费马3次方程也是成立的，因为根据奇偶性有无 2 因子可推理得到 x^ 3 +y^3 =（c-1）^3 也是成立的，因为： c 是奇数，（c-1）就是偶数；c 是偶数.（c-1）就是奇数。

奇数时有解，可推理出偶数时也有解，可添加偶数共因子； 偶数时有解，可推理出奇数时也有解，可消去偶数共因子。

由此可无穷降维下去也应成立，但与小自然数如 1、2、3、4、5、6、7、8、9、 10…等代入费马方程中的z 经过验算无解而发生矛盾，因为在三维时，左边两加项的原二维素因子域，虽有解但增维后会扩展素因子，但右边无素因子可增， 而本原解方程要求三元互素，导致 z 无可互素的素因子，即不可模表示，故费马方程 3 次方时是不等式。一般无穷递降法多半使用反证法，证明假设无穷递降后会与初项矛盾。难怪欧拉证明完费马3次方程无解后就撒手不继续干了，因为证明其他维度的费马方程无解都可如法炮制。

指数为 2 时，不等式就不成立，首先穷举小自然数时有例外，故递推自然数时即便没有矛盾也枉然。以上完成了针对底数的无穷递降法后，就可以继续针对指数也实施无穷递降法的证明。

数学归纳法是针对自然数做变量而生效的，不论自然数映射的对象是单个元素还是一群数集，都是可行的。费马方程指数为 3 指数为 4 时无整数解已证，现假设指数为 n 时方程也无整数解，就可以递推到指数 n-1 时费马方程亦无整数解，递推方法依然是无穷递降法。

当 y^n + x^n ＞ z^ n 或 z^ n ＞ y^n +x^n 为不等式成立时： 由 y^（n-1） + x^（n-1） ＞z^（n-1）可知，不等式的小边消去一个较大因子，不等式小边仍小。 由z^（n-1） ＞ y^（n-1） + x^（n-1） 可知，不等式的大边消去一个较小因子，不等式大边仍大。

也就是说假设高维费马方程有解，可递推到低维费马方程有解，故矛盾， 由此可推理出费马方程指数不小于 3 时无整数解。即假设： y^n +x^n =z^n 或 z^ n = y^n +x^n 为费马方程成立时，可得到： y ^（n-1） +x^（n-1） =z ^（n-1） 它由原方程消去一个内积向量（x，y，z）而得到，其基础解系方程仍成立， 由 z^（n-1） = y ^（n-1） +x^（n-1） 可知，降维的基底方程仍然生效有解。但这会与费马方程三维四维无解矛盾，故假设不低于三维的高维费马方程有解是不真的，费马猜想获证。之所以无穷递降就是为了同低维的结论产生矛盾。而一般数学归纳法是无穷递增的，其实数学归纳法也包含无穷递降，两者是相容的。两者都体现了相邻论的思想。

可相邻递推再加初项成立是标准数学归纳法，不等式降维升维可帮助相邻递推，无穷递降法直接加初项不成立是归谬数学归纳法，因为无穷递降法是远邻递推，二者都需要初项成立或不成立。也就是说必须要证明，费马方程指数为 4 时无整数解，我不知道费马是如何证明指数为 4 时方程无整数解的，也不知道欧拉是如何证明指数为 3 时方程无整数解的。但我知道，他们的思路是正确的。 一般来说，直推时多用数学归纳法，反证时多用无穷递降法。

高维肯定为真可推得低维肯定为真； 低维否定为真可推得高维否定为真。 反之则不可逆推，要逆推也须基准条件注明，即低在哪个度，高在哪个度。不能因为费马猜想四维成立就可用无穷递降法来证明三维也成立，四维成立， 是无穷递降法证明费马猜想成立时所必须用的初项，三维不在范围内，故不可递推，须另外证明。欧拉把指数无穷递降换成底数无穷递降就可证明三维的费马猜想了。欧拉的三维原版证明是否如此不得而知，我所知有限，估计也就递推项的证明不一样，但我知道欧拉的大体思路一定是这样的。命题与假设不矛盾（通过不等式维度升降法），其次用洛书定理或费马小定理证明了使用归纳法时必须要的命题初项成立（通过幂尾数周期循环法）。 而费马是从指数 4 时无解直接用无穷递降法后继相邻归谬证明了费马猜想，这是可行的，只是比较抽象而已。在证明后继相邻成立时，用到了本原解乘以或 除以 2 的幂集数可扩充得到通解，使奇偶数可成功相互变换成立，把乘性问题变成加性，把加性问题变成乘性，这是成功证明的关键。即：

c=2^k·a 为偶数时可推得， c-1=a 为奇数。 

从费马方程中的偶指数大于2无解出发，获得了不等式降维变换的证明。

已知，在正整数域中，A^2 +B^2 ＞ C^2 或者 A^2 +B^2 ＜ C^2 ，求证，A+B ＞ C 或 者 A+B ＜ C 亦成立，其中费马方程中的变量偶指数大于 2。

证明： （1）当 A ＞ B ＞ C 时，则 A+B ＞ C；

（2）当 A ＜ B ＜ C 时，则 A^2 /C+B^2 /C ＞ C^2 /C 大边的分母变小时大边仍大，小边的分母变大时小边仍小。 于是，A^2 /A+B^2 /B ＞ C^2 /C，可得，A+B ＞ C。

（3）当 A ＞ B ＞ C 时，则与 A^2 +B^2 ＜ C^2 无关；

（4）当 A ＜ B ＜ C 时，则 A^2 /C+B^2 /C ＜ C^2 /C 大边的分母变小时大边仍大，小边的分母变大时小边仍小。 于是，A^2 /A+B^2 /B ＞ C^2 /C，可得，A+B ＜ C。

（5）当 A ＞ C ＞ B 时，则与 A^2 +B^2 ＜ C^2 无关；

（6）当 A ＜ C ＜ B 时，则 A^2 /A+B^2 /A ＜ C62 /A 大边的分母变小时大边仍大，小边的分母变大时小边仍小。 于是，A^2 /A+B^2 /B ＜ C^2 /C，可得，A+B ＜ C。

（7）当 A ＞ C ＞ B 时，则有 A^2 +B^2 >C^2 ，且有 A+B>C；

(8) 当 A ＜ C ＜ B 时，则定有 A+B ＞ C。

而 A 项与 B 项满足交换律，无须重复考虑，于是 ABC 三元大小分布的情形均已囊括，皆可推得降维后的不等式成立，即 ABC 三元偶指数方程无整数解时，大于 2 时的奇偶指数方程亦无整数解。

根据偶数 s=2^k· t，可推得奇数 c-1=t，且 t 为奇数，既然偶指数情形存在不等式，那么2t 指数情形就自然存在不等式，则由 x ^2a +y^2a =z^2a （a为正整数）降维得到的奇偶指数方程亦无整数解。即根据（x^ t ）^2 +（y ^t ）^2 =（z^ t ）^2 无整数解成立， 可推得奇指数时 x^ t +y^t =z^t 无整数解成立。亦可根据（x ^a ）^2 +（y^ a ）^2 =（z^ a ）^2 无整数解成立，可直接推得大于 2 的正整数指数时 x ^a +y^a =z^a 无整数解成立。也就是说，费马方程大于2的奇指数以及正整数指数的情形皆得证无整数解。

这个证明真的显示了，费马当年只要《算术》一书边角稍微大一些，就可书写完毕“他的证明”，因为可用证明的文字的确不需要很多。用幂尾数周期判定法以及不等式维度升降法，作者完成了此项证明。而该方法一定在费马时代有同物而异名的等价表达，费马小定理、不等式降维变换与无穷递降法就是。无穷递降法和无穷递进法都是数学归纳法，它通过远邻递推出结果与初项或矛盾或不矛盾，代替数学归纳法中的用相邻递推出结果与假设不矛盾，再加初项 成立来证明命题。两者的核心方法是一致的，本文的证明用的是后者，费马完全具备可证明的条件。故费马有一个巧妙证明是完全可能的，书角写不下，两三页纸还是可以写完的。

而怀尔斯的证明非常复杂，其思想是，有解的椭圆曲线方程一定是可模形式的，这就是谷山-志村猜想，这一点被怀尔斯所证明，而弗赖曲线是不可模形式的，由肯.黎贝证明，就像费马方程曲线，怀尔斯进一步通过证明 E- 序列与 M- 序列有一一映射的关系，继而反证，如果不可模形式的费马方程有解，就会同可模形式的谷山-志村猜想相矛盾，于是费马猜想得证。这是怀尔斯的证明。仔细想了下，它同本文证明还是有些相似的，幂尾数周期判定法与模形式有某些相同的功能，而不等式维度升降法与序列映射证明可递推出一样的目标。谷山-志村猜想就像毕达哥拉斯方程必有解是可模 5p 与 0 同余的。

同130多页的论文相比，本文的证明更加简洁，就现代化的算法而言，本文的工具更加朴素，但都打开了通往未知世界的大门。

另外，本文作者还通过证明 ABC 猜想证明了费马猜想、比尔猜想，见本书《揭示 ABC 猜想的反直觉之谜》一文。而 ABC 猜想又是通过哥德巴赫猜想完成证明的，反之不可，可见哥猜是更强命题。

5. 书边角宽点真能写下费马猜想的证明

书边角宽点真能写下费马方程无整数解证明：

5.1现假设费马方程指数为给定数 n＞0 时无本原解，可证 x^ (n+1)+y^ (n+1)=z ^(n+1) 必无整数解，根据 x^ n +y^ n =z^ n 无整数解，即无基础解系，它的特征值正交基映射（x，y，-λ）必无解，即 x^( n+1)+y^( n+1)=λz^n 必无解，当然取特征值 λ=z 时也必无解。再证用不含特征值也不含匹配数的向量组来内积递增指数所得到的 next 项命题也成立（即完成高阶数学归纳法中的递推部分证明），这种情形属于不等式变换，三元一次不等式，乘以正数不等式不变，乘以负数不等号反向（本原解与通解变换），乘以特征值或匹配数以及所对应的向量组，除勾股方程外，其他不能做到双向数值匹配（保持非互素），故不等式仍成立（基础解系与通解变换），大边乘以或替换绝对值大量，小边乘以或替换绝对值小量，不等式关系不变（纯不等式变换）。

5.2.假设指数给定数 n ＞ 0 时费马本原解方程有解，即存在三元一次方程有解，毕达哥拉斯方程有解，可证 x ^(2+1)+y^ (2+1)=z^ (2+1) 必无解，即毕氏方程有 5t 解或1次方程有解时，x^ 3 +y ^3 =z ^3 无整数解(两种有解情形都是毕氏方程的升幂1次方)，从而证明了费马方程无解的初项成立。费马方程指数 n=1，2 为无解情形时，必 x ^3 +y^ 3 =z^ 3 无整数解（非互素线性组合的匹配数性质）。1 次方或2 次方任意一组有解情形时，升幂后所得到的 x^ 3 +y^ 3 =z^ 3 必无整数解（非互素线性组合的特征值性质），两组为有解情形时，x^ 2 +y^2 =z ^2 ，两边乘以z，得 zx^2 +zy^2 =z^ 3 ，因为 z＞y＞x 是定义条件，且三元线性相关，故用大变小替代原表达后，得 x^ 3 +y^ 3 ＜ z ^3 ，故原方程无解，这是改用互异递推条件导致互素的（不等式变换性质）。这样费马方程指数大于 2 的初项命题3次方时被证成立，加上递推得到的 next 项必成立（5.1已经完成递推证明）。于是费马方程无整数解获证。

这里的本原解对应可模形式，高维不可模形式可递推低维不可模形式对应弗赖猜想（肯.黎贝定理，相当于5.1），也可对应它的逆否命题，低维可模形式可递推高维可模形式，而相对高维可模形式亦可递推低维可模形式，对应谷山-志村猜想（怀尔斯定理，相当于5.2），费马猜想无解证明的递推部分是肯.黎贝定理完成的，费马猜想无解证明的初项或低维部分是怀尔斯完成的，低维不可模形式可推出相对高维不可模形式，是1次方和2次方的两类可模形式升幂的结果，恰好升到3次方时，破坏了模形式，推出了首个相对高维的不可模形式，从而给递推证明准备好了初项成立的条件。这个可直觉理解并可简单证明的问题，怀尔斯是通过复杂手段解决的，大多数人都无法直觉理解。根据奥卡姆剃刀原则，本文作者的证明更具合理性。费马完成了4次方时的无解证明，只差没有合理交代这是高阶数学归纳法的初项，以及无穷递降法的递推部分证明，怀尔斯的功绩在于完成了这个可递推的初项表达，与高阶数学归纳法关联了起来，递推部分可借助肯.黎贝定理。

怀尔斯和肯.黎贝所完成的事情，费马也是可对等做到的，不妨来对接下费马在那个时代已掌握的数学工具，不等式和方程升幂变换，那个时代早就会，所以无穷递降法的递推不是问题，甚至高阶数学归纳法也定是会用的；另外费马完成3次方时的无解证明也不是难事，欧拉的证明就是学习费马的方法完成的，因此费马完全有可能完成过费马猜想的正确证明，至少是具备思路可行的正确证法。（文/罗莫）

参考文献 :

[1] 罗莫 . 用河图洛书原理破解了考拉兹猜想 [J]. 数学学习与研究，2012 （11）：115-116.

[2] 西蒙·辛格 . 费马大定理：一个困惑了世间智者 358 年的谜 [M]. 薛密， 译 . 桂林：广西师范大学出版社，2013.

 [3] 范德瓦尔登 . 代数学Ⅰ [M]. 丁石孙，孙肯成，郝鈵新，译 . 北京：科 学出版社，2009.

 [4] 迪克森 . 代数方程式论 [M]. 黄缘芳，译 . 哈尔滨：哈尔滨工业大学出 版社，2011.

注释：

 ①洛书定理，割余法的一种，任何一个自然数都可以分割成用模数和余数表达的算式，其中用模数作为底数以任意自然数为指数所得到的值作为假余数， 由此洛书定理发现，偶数可以无漏表达成 2a+2^k ，奇数可以无漏表达成 3b+2^t ， 而这正是考拉兹猜想的等价表达。

 ②比尔猜想，提出这一猜想的是得州银行家 D . 安德鲁，该猜想比另一个与之相关的数学难题“费马最后的定理”更难解决。美国数学协会 2013 年 6 月宣布，任何人只要能给出比尔猜想数字理论的解决方案， 比尔就会奖励给这个人 100 万美元。

 ③安德鲁 • 怀尔斯，英国著名数学家。他于1995 年证明了数论中历史悠久的“费马大定理”，并由此在 1998 年国际数学家大会上获得了国际数学联盟特别制作的菲尔兹奖银质奖章。怀尔斯现在任教于英国牛津大学。

 ④毕达哥拉斯（约前 580 年－约前 500 年），古希腊哲学家、数学家和音乐理论家。他是传统上所知的勾股定理（又称毕达哥拉斯定理）首先发现者。

 ⑤不等式升降变换。不等式指数增减等价变换，不等式关系满足指数的迭代推演，低指数时不等式成立，高指数时不等式仍成立，不等式大边更大，小边更小时，不等式仍成立。